基于遗传算法三轴磁传感器校正系数求解

庞学亮，林春生

(1.武汉工程大学，湖北 武汉 430205；2.海军工程大学，湖北 武汉 430033)

基于遗传算法三轴磁传感器校正系数求解

庞学亮1，林春生2

(1.武汉工程大学，湖北 武汉 430205；2.海军工程大学，湖北 武汉 430033)

针对三轴磁传感器校正模型系数之间存在较强相关性，提出了基于遗传算法三轴磁传感器校正系数求解方法。该方法能不考虑地磁场短时变化，构建目标函数，初始种群根据适应度进行交叉、变异操作，逐步淘汰差的个体，得到最适应目标函数的最优解,够很好地克服系数之间的相关性，对校正模型系数具有很高的估计精度；数值仿真结果表明，该方法可以稳定地收敛并可以达到很高的参数估计精度。

三轴磁传感器；校正系数；遗传算法

0 引言

三轴磁传感器指磁通门矢量磁传感器，具有体积小、精度高、抗冲击性能好等特点，在地磁导航、航空磁探、水下平台磁场测量等需要磁场测量场合，经常会采用三轴磁传感器进行标量测量。可是由于加工工艺等原因，三轴磁传感器三轴很难做到完全正交，同时三轴也存在一定差异，接收器电路存在漂移、噪声，接收器铁芯存在剩磁，数据采集存在截断误差等，这就给测量带来两方面影响：1)由于地磁场的存在，当传感器姿态发生变化时，在相对稳定的地磁场下，其标量输出也不是一个稳定的值，产生很大干扰信号；2)由于三轴已经偏离了正交，致使按照理想情况进行计算的标量值也产生了偏差[1-2]。这就需要对三轴磁传感器进行校准，目前校准的思路是先建立三轴磁传感器信号输出模型，通过在稳定地磁场下测量的数据求解模型系数，然后再根据模型系数进行输出信号校准。三轴磁传感器校准的关键是校准模型精度和模型系数的求解，对于校准模型通常考虑三轴正交性、灵敏度一致性和剩磁三个因素，而模型系数求解的方法有很多种，比如极大似然方法校准方法[3]，支持向量回归(Support Vector Regression)方法进行校准[4]，非线性最小二乘法参数估计[5]，共轭梯度法进行系数求解[1]，模型系数自动搜索方法[6]，自适应系数求解法[7]。归纳起来这些方法对模型参数估计都有一定的效果，但由于模型系数之间存在一定相关性，这些方法很难保证模型系数的求解精度，也缺乏对实际补偿效果的验证[8-10]。

遗传算法(Genetic Algorithm)是一种基于达尔文进化论的非梯度并行优化算法，它广泛的用于非线性、非连续、非凸、多模态问题优化，具有很强的全局最优点寻找能力[11-12]；本文根据遗传算法特点，提出采用遗传求解三轴磁传感器校正模型系数的方法，以克服模型系数之间的相关性。

1 三轴磁传感器校正模型

三轴磁传感器标量输出误差主要来源于三轴正交误差、三轴灵敏度误差和三轴剩磁，为了建立三轴磁传感器校正模型，首先建立三轴磁传感器坐标系。磁传感器的三个轴坐标分别为X、Y和Z，其输出信号分别为BX、BY和BZ；正交坐标系XO、YO和ZO，外磁场在正交坐标投影分别为BXO、BYO和BZO，正交坐标系和三轴磁传感器坐标满足以下关系：1)ZO轴与Z轴重合；2)坐标面YOZ与YOOZO共面，并假设OY轴与OYO轴夹角为β，X轴与XO轴夹角为λ，与ZO的夹角为π/2+α，与YO轴夹角为π/2+γ。如图1所示。

只考虑三轴不正交影响，三轴磁传感器每个轴的输出外磁场三个分量在传感器该轴上投影的和，用BX、BY和BZ表示，三轴的输出表示为：

实际三轴磁传感器很难保证三轴完全正交，但是其误差可以控制在1°以内，角度参数λ、α、γ和β为小量，根据泰勒展开，忽略高阶小量，做近似处理，cosλ≈1，cosβ≈1，sinγ≈γ，sinα≈α，sinβ≈β，三轴磁传感器输出简化为：

考虑灵敏度不一致，忽略线性度不一致性，假设三轴的灵敏度分别为kX、kY和kZ；考虑三轴磁传感器铁芯剩磁和电路的漂移，假设剩磁和电路漂移为恒定值，分别用ΔBXO，ΔBYO和ΔBZO表示，三轴磁传感器输出表示为：

令a11=kX(1-λ2/2)，a12=kXγ，a13=kZα，a22=kY(1-β2/2)，a23=kYβ，a33=kZ，根据可以得到正交坐标系三轴磁传感器输出矩阵形式：

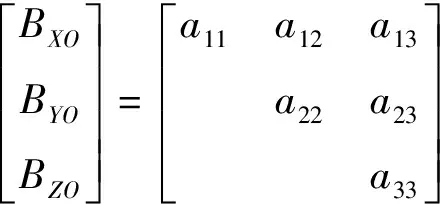
或表示为BO=A-1·(B-ΔBO)，根据该公式，可以得到正交坐标系外磁场的三个分量，通过该公式可以实现三轴磁传感器非正交、灵敏度和剩磁影响的校正，对此需要求解出模型系数，该模型含有9个参数，但在实际校正时，需要已知地磁场模量，因此，校正模型的系数总共有10个，只要准确求解出这10个系数就可以对三轴磁传感器进行校正。

2 基于遗传算法校正系数求解

遗传算法(GA)其基本思想是基于Darwin进化论和Mendel的遗传学说，它吸取了自然界的自然选择、适者生存以及遗传、变异等思想，从一组初始解开始迭代，逐步淘汰较差的解，产生更好的解，直到满足某种收敛指标为止，即得到了问题的最优解[13]。

遗传算法具有多点寻优、并行处理等特点，而且遗传算法的搜索过程是从初始解群开始，以模型对应的适应函数作为寻优判据，适者生存，劣者淘汰，从而直接对解群进行操作，而与模型的具体表达方式无关，这就决定了遗传算法可适用于一般非线性系统模型的参数估计。

对于三轴磁传感器校正模型，采用遗传进行参数估计。将三轴磁传感器置于磁场均匀的环境中，短时间内认为地磁场稳定不变，已知的条件为：

根据采集数据采用遗传算法，估计模型的未知系数。具体步骤如下：

1)编码：对于模型系数Cij(i=1,2,3;j≥i，ΔBX0)、ΔBY0、ΔBZ0和C采用二进制编码；参数Cij(i=j,i=1,2,3)接近于1，Cij(i≠j,i=1,2,3,j≥i)值远小于1，ΔBX0、ΔBY0、ΔBZ0根据实际测量，其范围在50 ～500 nT之间；地磁场C可采用高精度光泵磁传感器进行实际测量，其搜索范围可以控制在±25 nT。

2)目标函数：取各个测量点校正后三轴输出的平方和与地磁场模量的差值的均值为目标函数f，适应度由目标函数确定，目标函数越大，适应度越差。

3)产生初始种群：根据参数设定范围，随机产生每个参数的二进制串。

4)计算目标函数：将各个位串解码得到各个参数，带入校正模型，得到校正后输出，根据上式计算出对应目标函数值fi。

5)交叉：根据目标函数确定适应度，进行交叉变换，产生新的个体。为了防止遗传算法过早收敛，增加搜索到全局最优解的可能性，采用改进的遗传算法，并不直接产生新的解群，将父辈和子辈都作为新一代解群的候选个体，按它们的适应值大小排列，取前一半为新一代解群。

6)变异：以一定概率在新的种群中挑出一个个体，在一随机位置进行变异。

重复4)、5)、6)步骤，直至算法收敛，适应值很难进一步提高。

3 数值仿真

为了验证遗传算法求解三轴磁传感器校正模型系数的性能，通过数值仿真产生不同姿态下三轴磁传感器输出，采用遗传算法进行系数求解。仿真假设：地磁场模量为50 000 nT，磁偏角变化为-4π～4π，磁偏角变化-π/3～π/3，假设参数如表1。

表1 参数假设值

表2为采用遗传算法求解的模型参数，其参数估计误差小于1‰。

表2 参数求解值

图3为初始种群目标函数曲线图，初始的目标函数值较大，与干扰噪声量级相当。图4为20次迭代后目标函数值。

图5为200次迭代后种群目标函数均值变化和最优解目标函数值的变化。

图6为采用求解的模型参数进行校正的效果，其模量输出干扰信号峰峰值减低至2 nT以下。

仿真过程中发现种群个体中，地磁场范围设定对参数估计精度影响很大，为了衡量地磁场范围设定对参数估计精度影响，对校正矩阵A-1参数a11估计精度进行仿真，假设地磁场值中心设定地磁场个体参数范围，参数范围从1 000 nT变化至10 nT，图7为仿真结果。

从仿真结果看地磁场范围值的设定对参数估计有很大影响，在实际校正时，可采用高精度光泵磁强计对地磁场进行准确测量，其误差可以控制在1个 nT，其参数范围根据实际测量值进行设定。

4 结论

本文提出了基于遗传算法三轴磁传感器校正系数求解方法，该方法不考虑地磁场短时变化，构建目标函数，初始种群根据适应度进行交叉、变异操作，逐步淘汰差的个体，得到最适应目标函数的最优解。数值仿真结果表明,该方法可以稳定地收敛，其校正系数求解精度远远优于其他方法；但该算法对地磁场值较为敏感，实际应用中可以采用光泵磁传感器进行地磁场测量，尽量选取地磁较为稳定的测量数据进行参数求解。

在三轴磁传感器校正模型建立中只考虑了三轴正交误差、灵敏度误差和剩磁影响，实际中三轴的非线性误差也会对校正结果产生影响，关于非线性误差校正下步将继续研究。

[1]胡海滨,林春生,龚沈光.基于共轭次梯度法的非理想正交三轴磁传感器的修正[J]. 数据采集与处理, 2003,18(1):89-92.

[2]周庆飞，汪海涛，梁斌. 磁通阀式磁传感器最小二乘校正[J]. 探测与控制学报，2009，31(2)：63-65.

[3]KokManon,DHolJeroen.Calibrationofamagnetometerincombinationwithinertialsensors[C]//15thInternationalConferenceonInformationFusion.IEEE, 2012: 787-793.

[4]Shi Jun. Adaptive Calibration Algorithm of Three Axial Magnetic Fluxgate Sensor Using Support Vector Regression[C]//2010 Chinese Control and Decision Conference, IEEE, 2010: 4222-4225.

[5]Springmann John C, Cutler Janmes W. Attitude-Independent Magnetometer Calibration withTime-Varying Bias[J].Journal of Guidance,Control,and Dynamics, 2012,35(4): 1080-1088.

[6]邱立军，林春生，傅霖宇. 基于三轴磁传感器运动噪声消除方法的系数搜索[J].海军航空工程学院学报, 2002,17(4):422-426.

[7]龙礼，张合.三轴地磁传感器误差自适应校正方法[J].仪器仪表学报，2013,34(1):161-165.

[8]Roberto Alonso, Shuster Malcolm D. Complete linear attitude-independent magnetometer calibration[J]. Journal of the Astronautical Sciences, 2003,50(4):477-490.

[9]Crassidis J L, Lai Kok-Lam, Harman R R. Real-time attitude-independent three-axis magnetometer calibration[J]. Journal of Guidance, Control and Dynamics, 2005,28(1):115-20.

[10]Gebre-Egziabher D, Elkaim G, Powell J, et al. Calibration of Strapdown Magnetometers in Magnetic Field Domain[J]. ASCE Journal of Aerospace Engineering, 2006, 19( 2): 1-16.

[11]段世忠，周荫清.应用遗传算法的频域最大似然参数辨识[J].北京航空航天大学学报, 2001,27(5)：532-535.

[12]Duan Shizhong,Zhou Yinqing.Identification of Frequencey Domain Maximum Likehood System Using Genetic Algorithm[J].Journal of Beijing University of Aeronautics and Astronautics. 2001,27(5):532-535.

[13]丁富春，张明龙.基于改进遗传算法的非线性发电机励磁系统参数辨识.继电器[J]. 2005,33(9)：27-31.

Calibration Coefficients Solving of Three-Axis MagneticSensor Based on Genetic Algorithm

PANG Xueliang1, LIN Chunsheng2

(1.Wuhan University of Engineering, Wuhan 430205, China; 2.Naval University of Engineering, Wuhan 430033, China)

According to the coefficient correlation problem of established calibration model, a methods using the genetic algorithm to solve the model coefficient was proposed. Without considering the geomagnetic field short-time change, the target function was established. According to the fitness, the difference of individual was phased out and the optimal solution of objective was obtained after crossover and mutation.Using the genetic algorithm to solve the model coefficient could overcome the correlation with high estimation accuracy.The simulation showed that this method could converge steadily and achieve high estimation precision.

three-axis magnetic sensor; calibration model; genetic algorithm

2016-08-02

庞学亮(1978—)，男，山东临沂人，博士，研究方向：军用目标特性，微弱信号检测，磁探测。E-mail:pxlwgx2002@163.com。

TM936.1

A

1008-1194(2017)01-0042-04