沥青基碳纤维热导率的间接法测量

吴 晃 叶 崇 刘洪波 刘金水 李轩科

（湖南大学材料科学与工程学院，先进炭材料研究中心，长沙 410082）

0 引言

随着电子及通讯技术的迅猛发展，电子器件的高频、高速以及大规模集成电路的密集和小型化，使得单位容积电子器件的发热量迅速增大，传统的散热材料已经不能完全满足要求，而以碳纤维作为增强体的高导热复合材料具有无可比拟的优势，可以用于电气元件及集成电路等的散热［1－4］。热导率的精确测定，对于开展高性能碳纤维的制备及其应用研究具有十分重要的指导作用。目前，碳纤维单丝热导率的测试方法主要有：直接测试法［5－11］和间接测试法［12－14］。间接测试法是指通过“四探针法”直接测量纤维的电阻值，从而算得电阻率，再通过经验公式计算得到热导率值。相比于直接测试法，间接测试法制样简单、测试周期短、效率高，已被国内外学者广泛采用［15－18］，但电阻率与热导率之间的对应关系至今尚未有一个公认的通用公式，常用的经验公式主要有以下3个：

袁观明［21］研究了不同热处理温度带状纤维的室温轴向电阻率，结果表明当热导率在600 W／（m·K）以上时，3个公式得到的值差异较大，当热导率在100～600 W／（m·K）时，3个公式得到的值比较接近。目前对于不同热导率值的碳纤维与3个经验公式适用性之间的研究尚未见报道。本文通过采用间接法测试得到商品化的6种沥青基碳纤维单丝的轴向电阻率，再代入上述3个公式计算出热导率，并与生产厂商公布的热导率值进行比较，筛选出计算值与公布值最接近的经验公式，以期为国内外同行提供一定的数据参考。

1 实验

1.1 材料及仪器设备

所使用的6种沥青基碳纤维分别为美国Cytec公司生产的K1100、P55和P25碳纤维，日本三菱化学公司生产的K13D2U和K13C2U碳纤维以及日本石墨纤维公司生产的XN－90碳纤维。仪器设备主要有英国AIM－TTI公司的数字微欧计和美国FEI公司的Helios NanoLab 600i双束电子显微镜。

1.2 试样制备及试验方法

截取一段长约100 mm的碳纤维复丝，将其放入1 L的烧杯中，倒入适量丙酮至完全浸没纤维，用保鲜膜将烧杯口包住防止丙酮挥发，浸泡6 h后取出纤维。此时，纤维表面的上浆剂已溶解在丙酮中，纤维束呈发散状更易分离出单根碳纤维。将浸泡过后的碳纤维复丝干燥后用镊子小心分离出碳纤维单丝。由于沥青基碳纤维单丝极脆，应尽量避免因损伤而导致纤维断裂。将碳纤维单丝拉直使其与银导线垂直接触，用透明胶带将纤维两端固定后再在纤维与银导线的接触部位滴上导电银胶，其中电压测试端内碳纤维的长度为25 mm。待导电银胶充分固化后，先采用数字微欧计测得待测碳纤维单丝的电阻值R，其原理图如图1所示，再用镊子将测量后的纤维单丝取下使用扫描电镜获得该纤维单丝断面的微观形貌图，然后通过图像处理软件得到单丝横截面积S，最后算得纤维单丝的轴向电阻率，将电阻率分别代入上述3个经验公式即可获得其对应的单丝的热导率。

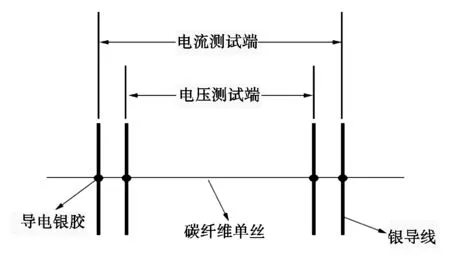
图1 微欧计测试碳纤维单丝电阻原理图Fig.1 Micro ohm test schematic

2 结果与讨论

2.1 6种碳纤维热导率的测定

图2为6种碳纤维的横截面扫描电镜图片。

图2 6种沥青基碳纤维截面形貌Fig.2 Cross section morphologies of six kinds of pitch⁃based carbon fibers

由图2（a）可知，K1100纤维截面均呈现出放射状兼具不规则劈裂的石墨微晶片层结构，纤维圆度较差。从图2（b）可看出，K13D2U纤维截面呈现出细小的褶皱辐射状石墨微晶结构，纤维直径离散性较大，部分纤维存在一定程度的劈裂现象，但整体圆度较好。由图2（c）可知，K13C2U纤维截面边缘均呈现出细小的褶皱洋葱皮状石墨微晶结构，中心为辐射状石墨微晶片层结构，纤维没有出现劈裂现象整体圆度较好，但直径存在一定的离散性。由图2（d）可知，XN－90纤维整体圆度较好，截面边缘呈现出放射状的石墨微晶片层结构，中心呈现出洋葱皮状的石墨微晶结构，部分纤维中心出现孔洞。由图2（e）和（f）可知，P55和P25碳纤维没有劈裂结构，整体圆度较好，截面边缘呈现出放射状的石墨微晶片层结构，中心呈现出平行排布的微小石墨片层结构。从6种碳纤维中分别选取20根碳纤维单丝进行截面积统计得到其离散系数分别为 13.98%、16.69%、8.36%、11.55%、19.37%和19.09%。6种碳纤维的单丝截面积离散系数都超过了8%，为了更加准确地获得碳纤维单丝轴向热导率，必须对每一根测量的碳纤维单丝进行原位截面积表征，再通过图像处理软件对碳纤维单丝的截面图进行拟合，尽可能精确测量碳纤维截面积从而用于计算碳纤维单丝的轴向电阻率。

表1为6种碳纤维的热导率［22－23］。将表1中的电阻率值分别代入经验公式（1） ～ （3）得到 λ1、λ2、λ3，其中，计算得到的K1100热导率值与美国 Cytec公司公布值的偏差分别为 0.05%、3.81%、19.56%；K13D2U热导率值与日本三菱公司公布值的偏差分别为 0.12%、5.34%、4.63%；K13C2U 热导率值与日本三菱公司公布值的偏差分别为 1.63%、8.65%、5.10%；XN－90热导率值与日本石墨纤维公司公布值的偏差分别为14.22%、23.25%、0.25%；P55 热导率值与美国Cytec公司公布值的偏差分别为7.52%、25.07%、18.08%；P25热导率值与美国 Cytec公司公布值的偏差分别为 6.87%、42.68%、96.48%。 可见使用不同的经验公式得到的热导率值差异很大，对于K1100、K13D2U和K13C2U三种热导率值＞600 W／（m·K）的碳纤维，使用公式（1）计算得到的单丝热导率值与厂商公布值最为吻合；对于XN－90这种热导率值在 300～600 W／（m·K）的碳纤维，使用公式（3）计算得到的单丝热导率值与厂商公布值最为吻合；对于P55和P25两种热导率值小于300 W／（m·K）的碳纤维，使用公式（1）计算得到的单丝热导率值与厂商公布值最为吻合。

表1 6种沥青基碳纤维的热导率Tab.1 Thermal conductivity of pitch⁃based carbon fibers W／（m·K）

2.2 沥青基碳纤维单丝热导率与电阻率函数模型

不同热导率的碳纤维适用不同的经验公式，将测得的沥青基碳纤维单丝电阻率与其热导率建成一个函数关系模型，该模型具有较强的普适性（图3）。

图3 沥青基碳纤维热导率与电阻率函数关系Fig.3 Relationship between thermal conductivity and electrical resistivity of pitch⁃based carbon fibers

从图3中可得拟合后热导率与电阻率的关系式为：

相关系数R＝0.9964，表明拟合函数与测得数据相匹配。表2为使用式（4）算得的纤维单丝热导率值。

表2 沥青基碳纤维单丝的热导率及其偏差Tab.2 Thermal conductivity and deviation of individual pitch⁃based carbon fibers W／（m·K）

从表2中可以看出，使用公式（4）算得的沥青基碳纤维单丝热导率值与其厂商公布值比较接近，偏差都在10%以内，表明公式（4）适用于沥青基碳纤维单丝热导率的计算。

3 结论

通过对 K1100、K13D2U、K13C2U、 XN－90、P55及P25六种商品化的沥青基碳纤维进行测试分析可知：对于热导率值＞600 W／（m·K）的沥青基碳纤维应选用Zhang X的经验公式即λ＝1261／ρ较为合适；对于热导率值在300～600 W／（m·K）的沥青基碳纤维宜选用 Lavin的经验公式即 λ＝440 000／（100ρ＋258）－295；对于热导率值＜300 W／（m·K）的沥青基碳纤维应选用Zhang X的经验公式即λ＝1261／ρ较为合适。将测得的沥青基碳纤维单丝电阻率与其热导率数据进行拟合得到 λ＝152 740／（100ρ＋22）－26，具有更强的普适性。

［1］ GALLEGO N C，EDIE D D， NYSTEN B，et al.The thermal conductivity of ribbon⁃shaped carbon fibers［J］.Carbon，2000，38（7）：1003－1010.

［2］ LU S L，RAND B.Large diameter carbon filaments from mesophase pitch for thermal management applications［J］.New Carbon Materials，2000，15（1）：1－5.

［3］ MANOCHA L M，WARRIER A，MANOCHA S，et al.Thermophysical properties of densified pitch based carbon／carbon materials—I.Unidirectional composites［ J］.Carbon， 2006， 44（3）：488－495.

［4］冯志海，樊桢，孔清，等.高导热碳／碳复合材料的制备［J］.上海大学学报（自然科学版），2014（1）：51－58.

［5］ PIRAUX L，ISSI J P，COOPMANS P.Apparatus for thermal conductivity measurements on thin fibres［J］.Measure⁃ment，1987，5（1）：2－5.

［6］ MAY P W，PORTMAN R，ROSSER K N.Thermal con⁃ductivity of CVD diamond fibres and diamond fibre⁃reinforced ep⁃oxy composites［J］.Diamond ＆ Related Materials，2005，14（3）：598－603.

［7］ ZHANG X，FUJIWARA S，FUJII M.Measurements of thermal conductivity and electrical conductivity of a single carbon fiber［J］.International Journal of Thermophysics，2000，21（4）：965－980.

［8］ WANG J L，MING G U，WEIGANG M A，et al.Temper⁃ature dependence of the thermal conductivity of individual pitch⁃derived carbon fibers［J］.New Carbon Materials，2008，23（3）：259－263.

［9］王建立，顾明，马维刚，等.用变长度“T”形法测量单根纤维热导率［J］.工程热物理学报，2009，30（12）：2068－2070.

［10］王照亮，唐大伟，郑兴华，等.3ω法测量单根碳纤维导热系数和热容［J］.工程热物理学报，2007，28（3）：490－492.

［11］ YAMANE T，KATAYAMA S，TODOKI M，et al.Ther⁃mal diffusivity measurement of single fibers by an ac calorimetric method［J］.Journal of Applied Physics，1996，80（8）：4358－4365.

［12］ LU S，BLANCO C，RAND B.Large diameter carbon fi⁃bres from mesophase pitch［J］.Carbon，2002，40（12）：2109－2116.

［13］马兆昆，刘朗，刘杰.纺丝工艺对带形中间相沥青基石墨纤维取向结构及热导率的影响［J］.无机材料学报，2010，25（9）：989－993.

［14］张万军，张福全，黄娅妮.电路板式四点法测定沥青碳纤维单丝轴向电阻率［J］.炭素，2012（3）：8－12.

［15］ 贺福，杨永岗.超级导热型沥青基碳纤维［J］.高科技纤维与应用，2003，28（5）：27－31.

［16］ HIROSHI H，TETSUO B，MASUMI H.Pitch⁃based carbon fiber web：EP，EP2180094 A1［P］.2010.

［17］ HIROSHI H，MASUMI H，TETSUO B.Carbon fiber composite sheet，use thereof as a heat conductor and pitch⁃based carbon fiber web sheet for use in the same：US，US20090061193［P］.2009.

［18］ MASUMI H，HIROSHI H，TETSUO B.Pitch⁃based carbon fiber，web and resin molded product containg them：US，US20100068496［P］.2010.

［19］ YAMAMOTO I，YOSHITANI A，NAKAKOSHI A.Woven fabric of carbon fiber：JP，JP1998－194117［P］.1998.

［20］ LAVIN J G，BOYINGTON D R，LAHIJANI J，et al.The correlation of thermal conductivity with electrical resistivity in mcsophase pitch⁃based carbon fiber［J］.Carbon，1993，31（6）：1001－1002.

［21］袁观明.高导热炭材料的制备研究［D］.武汉科技大学，2012.

［22］ MINUS M，KUMAR S.The processing， properties，and structure of carbon fibers［J］.JOM，2005，57（2）：52－58.

［23］赵稼祥.日本三菱化学公司沥青基碳纤维的进展——国外碳纤维进展之六［J］.高科技纤维与应用，2001，26（3）：10－14.