两种典型缺陷对六边形蜂窝压缩性能的影响

卢子兴 黄纪翔

（北京航空航天大学固体力学研究所，北京 100083）

0 引言

蜂窝因在压缩变形下表现出优异的能量吸收特性，且具有良好的多功能性和较强的可设计性，故引起国内外学者们的广泛关注。对规则蜂窝而言，可在单胞基础上建立细观力学模型来预测其宏观性能［1］。然而，蜂窝制备过程中存在缺陷是不可避免的，所以研究缺陷对蜂窝力学行为的影响很有必要。SILVA等［2］讨论了随机移除壁面这种缺陷形式对周期性蜂窝以及随机Voronoi蜂窝力学性能的影响；GUO等［3］也分析了胞元缺失对规则六边形蜂窝弹性模量和后屈曲行为的影响；CHEN等［4］研究了6种缺陷对二维蜂窝面内屈服性能的影响；LI等［5］讨论了胞体的形状不规则性及壁厚不均匀分布对蜂窝弹性模量的影响；WANG等［6］考虑了缺陷率对不同形状蜂窝体的敏感性，分析了四边形和三角形金属蜂窝中胞壁缺失对蜂窝面内有效弹性模量和初始屈服应力的影响；AJDARI等［7］基于规则的六边形模型和随机模型，分析了集中孔洞和部分填充孔对蜂窝弹塑性行为的影响，发现缺陷的位置对其弹性行为影响不大。

本文利用数值模拟研究了孔洞和部分填充孔穴这两种典型的缺陷对弹性蜂窝（橡胶）和弹塑性蜂窝（金属）的压缩性能的影响规律。

1 模型的建立

规则完整的正六边形蜂窝结构是到目前为止最常见的一种蜂窝结构。其面内刚度和强度最低，因在该平面内的应力会使孔壁产生弯曲变形，而其面外刚度和强度则要大得多。本文采用商业有限元软件ANSYS@（ANSYS Inc.， Canonsburg，PA）进行分析，并选用BEAM23梁单元来模拟孔壁材料，用数值模拟方法研究蜂窝在面内方向的弹性屈曲和塑性坍塌行为。选用模型尺度为20个单胞×20个单胞，相对密度为0.1的蜂窝结构进行研究。

当基体材料为铝时，采用理想弹塑性模型，且取弹性模量 E＝70 GPa，屈服强度 σy＝130 MPa，泊松比ν＝0.3；为了便于对比分析，纯弹性蜂窝的基体弹性性能参数也设为 E＝70 GPa，ν＝0.3；另外，为了研究蜂窝的孔壁屈曲和材料屈服之间的耦合作用，进一步比较了屈服强度σy＝1.4 GPa，即屈服应变为2%的结果。

首先利用非线性屈曲分析来得到完整的蜂窝结构的应力－应变响应曲线，然后引入两类典型的缺陷：部分填充孔穴以及集中或分散孔洞，其模型示意图分别如图1所示。在非线性屈曲分析中，首先进行特征值屈曲分析，然后根据其屈曲模态施加一定比例的初始扰动进行分析计算。这里主要研究沿着面内方向加载的情况，在上表面施加一个位移，下表面约束沿面内方向的位移，放松其他方向的自由度，而两个侧面是自由的。

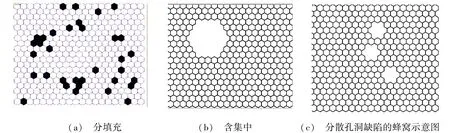
图1 含孔穴缺陷的蜂窝示意图Fig.1 Diagram of honeycombs with defects filled cells，concentrated and scattered holes

2 结果与讨论

2.1 完整蜂窝材料的模拟结果

Gibson和Ashby［3］基于正六边形蜂窝的微结构给出了理论预测其弹性模量、弹性屈曲应力及塑性坍塌应力的公式，据此可以估算其对应的弹性屈曲应变及塑性坍塌应变，还可以得到弹性屈曲和塑性坍塌应力相等时基体材料的临界参数。为了便于比较，本文研究了屈服应变为2%（σy＝1.4 GPa）的弹塑性基体制成的蜂窝，通过与常见铝（σy＝130 MPa）蜂窝的性能进行对比来分析其塑性坍塌与孔壁稳定性之间的关系。 计算得到σy＝130 MPa和σy＝1.4 GPa的基体分别对应的塑性坍塌应力为0.65和7.0 MPa。

图2给出了由三种不同基体制成的完整蜂窝结构的压缩应力－应变曲线。

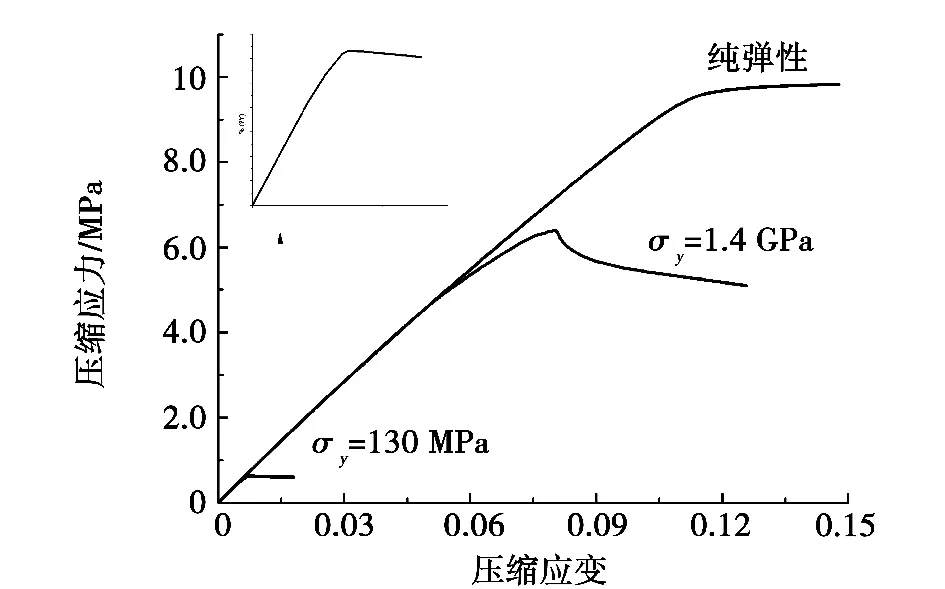
对于纯弹性基体，本文算得的结果和理论值吻合得较好，从图中可以看出大约在应变为0.1时结构整体发生屈曲；当进入后屈曲变形阶段之后，结构会达到新的平衡，仍具有一定的残余刚度，应力－应变曲线还会继续缓慢地上升。对于基体σy＝1.4 GPa的蜂窝，结构的弹性屈曲应力比较接近其塑性坍塌应力。有限元模拟得到的塑性坍塌应力为6.37 MPa，其相比理论估算值7.0 MPa低了9%左右。由于蜂窝结构的主要变形机制是倾斜孔壁的弯曲变形，因此最大应力总是发生在倾斜孔壁的结点处。当其结点处开始进入屈服后，根据塑性滑移理论，在最大剪应力方向会产生塑性流动，导致结构中部分竖直的孔壁有偏转趋势，从而使结构内部产生新的不均匀的应力分配。最终的结果是其中一部分倾斜孔壁的结点先进入屈服，而不是所有倾斜孔壁的结点同时达到屈服强度，这在应力－应变曲线上对应的就是非线性上升阶段。随着应力的增加，当部分孔壁内的局部应力达到其弹性屈曲应力时，结构内将开始形成局部变形带，这时蜂窝结构达到其最大塑性坍塌应力点。由于基体屈服强度为1.4 GPa的蜂窝结构的塑性坍塌应力比较接近弹性屈曲应力，故其孔壁屈服与屈曲将会强烈地耦合在一起从而导致局部失稳现象加剧，使结构承载能力大大减弱，因此应力－应变曲线在过了最大点后迅速下降。图3给出了在蜂窝结构最大切应力方向上形成的局部变形带，该局部变形带的形成，会使应力逐渐稳定在一个平台区域，由于这里面涉及到孔壁的接触等复杂问题，暂不考虑形成局部变形坍塌带之后的应力－应变曲线。

图3 弹塑性蜂窝中形成的局部变形带示意图Fig.3 Local deformation band diagram in elasto⁃plastic honeycombs

对于基体σy＝130 MPa的蜂窝，计算得到的曲线见图2中的小图，在最大应力为0.63 MPa处达到屈服，比估算值0.65 MPa低了约3%。图4为塑性坍塌时蜂窝孔壁的应力云图，可以看出，应力主要集中在倾斜的孔壁上，并且在两端结点处最先达到其屈服强度，从而使蜂窝结构整体塑性坍塌；而竖直的孔壁中的应力较小，小于其弹性屈曲应力，故未发生弹性屈曲。与基体σy＝1.4 GPa的蜂窝材料不同的是，此时结构的弹性屈曲应力远大于其塑性坍塌应力，所以结构发生塑性坍塌以后不会引起屈曲失稳现象，而是孔壁绕着端点处形成的塑性铰发生旋转。由于孔壁的塑性矩是定常值，而孔壁发生旋转会致使力矩略有增大，因此其应力会略有下降。

图4 弹塑性蜂窝达到塑性坍塌强度时的应力云图（σy＝130 MPa）Fig.4 Stress nephogram of elasto⁃plastic honeycombs when reached the plastic collapsed strength

2.2 含集中孔洞缺陷的蜂窝材料的模拟结果

考虑了5%，10%，15%三种孔洞缺陷的模拟结果，图5为含15%集中孔洞的蜂窝结构的一阶屈曲模态图，可以看出由于孔洞的存在破坏了结构的完整性，其附近会应力集中，从而会影响蜂窝材料的变形机制。

图5 含15%集中孔洞的蜂窝一阶屈曲模态图Fig.5 First buckling mode diagram of honeycombs

图6 为含有集中孔洞的纯弹性蜂窝材料的压缩应力－应变曲线。从图中可以看出，随着孔洞所占比例的增大，蜂窝的弹性模量和弹性屈曲应力都逐渐下降，15%的孔洞使弹性模量下降了20%，而弹性屈曲应力则下降了33%左右。由于缺陷的存在，使蜂窝在孔洞附近提前发生局部屈曲，进而形成局部变形带，所以应力－应变曲线中没有完整结构的整体屈曲后继续上升的趋势。相反，局部变形带的产生会使应力有所下降，最终其稳定在一个平台区域。

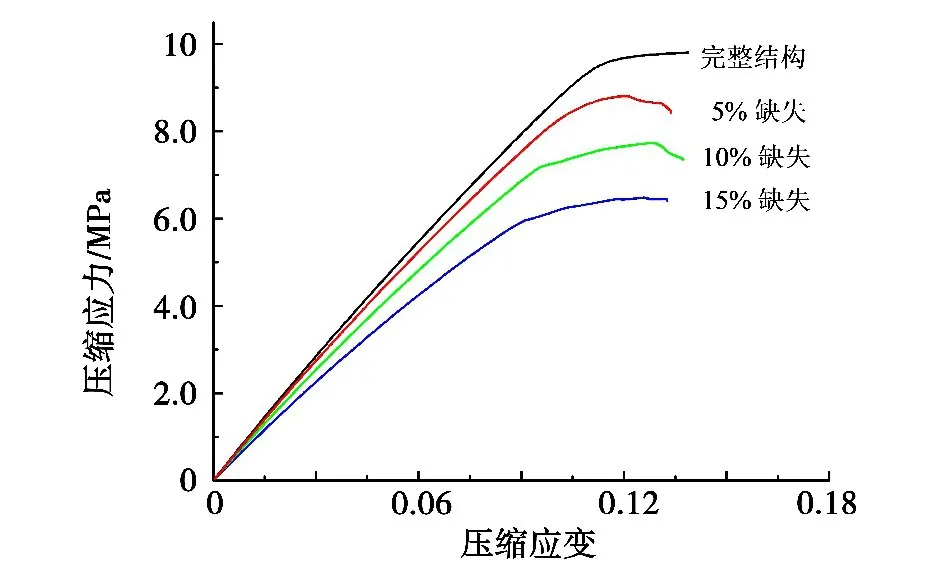
图6 含集中孔洞的纯弹性蜂窝的压缩应力－应变曲线Fig.6 Compressive stress⁃strain curves of elastic honeycombs with concentrated holes

图7 为含集中孔洞的弹塑性蜂窝材料的压缩应力－应变曲线。从图7（a）中可以看出，集中孔洞使其弹性模量和塑性坍塌应力下降较大，15%的孔洞使其弹性模量下降了21.4%，而塑性坍塌应力则下降了33.7%，相同比例的孔洞缺陷对弹性屈曲／塑性坍塌应力的影响比对弹性模量的影响要大。与纯弹性蜂窝不同的是，孔洞的存在虽然使结构整体的承载能力下降，但是并没有改变其主要的变形机制。随着孔洞所占比例的增加，结构的完整性被严重破坏，孔洞附近应力集中效果明显，故其附近孔壁会较早地进入屈服并进一步诱导竖直的孔壁发生屈曲，开始形成一个沿水平方向的局部变形带，并导致应力－应变曲线在过了最大应力后下降的趋势有所缓和。从图7（b）看到，集中孔洞使其弹性模量、塑性坍塌应力及应变都大幅下降，15%的孔洞使其弹性模量下降了22.8%，而塑性坍塌应力则下降了34.0%。由此可见，对不同的基体组成的蜂窝材料，相同比例的孔洞对其力学性能的削弱作用相同。

图7 含集中孔洞的弹塑性蜂窝的压缩应力－应变曲线Fig.7 Compressive stress⁃strain curves of elasto⁃plastic honeycombs with concentrated holes

2.3 含分散孔洞缺陷的蜂窝材料的模拟结果

图8 为含15%分散孔洞的蜂窝结构的一阶屈曲模态图。可以看出，在离边界距离最近的孔洞附近应力集中效果最明显，最先出现孔壁屈曲；其他孔洞附近的应力集中效果则被弱化了。与集中分布的孔洞相比，分散孔洞对整个结构完整性的破坏要小一些，故其对蜂窝结构力学性能的影响也要小一些。

图8 含15%分散孔洞蜂窝的一阶屈曲模态图Fig.8 First buckling mode diagram of honeycombs with 15%scattered holes

可以看出，集中孔洞对弹性模量的降低更显著，其线弹性阶段的长度也明显减少；并且15%的集中孔洞能使弹性屈曲应力下降33%，而15%的分散孔洞使弹性屈曲应力只下降了20%左右。图10为含有集中和分散孔洞的弹塑性蜂窝材料的压缩应力－应变曲线。对于基体σy＝130 MPa的蜂窝，15%的集中孔使塑性坍塌应力下降33.7%，而15%的分散孔则只下降21%；而对于基体 σy＝1.4 GPa的蜂窝，集中和分散孔洞得出的结果之间的差异就变得比较小了。

图9为含有集中孔洞和分散孔洞的纯弹性蜂窝材料的压缩应力－应变曲线。

图10 含集中和分散孔洞的弹塑性蜂窝的压缩应力－应变曲线Fig.10 Compressive stress⁃strain curves of elasto⁃plastic honeycombs with scattered and concentrated holes

图9 含集中和分散孔洞纯弹性蜂窝的压缩应力－应变曲线Fig.9 Compressive stress⁃strain curves of elastic honeycombs with concentrated and scattered holes

2.4 含部分填充孔穴的蜂窝材料的模拟结果

选用板单元plane42来模拟填充孔穴，填充的孔穴起到了增强结构承载能力的作用，由于在填充孔穴附近容易发生应力集中，结构的屈曲模式也由整体屈曲变为局部屈曲失稳。图11为含5%填充孔穴的蜂窝材料的一阶屈曲模态图，由于填充孔穴的引入，结构在承载能力最弱的那一层会最先发生屈曲变形。

图11 含5%填充孔穴的蜂窝材料的一阶屈曲模态图Fig.11 First buckling mode diagram of honeycombs with 5%filled cells

图12 为不同填充比例的纯弹性蜂窝材料的压缩应力－应变曲线。可以看出，随着填充比例的增加，弹性模量急剧地增大，并且最大屈曲应力也在增大。填充孔穴的引入，使得不再出现整体屈曲失稳的情况，而是使局部区域内的孔壁先发生失稳。填充5%孔穴的蜂窝结构的应力－应变曲线在屈曲后不再上升，而是稳定在一个平台区域，从图12右图的变形示意图中可以看出蜂窝中已经开始出现局部失稳变形带。而当填充孔穴20%时，结构已经很难再形成这种失稳变形带了，故其应力－应变曲线中没有平台区域，如图12中最上面的曲线所示。图13为不同填充比例的弹塑性蜂窝材料的压缩应力－应变曲线。可以看到，填充孔穴的引入使弹塑性蜂窝材料的刚度得到较大的提高；同时，填充也引起了局部的应力集中，从而使蜂窝提前进入塑性区。因此，填充比例越大，其应力－应变曲线中线弹性段越短，弹性极限也越低，相应地弹性极限到塑性屈服点之间的曲线弧度明显加大。

图12 不同填充比例的纯弹性蜂窝材料的压缩应力－应变曲线Fig.12 Compressive stress⁃strain curves of elastic honeycombs with different fractions of filled cells

图13 不同填充比例的弹塑性蜂窝材料的压缩应力－应变曲线Fig.13 Compressive stress⁃strain curves of elasto⁃plastic honeycombs with different fractions of filled cells

另外，从两幅图中完全不同的应力响应结果可以看出基体材料的屈服强度直接决定了填充后的蜂窝材料的力学性能。对于基体σy＝130 MPa的蜂窝，填充后其弹性模量增大的非常快，但是其塑性坍塌应力基本保持不变。这是由于结构的屈服强度相比其屈曲应力要低很多，因此当局部有孔壁发生屈服后，不会诱导结构的局部屈曲失稳，所以结构可以保持在一个稳定的塑性坍塌平台区。对于蜂窝材料，当整体结构或其中某一层结构失去承载能力时，其应力－应变曲线会进入平台区：对完整的蜂窝材料，其平台区代表的是结构的整体失效（所有的倾斜孔壁端部都形成塑性铰）；对填充比不大的蜂窝材料，由于填充孔穴在每一层的分布是随机不均匀的，其平台区代表结构最弱的那一层达到失效（该层的倾斜孔壁端部都形成塑性铰）。在这两种失效形式下得到的结构的静平衡力非常接近，所以基体屈服应力为130 MPa的蜂窝，在填充比例较小时，其平台区应力几乎没有降低。这里需要指出的是，当填充比例较大时，结构的失效将表现出很强的局部性，不再是某一层结构失效，而是以未填充的孔穴为中心的局部区域发生失效。考虑到在实际蜂窝材料的生产加工中引入的填充孔穴比例较少，所以本文主要在较低的填充比下研究填充孔穴对蜂窝材料的弹塑性力学性能的影响，此时失效形式仍然为结构最弱层先失效。对于基体σy＝1.4 GPa的蜂窝，结构进入塑性失效后，其压缩应力－应变曲线并没有相对稳定的平台，而是急剧的下降，这一点在对完整蜂窝材料的分析中已详细解释。填充孔穴的引入使其塑性坍塌应力降低了8%左右，而填充比例的不同却对该塑性坍塌应力影响不大。这是由于此时结构的屈曲应力比较接近其塑性坍塌应力，而填充所导致的局部应力集中使部分竖直孔壁先发生了屈曲，相当于降低了结构的承载能力，所以此时的塑性坍塌应力比完整的情况小。同样地，当填充比例较小时，不同填充比的蜂窝虽然整体结构变形完全不同，但最弱层的结构变形却基本相似（发生屈曲的竖直孔壁比例相当），所以得到的塑性坍塌应力也非常接近。与孔洞缺陷的影响所不同的是，填充孔穴对弹性模量的影响要远大于其对屈曲／坍塌应力的影响；对不同基体的蜂窝材料的弹性屈曲／塑性坍塌应力，填充孔穴起到完全不同的效果。

3 结论

研究了两种典型缺陷，即孔洞和填充孔穴对蜂窝材料纯弹性及弹塑性力学行为的影响。对于含孔洞缺陷的蜂窝材料，比较了集中孔洞和分散孔洞对其应力－应变行为的影响，结果发现，集中孔洞对其力学行为影响更大，且它们的存在完全改变了材料的变形模式；对于含填充孔穴的蜂窝材料，其弹性模量得到显著增强，纯弹性蜂窝材料的屈曲应力也得到增强，但弹塑性蜂窝的塑性坍塌应力则保持不变或有所下降。

［1］ GIBSON L J，ASHBY M F.Cellular Solids：Structure and Properties［M］.Seconded.Cambridge University Press，Cam⁃bridge，1997.

［2］ SILVA M J，GIBSON L J.The effect s of non⁃periodic microstructure and defects on the compressive strength of the two dimensional cellular solids［J］.International Journal of Mechanical Sciences，1997，39（5）：549－563.

［3］ GUO X E，GIBSON L J.Behavior of intact and damaged honeycombs：A finite element study［J］.International Journal of Mechanical Sciences，1999，41（1）：85－105.

［4］ CHEN C，LU T J，FLECK N A.Effect of imperfections on the yielding of two dimensional foams［J］.Journal of the Me⁃chanics and Physics of Solids， 1999，47（11）：2235－2272.

［5］ LI K，GAO X L，SUBHASH G.Effect s of cell shape and cell wall thickness variations on the elastic properties of two⁃dimensional cellular solids［J］.International Journal of Solids and Structure，2005，42（526）：1777－1795.

［6］ WANG A J，MCDOWELL D L.Effects of defects on in⁃plane properties of periodic metal honeycombs［J］.International Journal of Mechanical Sciences，2003，45（11）：1799－1813.

［7］ AJDARI A，NAYEB⁃HASHEMI H，CANAVAN P，et al.Effect of defects on elastic⁃plastic behavior of cellular materials［J］.Materials Science and Engineering A，2008，487：558－567.