空位缺陷对单层石墨烯导热特性影响的分子动力学

熊良涛，王继芬，谢华清，章学来

（1上海海事大学商船学院，上海 201306；2上海第二工业大学资源与环境工程学院，上海 201209）

随着科学技术的快速发展，电子元件的尺寸越做越小，其处理数据能力要求却越来越高。微纳米尺寸的电子元件在处理数据时是一个高产热过程，需要对元件进行快速散热降温以保证其工作性能及稳定性，因此超薄高导热的材料成为了电子元件发展至关重要的一环。单层石墨烯(single-layer graphene，SLG)的高导热性使其成为最为理想的二维导热材料。它最早是由Novoselov等[1]在2004年通过微机械剥离获得，使得其在微纳米尺度传热领域的应用成为了可能。SLG优异的物理化学性质引起广大研究者的研究兴趣，它相比于传统的硅基材料表现出更加出色的力学性能[2]、磁化性能[3]和光学性能[4]，也是厚度最薄、强度最硬的纳米材料。通过机械剥离的方法得到的SLG 在室温下导热率高达3080～5150 W/(m·K)[5]，同时其在传热[6]、光电[7]、传感器[8]及能量存储领域[9]都显示出巨大的应用潜力。

在材料的制备过程中，完美的SLG 晶格结构很难存在，晶体内部往往包含着大量缺陷，常见的缺陷包括了单空位(single-vacancy，SV)、双空位(double-vacancy，DV)和stone-wales(SW)缺陷等[10]。人们发现缺陷的存在会给SLG的特性带来一定的影响。首先，缺陷能够影响SLG的机械强度，通过调控缺陷来获得SLG 某些性能的同时伴随着机械强度下降[11]。Wang 等[12]通过第一性原理密度泛函理论来研究SLG 的光热性质，发现缺陷SLG引起了红外光谱和拉曼光谱的波峰和分裂。关于SLG 的热导率，Liu 等[13]深入研究了缺陷及其位置对于SLG 热导率的影响，发现缺陷对于SLG 热导率影响非常显著。Yang 等[14]研究了掺杂的氮原子与SW缺陷之间距离远近对SLG热导率的影响，且通过氮原子对缺陷SLG进行改性。Sun等[15]通过分子动力学模拟研究发现含有SV 或DV 缺陷的SLG聚合物纳米复合材料拉伸后材料的总体性能，包括杨氏模量、极限强度和两个方向的应变都随着缺失原子数量的增加而降低，但对缺陷分布不敏感。目前对于含有SV和DV缺陷的SLG热导率研究较少，以及SLG 热导率在尺寸、温度和缺陷浓度等因素影响下的研究不够全面。

在本文中，采用非平衡分子动力学(NEMD)的方法研究了SLG的尺寸效应，以及温度和缺陷浓度等因素对SLG热导率的影响，重点分析了受SV与DV缺陷调制的SLG的热导率之间的差异。该研究将对不同温度下及不同空位缺陷类型和缺陷浓度SLG的热导率的研究与应用提供一定理论参考，同时为微纳米传热中SLG的应用提供一定的理论指导。

1 模型与方法

1.1 计算模型

采用LAMMPS 软件包[16]对扶手椅形(x方向)SLG 纳米带热输运特性进行NEMD 模拟研究。同时采用了Broido和Lindsay[17]的Tersoff势描述C—C原子间相互作用。为避免周期性图像之间的相互作用，在模拟过程中对所有x、y、z方向[18]都施加了周期边界条件，并在厚度z方向设置了厚度为20 nm的真空层。如图1所示为完美、SV和DV缺陷的SLG 二维原子构型，由于独特的原子构型，SLG分为两种手性，即扶手椅形和之字形(y方向)。两种手性的SLG 热导率之间存在着一定的差异[19]，为减少边界条件对热导率研究的影响及增加研究结果的可靠性，同时考虑到边界条件的一致性，本文单一围绕扶手椅形SLG 进行研究。本文研究了SV、DV两种缺陷类型对SLG热导率的影响。通过从石墨烯体系中分别去除1个碳原子和2个相邻的碳原子，引入了SV缺陷和DV缺陷，建立如图1所示的SV 缺陷SLG(SVSLG)与DV 缺陷SLG(DVSLG)两种缺陷物理模型。在本文中的缺陷都是随机且均匀分布在模型的内部[20]。

图1 完美、SV和DV缺陷SLG的结构Fig.1 Schematic diagram of perfect,SV and DV defect structures of SLG

1.2 NEMD模拟

在SLG 热导率的NEMD 模拟中，原子运动方程积分步长设置为0.5 fs。模拟开始时，先将系统结构松弛使系统模型能量最小化以达到稳定状态。紧接着将系统置于0 bar 的等温-等压系综(NPT)中500 ps，然后再进入300 K 的正则系综(NVT)500 ps。经过前两个周期共计1 ns 的模拟时间后，系统结构松弛至平衡态，如图2所示。图中SLG系统结构中的原子保持在系统的边界框内，未出现原子外溢现象。最后，将该系统放入额外500 ps 的微正则系综(NVE)中直至平衡。

图2 1 ns模拟时间后SLG系统的结构Fig.2 Structure of SLG system after 1 ns simulation time

图3(a)给出NEMD 模拟SLG 模型用于计算其面内热导率。模型的长度L定义为图中热源中心到热汇中心距离的两倍。在模拟过程中，热源(红色区域)位于x=1/4L的中心位置，同时在对应模型x=3/4L的位置设置一个面积相同的热汇(蓝色区域)。系统达到平衡态之后，分别对热源和热汇区域施加朗之万局部热浴，热源和热汇的温度分别保持在320 K和280 K[21]。经过5 ns 热浴模型内部温度分布达到稳定。系统内原子某一刻的温度计算公式如下

式中，T为原子温度；m为原子的质量；Vi为第i个原子速度；Nl为原子总数；kB为波尔兹曼常数。将模型沿着长度方向等分为100块，统计每块模型内原子的平均温度，最终得到300 K下模型长度方向的温度分布如图3(a)所示。从图中发现热源和热汇周围出现了较大的温度落差，由于SLG 的尺寸远小于其自身有效声子平均自由程(effective mean free path，EMFP)775 nm[5]，热源和热汇附近会产生声子散射，最后出现温度跳跃的现象。

图3 SLG模型中的温度分布与能量变化Fig.3 Temperature distribution and energy variation in SLG model

图3(b)显示了热源的输出能量和热汇的输入能量。通过图3(b)的线性拟合得到两个热通量，热通量的绝对值取平均得到体系的热流速率。最后利用傅里叶导热定律计算稳定系统的热导率k

式中，Q为热流速率；A为横截面积；∂T/∂x为温度梯度；k为面内热导率。由于周期性边界条件，在式(2)中增加了一个常数2。能量从热源向热汇方向流动截面积为

式中，δ为模型的厚度；W为模型的宽度。在本文研究中，SLG的宽度δ固定为0.33 nm。

2 结果与讨论

2.1 尺寸效应

2.1.1 宽度对SLG热导率的影响

模拟300 K 下相同长度下SLG 的热导率与其宽度之间的关系，选取的SLG 长度(L)为20.5 和100.9 nm，宽度(W)分别为3.5、6.4、10.4、15.3和20.2 nm，计算结果如图4所示。由图4得到：L为20.55 nm、100.9 nm 的SLG 的热导率都随着宽度增加而逐渐的增大，同文献报道趋势一致[22]。在宽度相同条件下L为100.9 nm 的SLG 热导率远大于L为20.5 nm的SLG热导率。SLG的热导率随着宽度增加而增大的主要原因：宽度较小时，截面面积小不利于声子的运输，边界散射作用强，声子运动遭到限制；截面面积越大，导致边界散射作用被减弱，声子在面内运动更加方便快捷，从而使热导率随着宽度的增加不断增大。

图4 宽度对300 K时SLG体系热导率的影响Fig.4 Effect of width on thermal conductivity of SLG system at 300 K

2.1.2 长度对SLG热导率的影响

图5 所示为300 K 下长度对SLG 热导率的影响。其中，W固定为3.5和10.4 nm，分别计算了L为5.1、20.5、50.4、80.3、100.9 和150.4 nm 的SLG 的热导率。由图5 可见，W分别为3.5 和10.4 nm的两条SLG热导率曲线具有相同的变化趋势并且两条曲线之间差值很小。图中SLG 的热导率都是随着长度的增加而不断增大，与文献值变化趋势一致[23]。本文涉及SLG 的最大尺寸150 nm，远小于已知SLG的EMFP(775 nm)，因而会出现卡西米尔效应[24]，导致SLG热导率计算数值比无限长的SLG 热导率值要小。模型尺寸较小(<775 nm)时，其内部的声子以弹道的方式进行热输运，尺寸效应使得SLG 热导率随着模拟长度的增加不断增大。同时由于宽度相比长度对SLG 热导率的影响较小，导致图4 中两条热导率曲线之间的差值很小。

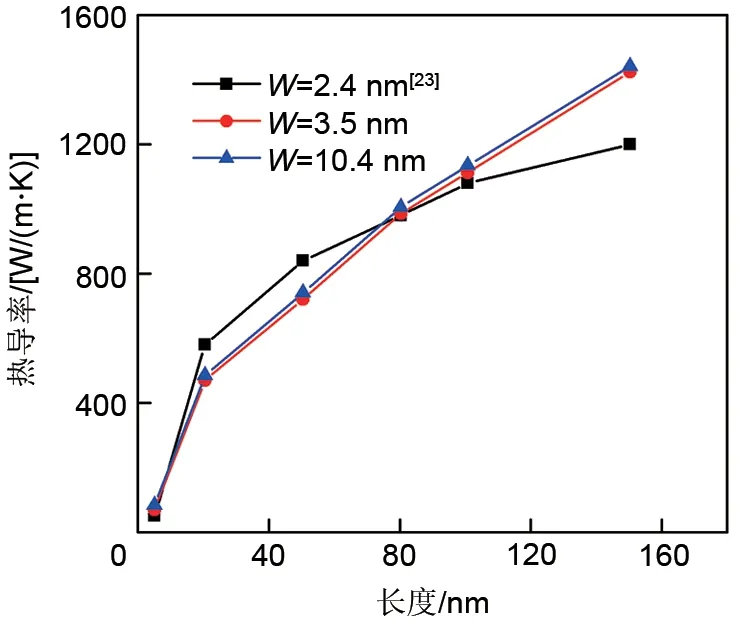
图5 长度对300 K时SLG体系热导率的影响Fig.5 Effect of length on thermal conductivity of SLG system at 300 K

2.1.3 拟合无限长SLG热导率

在NEMD 模拟过程中SLG 模型的尺寸越大，计算所耗费的机时越长。当模拟尺寸不断放大达到几百纳米，耗费的机时呈几何倍数增长。为了尽可能地节约机时同时得到无限长SLG 的热导率，本文先计算多个小尺寸模型的热导率，再使用以下公式拟合得到无限长度SLG模型的热导率[24]

式中，l为有效声子平均自由程；k∞为模型长度为无穷大(L→∞)时的SLG热导率(固有热导率)。

图6拟合了长度倒数与热导率倒数之间线性关系，并且计算得到了温度300 K，W为3.5和10.5 nm时SLG的k∞热导率。图6中包含了两条在不同宽度条件下的热导率拟合曲线，得到的拟合曲线均为直线，符合式(4)中的线性关系，且SLG 的热导率点都均匀分布在两条拟合曲线上。图6中两条SLG的热导率拟合直线在x轴上的截距表示为：SLG在W为3.5 和10.5 nm 时的k∞热导率分别为2637.9 和2667.6 W/(m·K)，两个k∞热导率之间的差值不大，数值大小都是处于2000～3000 W/(m·K)之间，与文献值接近[25]。

图6 SLG沿扶手椅方向的长度倒数与导热率倒数之间的关系Fig.6 Relationship between inverse lengths and inverse thermal conductivities of SLG along armchair direction

2.2 缺陷浓度对SLG热导率的影响

模拟300 K 下缺陷对固定尺寸W为6.41 nm、L为20.51 nm SLG 热导率的影响，分别计算缺陷浓度0%(perfect，完美)-0.5%下，受SV 和DV 缺陷调制的SLG 的热导率并将计算的结果归一化处理为相对热导率，计算结果如图7所示。其中缺陷浓度为缺陷原子总数除以完美SLG 的原子总数；SLG热导率的归一化表示为300 K时某缺陷浓度下SLG的热导率与完美SLG的热导率的比值。图7主要由SVSLG与DVSLG的两条热导率曲线构成，两条曲线的变化趋势都是随着缺陷浓度的增加不断下降，但DVSLG的热导率曲线位于SVSLG的热导率曲线上方。具体数据变化如下：完美SLG在300 K时的热导率为477.9 W/(m·K)，当该模型中DV缺陷浓度为0.5%时，DVSLG 的热导率减小到132.2 W/(m·K)；然而当SV缺陷浓度为0.5%时，SVSLG的热导率减小到166.5 W/(m·K)，小于0.5%DVSLG的热导率；并且缺陷浓度一定，温度300 K 时，DVSLG 的热导率都较大于SVSLG 的热导率。从图7 的插图中可见，SVSLG 与DVSLG 的两条相对热导率(k/k0)曲线都是不断下降的变化趋势，且曲线上点的数值都小于等于1，其中k0为完美SLG在300 K时的热导率。相同缺陷比下，DVSLG 曲线上相对热导率值大于SVSLG 曲线上的相对热导率值。其中0.5%DVSLG 的相对热导率为27.7%，较大于相同缺陷浓度下SVSLG 的相对热导率24.4%。结果表明随着缺陷浓度的增加，DVSLG 的热导率减少量小于SVSLG 的热导率减小量。文献[21]中类似的研究也发现相对热导率随着缺陷浓度的增大不断减小的规律，且温度300 K下0.5%SV缺陷下SLG的相对热导率为30%，接近于本文的24.4%，验证了本文研究的可靠性。同时由于一些参数设置的不同，不可避免地导致研究结果存在着一定的差异性。

图7 缺陷浓度对SV和DVSLG模型热导率的影响Fig.7 Effects of defect concentration on thermal conductivity of SV and DVSLG models

根据经典晶格导热理论，SLG热导率与声子平均自由程成正比。SLG热导率也可表示为

式中，c为SLG 的比热容；v为声波在SLG 中的声子群速度；λ为声子的EMFP。SLG 的EMFP是由声子-声子散射决定的。然而，由于系统中存在缺陷，λ被修正为：

式中，lp-p为声子-声子散射长度；ld-p为缺陷引起的散射长度。

固体材料的热传导方式主要为两种，分别为声子传热和电子传热，SLG材料的热传导方式主要是声子传热。材料内部声子热输运机理[26]表明，缺陷浓度小于0.5%时，缺陷对于SLG的比热容和声子群速度的影响较小，对声子平均自由程的影响较大。由于缺陷为原子的缺失，声子传热时在缺陷的位置会发生声子局部散射，进而产生局部的热阻。缺陷的浓度越大发生局部散射的声子越多，进而局部热阻越大，最终导致SLG的热导率下降。同时，由于缺陷引发SLG 内部声子散射，伴随等式(6)中的ld-p项的增加，λ项的降低，最终导致SLG热导率减小。

由图7还可看出SLG的两条热导率曲线都是急剧下降的趋势，当缺陷浓度达到0.2%时，SLG的两条热导率曲线的下降趋势明显变缓。当缺陷浓度从0%增加到0.2%时，相比完美SLG在300 K时的热导率477.9 W/(m·K)，受SV和DV缺陷调制的SLG的热导率下降明显，分别降低到200.8 W/(m·K)和222.0 W/(m·K)。0.2%SVSLG与0.2%DVSLG的相对热导率较完美SLG减少了58.0%和53.6%。缺陷浓度从0.2%增加到0.5%时，SVSLG与DVSLG的热导率分别减少了84.3 W/(m·K)和89.9 W/(m·K)，热导率减小量远小于缺陷浓度从0%到0.2%时两个系统模型热导率的减少量。与SVSLG 的热导率曲线相比，DVSLG曲线变化更稳定，DVSLG的热导率随缺陷浓度的变化更小。热导率曲线先快速下降后平缓的主要原因是随着缺陷浓度的增加，系统的热传递经历了由传播机制向扩散机制的转变，声子输运过程变得无序[27]。SLG 中的缺陷浓度越大，声子的扩散越来越小，最终SLG 热导率曲线下降幅度变得平缓。在缺陷浓度相同时，DV缺陷与SV缺陷的总缺失原子数目必然相同。然而，在每个SLG缺陷中心，SV缺陷中缺失一个C原子，DV缺陷中缺失两个C 原子，最终得到SVSLG 的缺陷中心是DVSLG 的2 倍。解释了SVSLG 缺陷系统比DVSLG缺陷系统包含更多的缺陷散射，SVSLG热导率下降得更明显。

声子态密度(PDOS)是表征二维材料中声子活动的一种单一而有力的方法。PDOS是通过计算平衡模式下原子速度自相关函数的傅里叶变换得到的[28]

为了从内部微观声子运动来分析热导率的变化，模拟了缺陷对固定尺寸W为6.41 nm，L为20.51 nm的SLG声子频率分布的影响，计算得到了具有不同缺陷浓度的SLG模型的PDOS图。图8为受SV和DV缺陷调制的SLG在缺陷浓度为0%(perfect)、0.1%、0.3%和0.5%时的PDOS图。图8(a)中主要包含了4条曲线分别代表了完美、0.1%、0.3%和0.5%缺陷浓度的SVSLG 的PDOS。4 条曲线具有相似的变化趋势，在低频区域内(12～14 THz)都包含有一个波峰，在高频区域内(45～50 THz)都包含一个最大的波峰。进一步观察发现，低频区域内4条曲线的波峰按照缺陷浓度的增加依次按照下降的趋势排列，完美SLG的PDOS低频区域内峰值最大。图8(b)同样包含了4条曲线关于完美、0.1%、0.3%和0.5%缺陷浓度DVSLG 的PDOS。图中曲线变化趋势与图8(a)相似，唯一的区别在于0.5%DVSLG 在低频区域内的波峰值大于0.3%DVSLG 的峰值，但是0.3%DVSLG 低频区域波峰左侧峰峰值大于0.5%DVSLG左侧峰峰值。

图8 不同缺陷浓度和不同缺陷类型的SLG的PDOSFig.8 PDOS of(a)SV and(b)DV defect SLG with different defect concentrations

通过SLG 的声子色散图[29]了解到，SLG 具有3 个声学支(acoustic phonon)和3 个光学支(optical phonon)包括：平面内纵向声学声子(longitudinal acoustic，LA)和 光 学 声 子(longitudinal optical，LO)；平面内横向声学声子(transverse acoustic，TA)和光学声子(transverse optical，TO)；以及垂直平面方向的声学声子(out-of-plane acoustic，ZA)和光学声子(out-of-plane optical，ZO)。并且高频部分主要是光学支的贡献，而低频部分主要是声学支的贡献。计算声子对热导率的贡献，只需要关注声子色散图的低频曲线。前人通过加权态密度研究发现SLG 导热时高频声子所占比重很小，低频声学声子具有绝对优势，因此低频声子对热导率贡献较大[31]。在SV 缺陷下，随着缺陷浓度的增加波峰峰值不断下降。根据经典的晶格传热理论，PDOS中波峰的峰值显著降低，这表明缺陷导致波峰软化，波峰的软化能说明原子间结合强度减弱，声子速度降低，低频声子的数量增加，导致热导率降低。该原理解释了图7 中随着SV 缺陷浓度的增加SLG 热导率在不断减小。图8(b)可看出，DV 缺陷具有与SV 缺陷同样的效果，缺陷浓度的增加导致了波峰的下降。虽然0.5%DVSLG在低频区域的波峰峰值大于0.3%DVSLG，但是0.5%DVSLG 低频峰的左侧峰峰值仍然小于0.3%DVSLG的左侧峰的峰值，对比之后得到低频区域内0.3%DVSLG低频声子的数量仍比0.5%DVSLG 多。最终得到DV缺陷下随着缺陷浓度的增加SLG热导率不断减小。

2.3 温度对SLG热导率的影响

模拟温度对固定尺寸W为6.41 nm，L为20.51 nm SLG 热导率的影响，分别计算了在300、400、500、600和700 K等温度下，完美、0.3%SV和0.3%DV 3种类型SLG体系的热导率。图9为完美、0.3%SV和0.3%DV缺陷的SLG在300～700 K温度下的热导率和相对热导率，此时相对热导率的定义为某一种类型SLG 体系在某一温度下的热导率与同类型SLG体系在300 K时热导率的比值。

图9(a)包含3条曲线，分别为完美、0.3%SV和0.3%DV缺陷的SLG的热导率，且曲线都随着温度的增加不断下降。其中温度从300 K增加到700 K，完美SLG 的热导率下降趋势最明显，该模型在700 K 时的热导率为239.3 W/(m·K)，等于该模型在300 K 时热导率的50.0%。曲线0.3%SVSLG 和0.3%DVSLG 的热导率变化趋势相似，都是随着温度增加缓慢下降，相比完美SLG 的热导率曲线，两条曲线随温度的变化趋势更平缓。进一步对比0.3%SVSLG与0.3%DVSLG的热导率曲线的变化。温度从300 K 增加到700 K，0.3%SVSLG 的热导率为115.9 W/(m·K)，热导率减少了48.3 W/(m·K)；0.3%DVSLG 热导率为144.5 W/(m·K)，热导率减少了51.8 W/(m·K)。很明显看出，DVSLG 的热导率的减小量大于SVSLG 的热导率减小量，但是相同温度下DVSLG 的热导率总是大于SVSLG 的热导率。

图9 温度对完美SLG，0.3%SV和0.3%DV缺陷SLG热导率和相对热导率的影响Fig.9 Effects of temperature on thermal conductivity and relative thermal conductivity of perfect SLG,0.3%SV,and 0.3%DV defect SLG

图9(b)中包含3条曲线，分别为完美、0.3%SV和0.3%DV缺陷的SLG的相对热导率曲线，曲线都随着温度升高快速下降，其中下降最快的是完美SLG 曲线，另外两条曲线随着温度的增加，相对热导率的下降趋势较为平缓。两条平缓曲线中，0.3%DVSLG的下降趋势最为平缓，0.3%DVSLG模型在700 K 时的相对热导率相比该模型在300 K 时的相对热导率只减少了29.4%；然而0.3%SVSLG模型在700 K 时的相对热导率相比该模型在300 K时的相对热导率减小了28.5%，此减小量明显大于0.3%DVSLG模型的相对热导率减少量。与文献[20]计算的SLG 相对热导率随温度的变化规律相似，温度从300 K 增加到1000 K 时，前人计算得到的0.1%SVSLG相对热导率减少了20%，稍小于本文0.3%SVSLG 相对热导率的减小量28.5%。考虑到缺陷浓度不同本身也会影响计算结果，两个相对热导率变化量之间差异并不大，研究结果具有一定的可靠性。

完美SLG 的热导率随着温度的上升不断减小，由于温度上升使得内部声子发生边界散射同时声子的热输运变得更加无序，进而导致SLG的λ值减小热导率降低。SLG 中缺陷的存在首先导致SLG 内部大量声子发生散射，此时随着温度的升高进一步激发了SLG 内部的声子散射。由于缺陷的存在导致温度激发的声子散射减少，0.3%SVSLG 和0.3%DVSLG 的热导率随着温度的增加出现了缓慢下降的趋势。对比0.3%DVSLG，0.3%SVSLG 中包含的缺陷中心更多，声子散射更多，因而导致0.3%SVSLG 中温度激发的声子散射量会更小，其热导率的减少量更少。由于缺陷造成的声子散射远大于温度影响下的声子散射数量，0.3%SVSLG 内部包含的声子散射总量还是最多的。温度相同且缺陷浓度固定为0.3%时，受SV 缺陷调制的SLG 内部包含的声子散射总量多于DV缺陷内部声子散射，因此DVSLG 热导率较大。当温度从300 K 升高到700 K，而缺陷浓度为0.3%时，由于受DV 缺陷调制的SLG的相对热导率减少量低于SV缺陷的相对热导率减少量，所以受DV缺陷调制的SLG的相对热导率受温度的影响更小。

3 结 论

本文使用NEMD 方法计算了尺寸、缺陷等对SLG 的热导率的影响。考虑到实际环境因素复杂性，研究了缺陷浓度、空位缺陷(SV、DV)和温度对SLG热导率的影响，得出的结论为：SLG热导率具有尺寸效应，SLG在300 K时的热导率随着宽度和长度的增加都会不断增大，同时长度对于SLG热导率的增加影响更大。拟合计算得到宽度为10.5 nm时，无限长SLG的热导率为2667.6 W/(m·K)。当温度为300 K时，SLG的热导率随着缺陷浓度0.1%增加到0.5%而急剧减小，并且SV、DV 缺陷对SLG热导率影响基本相似，两者之间的差异不大。相比0.5%SV 缺陷浓度对SLG 的热导率影响，0.5%DV缺陷浓度导致完美SLG的热导率仅降低27.7%，热导率数值减小了345.7 W/(m·K)。SLG 的热导率随着缺陷浓度的增加先急剧下降，当缺陷浓度达到了0.2%后热导率对缺陷浓度的变化不敏感。PDOS的研究得到随着SV与DV缺陷浓度的增加，在低频区域内的波峰峰值随着缺陷浓度的增加峰值不断减小，SLG中低频声子数量在下降。SLG热导率由低频声子主导，低频声子减少导致了SLG 的热导率的减小。温度从300 K升高到700 K，完美SLG模型的热导率快速下降，该模型在700 K 时的热导率为239.3 W/(m·K)，仅为该模型在300 K 时热导率的50.0%；对于缺陷体系而言，温度从300 K 升高到700 K，0.3%DVSLG与0.3%SVSLG的热导率受温度的影响相比完美SLG较小。0.3%DVSLG模型在700 K时的热导率为144.5 W/(m·K)，热导率减小量为该模型在300 K时热导率的26.4%；0.3%SVSLG模型在700 K 时的热导率为115.9 W/(m·K)小于0.3%DVSLG 的热导率，热导率减少量为该模型在300 K时热导率的28.5%>26.4%，因此缺陷浓度为0.3%时，DVSLG 相比SVSLG 热导率受温度的影响较小，热导率的变化相对稳定。本文研究表明，通过改变SLG 缺陷类型及缺陷浓度可以有效控制SLG 的热导率，这将为SLG 基纳米器件在热管理中的应用提供一定的理论参考。