基于稀疏信号重构的DOA和极化角度估计算法
2016-08-09练秋生
田 野,练秋生,徐 鹤
(燕山大学信息科学与工程学院,河北秦皇岛 066004)
基于稀疏信号重构的DOA和极化角度估计算法
田野,练秋生,徐鹤
(燕山大学信息科学与工程学院,河北秦皇岛 066004)
现有的波达方向(Direction Of Arrival,DOA)和极化参数估计方法大多基于子空间理论.本文从稀疏信号重构角度出发,提出了一种新的DOA和极化角度估计算法.该算法首先构建一个只包含DOA信息的累积量矩阵模型,然后基于加权l1范数最小化获得DOA估计.在DOA估计的基础上,进一步通过求和平均运算构建三个包含不同极化信息的累积量向量模型,利用Zhang惩罚进行稀疏性约束,获得近似无偏的极化角度估计.阐述了如何利用极化信息来区分两个入射角度一样的信源信号.计算机仿真结果验证了所提算法的有效性.
DOA和极化角度估计;稀疏信号重构;加权l1范数;Zhang惩罚
1 引言
波达方向(Direction Of Arrival,DOA)估计是阵列信号处理领域的核心研究内容之一,它在智能天线、无线通信、雷达、声呐、电子侦查及地震勘探等领域有着广泛的应用前景[1],受到了国内外学者的广泛关注,各种适用于DOA估计的算法被相继提出[2~5].这些算法均基于标量传感器阵列,它们不能充分利用EM信源信号的极化信息.
在无线通信和雷达领域,极化敏感阵列已被证明可以获得比标量传感器更多的优势[6,7].鉴于这一事实,一些适用于DOA和极化参数估计的算法也被提出,包括矢量叉积算法[8],极化类ESPRIT算法[9~11],极化四元数MUSIC算法[12,13],极化双模MUSIC算法[14],极化MODE算法[15]等.上述算法大都基于子空间理论,由于理论框架的限制其分辨率性能有限,且不能充分利用信号的极化信息.
近年来,稀疏信号重构作为一种新的理论框架逐渐被引入到DOA估计领域.目前已出现的稀疏信号重构类DOA估计算法主要包括l1范数惩罚算法[16]、加权l1范数惩罚算法[17,18]、l0范数逼近算法[19,20]以及迭代重加权最小范数算法[21]等.和传统子空间类DOA估计算法相比,稀疏信号重构类算法具有分辨率高、噪声鲁棒性好、无需精确的初始条件等优势.然而值得注意的是,现有的稀疏重构类DOA估计算法大都存在估计偏的问题[22],这在一定程度上影响了参数估计性能,并严重制约其向极化敏感阵列的拓展.
为了充分利用EM信号的极化信息并克服现有稀疏信号重构类DOA估计算法存在的共性问题,本文借助COLD(Concentered Orthogonal Loop and Dipole)阵列,提出了一种新的基于稀疏信号重构的DOA和极化角度估计算法.该算法步骤如下:(1)构建累积量矩阵并基于加权l1范数最小化获得DOA估计;(2)通过求和平均运算构建三个特殊的累积量向量,利用Zhang惩罚进行稀疏性约束获得极化角度估计;(3)利用估计的极化信息判断是否有两个信源从相同的方向入射到阵列.最后通过仿真实验验证了所提算法的有效性.
2 极化远场源模型
考虑K个完全极化远场窄带信号入射到一个由L=2M+1个COLD阵元组成的均匀线阵上.如图1所示,其第m(m=-M,…,M)个阵元以间距d均匀分布在y轴上.偶极子平行于z轴,电磁环平行于x-y平面.椭圆极化方式下的电场输出可表示为
E=Eθθ+Eφφ
(1)
式(1)中,Eθ代表水平分量,Eφ代表垂直分量,θ和φ分别代表沿方位角θ和俯仰角φ的球面单位向量.对于给定的信号极化,电场分量可进一步表示为
Eθ=E0cos(γ),
Eφ=E0sin(γ)ejη
(2)
式(2)中,E0代表非零复信号幅度,γ∈[0,π/2)和η∈[-π,π]分别代表信号的极化角度和极化相位差.

基于式(1)和式(2),得到入射信号的电场和磁场分别为
E=Eθθ+Eφφ=E0[cos(γ)θ+sin(γ)ejηφ]
(3)
H=Eθφ-Eφθ=E0[cos(γ)φ-sin(γ)ejηθ]
(4)
为方便且不失一般性,假设天线和入射信号是共面的,即φ=90°,则式(3)和式(4)可重新表示为
E=E0[cos(γ)(-sin(θ)x+cos(θ)y)-sin(γ)ejηz]
(5)
H=E0[sin(γ)ejη(sin(θ)x-cos(θ)y)-cos(γ)z]
(6)
其中,x,y和z分别代表沿x,y,z方向的单位向量.

(7)
(8)

以第0个阵元为相位参考点,阵列输出可表示为
u[l](t)=As[l](t)+n[l](t)
(9)
u[d](t)=As[d](t)+n[d](t)
(10)
其中
(11)
(12)
s[l](t)=-[s1(t)cos(γ1),…,sK(t)cos(γK)]T
(13)
s[d](t)=-[s1(t)sin(γ1)ejη1,…,sK(t)sin(γK)ejηK]T
(14)
(15)
(16)
其中,上标T代表转置操作,A=[a(θ1),…,a(θK)]代表L×K的阵列流型矩阵,其第k列代表第k个信号的导向矢量
a(θk)=[e-jMωk,…,1,…,ejMωk]T
(17)
为保证参数估计的唯一性,本文做如下假设:
[A1]信源信号{s1(t),…,sK(t)}为窄带、统计独立过程且其四阶累积量非零;
[A2]噪声分量n[l](t)和n[d](t)为加性统计独立高斯过程,且与信源信号不相关;
[A3]为避免相位模糊,阵元间距和信源数分别满足d≤λ/2,K 3.1DOA估计 为抑制高斯噪声并保证估计精度,本文基于阵列输出数据分别构建L×L3的自极化和互极化累积量矩阵,表示为 (18) (19) (20) (21) 为获得更好的估计结果,定义 (22) 式(22)说明信源信号在累积量域已被完全接收,这直接保证了算法的DOA估计精度.同时由于矩阵C只包含信源的DOA信息,因此DOA估计性能将不受极化参数的影响. 矩阵C的列向量cp,q,n可表示为 (23) 式(23)中,sp,q,n代表K×1的向量 (24) (25) (26) 式(26)中,X是包含所有列向量xp,q,n的矩阵.假定信源数K已知或已通过AIC或MDL准则准确估计[23],则可通过对矩阵C进行奇异值分解(Singular Value Decomposition,SVD)来降低计算复杂度,得到 (27) 其中,C=ULVH,CSV=CVDK,XSV=XVDK,DK=[IK,0]T,IK代表K×K的单位矩阵,0代表K×(L3-K)的零值矩阵.上标H代表共轭转置操作. (28) (29) (30) (31) (32) (33) 和获得式(22)类似,定义 (34) 式(34)的矩阵形式为 Cw=AC4sAH (35) (36) (37) 优化问题(37)可直接通过内点法二阶锥规划(SOCP)[24]进行求解,其标准形式为 s.t. (38) 3.2极化角度估计 为获得极化角度估计,本文构建三个特殊的累积量向量,分别表示为式(39)~(41). (39) (40) (41) 向量c1到c3的稀疏表示为 (42) (43) (44) (45) (46) (47) (48) 证明当只有一个信源信号由方向θ入射到阵列时,有 ρk=cos4(γ)sin4(γ)-(cos2(γ)sin2(γ))2=0 (49) 当有两个信源信号由相同的方向θ入射到阵列时,有式(50). ρk=[(cos4(γ1)+cos4(γ2))(sin4(γ1)+sin4(γ2)) -(cos2(γ1)sin2(γ1)+cos2(γ2)sin2(γ2))2] =cos4(γ1)sin4(γ2)+cos4(γ2)sin4(γ1) -2cos2(γ1)sin2(γ1)cos2(γ2)sin2(γ2) =(cos2(γ1)sin2(γ2)-cos2(γ2)sin2(γ1))2 =sin2(γ2+γ1)sin2(γ2-γ1) (50) 由于γ∈[0,π/2),并且γ1和γ2不同,则γ1+γ2∈(0,π),γ1-γ2∈(-π/2,0)∪(0,π/2),因此1>ρk>0,并且ρk随着γ1→π/2,γ2→0或γ2→π/2,γ1→0而趋于最大值1.证毕. 注1:定理1说明当极化角度不同时,本文所提算法可有效地区分两个入射角度相同的信源信号,并且区分性能随着γ1→π/2,γ2→0或γ2→π/2,γ1→0而变好. 注2:本文极化参数估计的目的是为了在极化域区分两个入射角度相同的信源信号,由于在实施过程中只依靠极化角度即可完成区分(见定理1),故本文未进行极化相位差的估计. 3.3算法步骤 本文所提算法步骤可总结如下: 步骤1构建累积量矩阵C,Cw及累积量向量ck; 步骤3对矩阵Cw进行奇异值分解,并利用信号子空间与噪声子空间的正交性构建权值矩阵w; 步骤4基于加权l1范数最小化方法和SOCP获得DOA估计; 步骤5借鉴Zhang惩罚思想,在LASSO估计初值的基础上,利用式(45)进行稀疏信号重构获得极化角度估计; 步骤6通过ρk的值判断是否有两个信源信号由相同的方向入射到阵列. (51) 本章通过仿真实验验证所提算法的性能,并与交叉偶极子阵下最具代表性的ESPRIT算法和COLD阵下的MUSIC算法以及MODE算法进行比较.仿真中采用由7个阵元组成的均匀线阵,阵元间距d=λ/2,入射信号功率相等,建模为ejζt,其中相位ζt均匀分布在[0,2π].除实验3外,噪声均假定为高斯白噪声.以1°间隔先对-90°到90°的空间进行粗网格划分,进而在估计出的角度周围逐步细化网格.DOA估计的均方根误差(RMSE)通过500次独立的Monte Carlo仿真实验获得,定义为 (52) 实验1角度分辨率性能比较 为展示本文所提算法的角度分辨率性能,考虑两个空间间隔很近的信源信号入射情况,入射角度分别为θ1=25°,θ2=30°,相对应的极化参数(γ,η)分别为(20°,0°)和(60°,0°).SNR=5dB,快拍数为500条件下的空间谱输出如图2(a)所示,可以看到本文所提算法和MUSIC算法均能分辨两个信源信号.然而当把SNR降为-5dB时,如图2(b)所示,只有本文所提算法仍能很好地区分两个信源信号,而MUSIC算法则模糊了两个信号的谱峰.这说明本文所提算法具有更高的分辨率特性. 实验2高斯白噪声下角度估计性能比较 考虑两个窄带不相关信源DOA估计情况,入射角度分别为θ1=-10°,θ2=30°,相对应的极化参数与实验1相同.DOA估计均方根误差随SNR和快拍数的变化关系分别如图3(a)和图3(b)所示.可以看出,本文所提算法的DOA估计性能虽然略低于MODE算法,但在整个SNR和采用快拍数域全面优于ESPRIT算法.同时需要说明的是,MODE算法需要一个较好的初始估计才能保证全局最优性,而本文所提算法由于基于凸优化理论框架,无需较好的初始条件. 实验3高斯色噪声下角度估计性能分析 除背景噪声假定为高斯色噪声外,其它实验条件与实验2相同.噪声协方差矩阵N的第(i1,i2)个元素为 (53) 实验4两种特殊入射情况下的估计结果 考虑两种特殊的信源信号入射情况,即(1)入射角度不同,极化参数相同;(2)入射角度相同,极化角度不同.SNR=10dB,快拍数为1000下10次独立的仿真结果分别如图5(a)和图5(b)所示.图5(a)中三个信源的入射角度分别为θ1=-10°,θ2=30°,θ3=45°,极化参数(γ,η)均为(30°,0°),可以看出信号入射角度不同时本文算法不仅可以很容易地区分三个信源信号,而且可以获得很好的极化角度估计.图5(b)中三个信源的入射角度分别为θ1=-10°,θ2=30°,θ3=30°,相对应的极化参数(γ,η)为(30°,0°),(45°,0°)和(0°,0°).可以看出,虽然图5(b)中只出现了两个信源位置信息,但我们发现ρ1≪ρ2=0.2480,这说明在极化角度不同时,即便两个信源的入射角度一致,所提算法仍能有效地区分它们.换句话说,本文算法可以更好的利用极化信息,这是其它算法无法比拟的. 本文在稀疏信号重构理论框架下提出了一种新的DOA和极化角度估计算法.该算法在累积量域构建稀疏表示模型,并分别基于加权l1范数最小化和Zhang惩罚策略实现高斯白/色噪声下的DOA和极化角度估计.借助估计的极化角度信息,该算法还可以有效区分两个入射角度一样的信源信号.计算机仿真实验验证了所提算法的有效性,并展示了其在分辨率、色噪声下估计精度等方面的优势. [1]Krim H,Viberg M.Two decades of array signal processing research:the parametric approach[J].IEEE Signal Processing Magazine,1996,13(4):67-94. [2]Yaqoob M A,Mannesson A,Bemhardsson B,et al.On the performance of random antenna arrays for direction of arrival estimation[A].Proceedings of the 2014 IEEE International Conference on Communications Workshops (ICC)[C].USA:IEEE Press,2014.193-199. [3]Qian C,Huang L,So H C.Improved unitary root-MUSIC for DOA estimation based on pseudo-noise resampling[J].IEEE Signal Processing Letters,2014,21(2):140-144. [4]Xi N,Li L.A computationally efficient subspace algorithm for 2-D DOA estimation with L-shaped array[J].IEEE Signal Processing Letters,2014,21(8):971-974. [5]Gou X,Liu Z,Xu Y.Biquaternion cumulant-MUSIC for DOA estimation of noncircular signals[J].Signal Processing,2013,93(4):874-881. [6]Manikas A,Ng J W.Cross-dipole arrays for asynchronous DS-CDMA systems[J].IEEE Transactions on Antennas and Propagation,2004,52(1):122-131. [7]Giuli D.Polarization diversity in radars[J].Proceedings of the IEEE,1986,74(2):245-269. [8]Nehorai N,Paldi E.Vector-sensor array processing for electro-magnetic source localization[J].IEEE Transactions on Signal Processing,1994,42(2):376-398. [9]Li J,Compton Jr R T.Angle and polarization estimation using ESPRIT with a polarization sensitive array[J].IEEE Transactions on Antennas and Propagation,1991,39(9):1376-1383. [10]Lin C,Fang W,Yang W,et al.SPS-ESPRIT for joint DOA and polarization estimation with a COLD array[A].Proceedings of the IEEE International Symposium on Antennas and Propagation[C].USA:IEEE Press,2007.1136-1139. [11]齐子森,郭英,姬伟峰,等.锥面共形阵列天线盲极化DOA估计算法[J].电子学报,2009,37(9):1919-1925. Qi Zi-sen,Guo Ying,Ji Wei-feng,et al.Blind DOA estimation algorithm for conical conformal array antenna with respect to polarization diversity[J].Acta Electronica Sinica,2009,37(9):1919-1925.(in Chinese) [12]Miron S,Le B N,Mars J I.Quaternion-MUSIC for vector-sensor array processing[J].IEEE Transactions on Signal Processing,2006,54(4):1218-1229. [13]Le B N,Maron S,Mars J I.MUSIC algorithm for vector-sensors array using biquaternions[J].IEEE Transactions on Signal Processing,2007,55(9):4523-4533. [14]龚晓峰,等.电磁矢量传感器阵列信号波达方向估计:双模MUSIC[J].电子学报,2008,36(9):1698-1703. Gong Xiao-feng,et al.Direction-finding with electromagnetic vector-sensor array:dual-mode MUSIC[J].Acta Electronica Sinica,2008,36(9):1698-1703.(in Chinese) [15]Li J,Stoica P,Zheng D.Efficient direction and polarization estimation with a COLD array[J].IEEE Transactions on Antennas and Propagation,1996,44(4):539-547. [16]Malioutov D,et al.A sparse signal reconstruction perspective for source localization with sensor arrays[J].IEEE Transactions on Signal Processing,2005,53(8):3010-3022. [17]Xu X,Wei X H,Ye Z F.DOA estimation based on sparse signal recovery utilizing weighted l1-norm penalty[J].IEEE Signal Processing Letters,2012,19(3):155-158. [18]田野,孙晓颖,秦宇镝.基于两步加权L1范数约束的高分辨率波达方向和功率估计[J].电子与信息学报,2014,36(7):1637-1641. Tian Ye,Sun Xiao-ying,Qin Yu-di.High-resolution direction-of-arrival and power estimation using two-stage weighted L1penalty[J].Journal of Electronics & Information Technology,2014,36(7):1637-1641.(in Chinese) [19]Hyder M M,Mahata K.Direction-of-arrival estimation using a mixed l2,0norm approximation[J].IEEE Transactions on Signal Processing,2010,58(9):4646-4655. [20]Tian Y,et al.DOA and power estimation using a sparse representation of second-order statistics vector and l0-norm approximation[J].Signal Processing,2014,105:98-108. [21]Gorodnitsky I F,Rao B D.Sparse signal reconstruction from limited data using FOCUSS:A re-weighted minimum norm algorithm[J].IEEE Transactions on Signal Processing,1997,45(3):600-616. [22]Gasso G,Rakotomamonjy A,Canu S.Recovering sparse signals with a certain family of non-convex penalties and DC programming[J].IEEE Transactions on signal processing,2009,57(12):4686-4698. [23]Wax M,Kailath T.Detection of signals by information theoretic criteria[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1985,33(2):387-392. [24]Nemirovski A,Ben T A.Lectures on Modern Convex Optimization:Analysis,Algorithms and Engineering Applications[M].Philadelphia,PA:SIAM,2001. [25]Zhang T.Some sharp performance bounds for least squares regression with l1regularization[J].Annals of Statistics,2009,37(5A):2109-2144. [26]Shao J.Linear model selection by cross-validation[J].Journal of the American Statistical Association,1993,88(422):486-494. 田野男,1985年12月生于河北省平泉县,2014年于吉林大学通信与信息系统专业获得博士学位,现为燕山大学信息科学与工程学院讲师,主要研究方向为阵列信号处理、稀疏信号重构等. E-mail:tianye@ysu.edu.cn 练秋生男,1969年8月生于江西遂川,工学博士,现为燕山大学信息科学与工程学院教授、博士生导师,主要研究方向为稀疏表示、压缩感知等. E-mail:lianqs@ysu.edu.cn 徐鹤女,1989年12月生于辽宁省丹东市,2013年于吉林大学通信与信息系统专业获硕士学位,主要研究方向为阵列信号处理、空间谱估计等. E-mail:xuhebest@sina.com DOA and Polarization Angle Estimation AlgorithmBased on Sparse Signal Reconstruction TIAN Ye,LIAN Qiu-sheng,XU He (School of Information Science and Engineering,Yanshan University,Qinhuangdao,Hebei 066004,China) Existing direction-of-arrival and polarization estimation methods mostly rely on subspace technique.This paper proposes a novel DOA and polarization angle estimation algorithm from sparse signal reconstruction perspective.The algorithm first constructs a cumulant matrix model which is only related to DOA parameter,and then obtains DOA estimation using the weighted l1-norm minimization.Further,this paper constructs another three cumulant vector models by sum-average arithmetic,and enforces sparsity by Zhang penalty,which leads to almost unbiased polarization angle estimation.Meanwhile,this paper also demonstrates how to identify two sources with same DOA using their polarization characteristics.Computer simulation results validate the effectiveness of the proposed algorithm. DOA and polarization angle estimation;sparse signal reconstruction;weighted l1-norm;Zhang penalty 2015-01-28; 2015-04-08;责任编辑:孙瑶 国家自然科学基金(No.61471313);河北省高等学校青年拔尖人才计划(No.BJ2016051);燕山大学校内自主研究课题(No.14LGA012);燕山大学博士基金(No.B887) TN911.7 A 0372-2112 (2016)07-1548-07 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.07.0043 DOA和极化角度估计算法


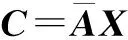




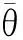


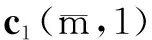







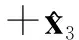



4 仿真与分析



5 结论



