基于增长修剪型神经网络的半导体生产线动态瓶颈分析方法

曹政才，邱明辉，刘　民

(1.北京化工大学信息科学与技术学院，北京 100029； 2.吉林大学符号计算与知识工程教育部重点实验室，吉林长春 130012； 3.清华大学自动化系，北京 100084)

基于增长修剪型神经网络的半导体生产线动态瓶颈分析方法

曹政才1,2，邱明辉1,2，刘民3

(1.北京化工大学信息科学与技术学院，北京 100029； 2.吉林大学符号计算与知识工程教育部重点实验室，吉林长春 130012； 3.清华大学自动化系，北京 100084)

瓶颈设备是制约半导体生产线在制品水平、生产周期及准时交货率的关键因素，对其进行有效地分析能够提高生产线多性能.现有的分析方法主要是将瓶颈设备视为静态瓶颈，未考虑到生产线不确定因素所带来的动态漂移问题，这样容易造成以瓶颈设备控制为核心的调度算法缺乏柔性，降低算法实效性，因此，本文提出一种基于增长修剪型神经网络的动态瓶颈分析方法.该方法从设备相对生产负荷、利用率及缓冲区队列长度等方面，利用复合定义方法描述设备的综合瓶颈度，并结合瓶颈判定机制识别瓶颈；其次，通过构建增长修剪型神经网络模型预测生产线下一时刻瓶颈，借鉴闭环控制思想动态修正网络结构；再次，使用单因子试验法对影响瓶颈的关键参数进行分析以获得设备动态特性；最后，通过仿真验证方法的可行性和有效性.

半导体生产线；动态瓶颈分析；综合瓶颈度；增长修剪型神经网络；单因子试验法

1　引言

半导体制造业是一个资金密集型的高科技产业，对经济发展具有重大贡献，为继续保持半导体制造业发展的良好势头和提升市场竞争力，不仅要扩大规模而且要提高生产效率[1].半导体生产线被认为是当今最为复杂的制造系统，具有多重入、大规模、多产品、不确定及混合加工等特点，其优化调度问题已成为学术界及工程界研究的热点.瓶颈问题是半导体生产线优化调度的关键问题，瓶颈设备成为制约系统产量、生产周期和准时交货率的关键因素[2,3].因此，对瓶颈设备进行有效分析有助于提升半导体制造业的绩效指标.

目前国内外针对瓶颈的研究，主要有①瓶颈识别：文献[4～6]利用生产线设备或缓冲区的单一性能指标(如：设备利用率、相对生产负荷和缓冲区在制品队列长度等)对设备进行识别；Li等人[7]通过长短期的生产数据信息驱动对生产线瓶颈设备的识别；文献[8]构建一种基于改进的自适应模糊推理系统的预测模型，综合利用生产线上数值型和符号型的相关生产信息识别并预测瓶颈设备.②瓶颈漂移现象分析：文献[9]对瓶颈漂移现象进行了研究，提出使用线性回归方法确定瓶颈漂移，通过仿真方法验证了可通过工件准时交货率、加工时间等参数预测瓶颈；文献[10]对影响瓶颈漂移的不确定因素进行分析，提出采用马尔科夫链方法分析各个因素之间的耦合机理关系，并给出了瓶颈漂移因素对设备生产能力和生产负载的综合贡献函数，定量分析瓶颈设备.

针对上述研究，为了有效解决以静态瓶颈为中心制定的调度策略缺乏柔性的问题，本文提出一种基于增长修剪型神经网络的动态瓶颈分析方法.如图1所示，该方法利用复合定义法从生产线的多个性能角度考虑对瓶颈设备的影响，并基于GPNN构建瓶颈预测模型，利用闭环控制思想动态修正网络结构，使用单因子分析方法对不确定生产环境下的动态瓶颈进行分析.

2　基于复合定义法的瓶颈设备识别

瓶颈设备是影响SWFS绩效指标的重要因素，对其进行准确有效的识别有助于下一步分析.针对传统方法仅利用单参数进行识别瓶颈设备的缺陷，复合定义法给出从设备相对生产负荷、利用率及缓冲区队列长度等生产线性能角度定义设备的综合瓶颈度识别瓶颈.该方法从多个角度描述设备属性，能够有效地侦测瓶颈设备.

2.1设备综合瓶颈度

综合瓶颈度是描述设备成为瓶颈可能性的指标，在以瓶颈为中心的半导体生产线控制与决策过程中具有重要意义.设备综合瓶颈度度量指标体系如下.

2.1.1设备相对生产负荷

瓶颈设备产出率决定着半导体产出率，而设备产出率则受设备生产负荷和生产能力影响.设备相对生产负荷越大则意味着设备对生产影响越大，其成为瓶颈的可能性也就越大.设备相对生产负荷WLm(t)如式(1)所示：

(1)

其中，M为生产线上设备数；NT为生产线工件类总数；Ni为工件i的加工工序步数；qi为在设备m上等待加工的i工件数量；tijm为工件i的第j道工序在设备m上的加工时间；θijm为加工系数；Tm为时间窗内设备m有效加工时间；Δpm,i为不合格品i在设备m上返修时间；μijm为设备的加工能力系数.

2.1.2设备利用率

在SWFS中，设备的工作状态分为等待、正常运行、阻塞和故障.其中，设备的正常运行和阻塞状态为设备的正常工作时间.单位时间内，设备由以上四种工作状态组成，其利用率Um(t)定义如下：

T=Twm(t)+Tsm(t)+Tfm(t)+Tbm(t)

(2)

(3)

其中，参数Twm(t)、Tsm(t)、Tfm(t)及Tbm(t)分别为设备的正常运行时间、饥饿时间、故障时间和等待时间；T为划定的单位时间长度.

2.1.3缓冲区队列长度

设备缓冲区工件队列长度不仅间接反映设备对系统生产率的制约程度，而且也影响工件加工周期.因此，工件队列长度Lm(t)成为指示设备瓶颈程度的关键参数.文献[7]提出一种动态瓶颈指数识别算法，并通过指数映射变换得到设备的瞬时瓶颈度LLm(t)，如式(4)所示：

LLm(t)=1-e-Lm(t)/L

(4)

其中，L为设备缓冲区最大容量；Lm(t)为缓冲区工件数.

上述生产线特征分别从设备负荷量、工件待加工数及工作状态等三个不同方面表征对系统的影响.文献[7]提出的设备综合瓶颈指数分别从内部和外部两方面表征设备当前的加工状态.设备内部特征指数am(t)和外部特征指数bm(t)如式(5)、(6)所示：

am(t)=WLm(t)

(5)

bm(t)=LLm(t)+Um(t)

(6)

设备的综合瓶颈指数BNIm(t)定义如式(7)所示：

BNIm(t)=w1am(t)+w2bm(t)

(7)

其中，w1和w2分别是内部特征指数am(t)和外部特征指数bm(t)相对应的权值.

2.2基于综合瓶颈指数的瓶颈设备识别

通过上述定义，综合瓶颈指数越大的设备成为瓶颈的可能性也就越大.但是对于瓶颈和非瓶颈设备并没有一个明显的划分，于是，根据实际生产经验可设立一个阈值以划分设备.其数学模型定义如式(8)所示：

(8)

其中，S表示系统中所有设备集合；SBN(t)表示t时刻系统瓶颈设备集合，其中BNIm(t)最大的设备为主瓶颈，其次为次瓶颈；SnBN(t)表示t时刻系统非瓶颈设备的集合；k为划分瓶颈设备的阈值，ν≤k≤1，ν根据生产线的稳定性进行设定(一般不宜取太小，以防止将非瓶颈误判为瓶颈；同时也不能取太大，以防止瓶颈的漏判).

3　基于增长修剪型神经网络的瓶颈预测动态模型

目前瓶颈预测模型的网络结构一般是固定的，结构过大或过小都会影响神经网络预测的最终性能.为了寻求满足SWFS瓶颈设备预测要求的网络结构，本文提出利用傅立叶变换的敏感度分析方法进行网络结构的合理性评价，以此为依据实施隐含层神经元数目、权值的优化，构建生产线GPNN瓶颈设备预测模型，并且该模型结合闭环控制思想，能够依据生产线动态变化情况实时修正网络结构，实现准确、有效的预测.

3.1构建基于增长修剪型神经网络的瓶颈预测模型

利用GPNN构建瓶颈预测模型，该模型基于误差反向传播算法构建，模型为三层网络结构：输入层、单隐含层、输出层.初始化相关参数：隐含层神经元节点数J(由经验公式获得)、层间连接权值w和阈值采用随机概率赋值.隐含层节点数J由经验公式[11]计算得到：

(9)

其中，nI为模型输入层节点数；nO为模型输出层节数；C为经验常数.构建预测模型的误差函数定义为：

(10)

其中，M为训练数据样本数；ym(t)为神经网络模型第m次训练时的实际输出；yd(t)为模型的期望输出.

如图2所示，基于Levenberg-Marquardt(LM)算法对预测模型进行训练，使得模型预测误差函数值达到期望值ed；训练过程中，利用傅立叶变换的敏感度分析方法对模型隐含层神经元进行敏感度分析，删除冗余神经元、分裂负载过大的神经元，实现隐含层结构的动态优化.训练的主要步骤为：

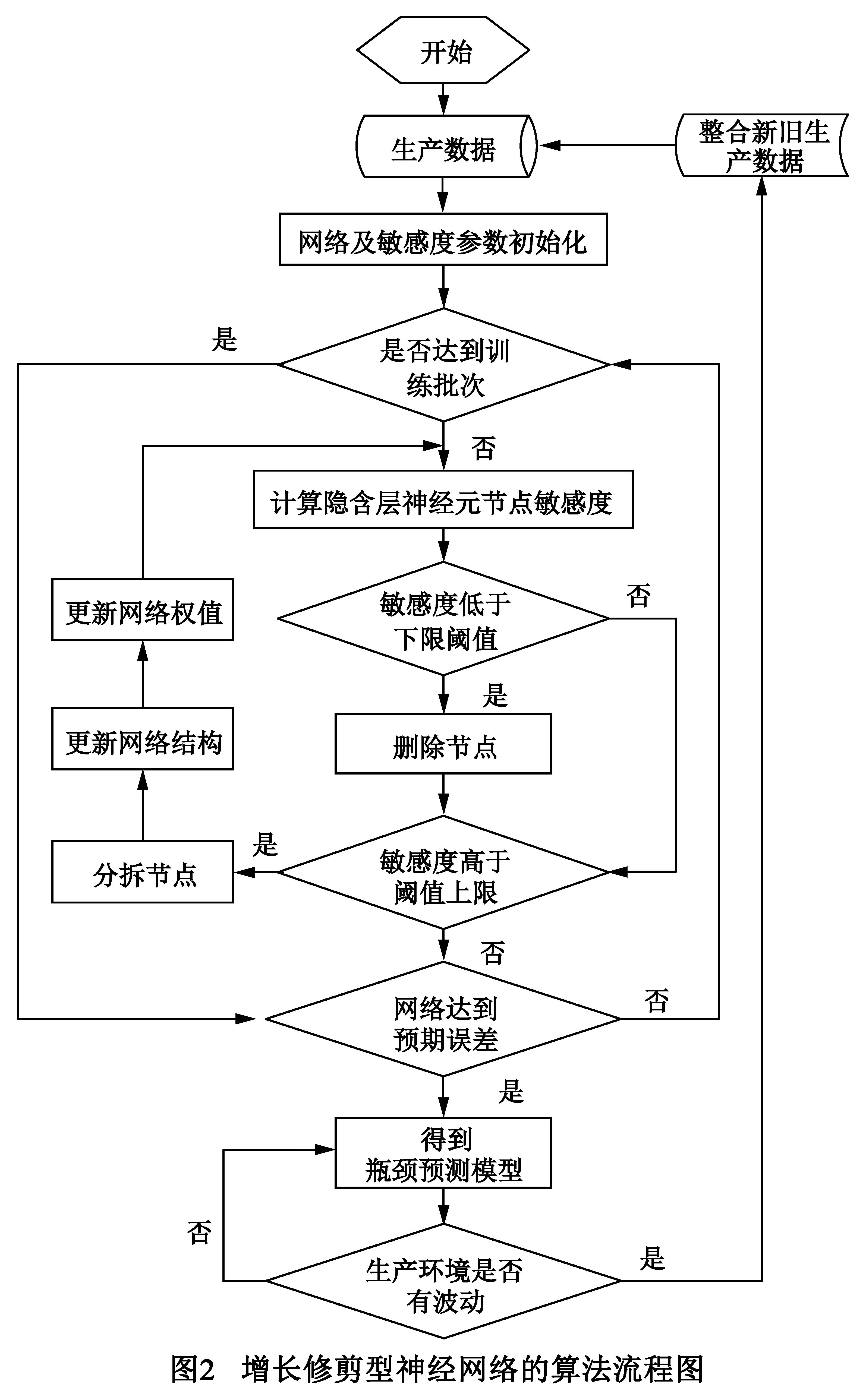
(1)通过LM算法对上述建立的模型进行训练，直至达到要求时停止训练；

(2)训练的过程中，隐含层神经元j对应的输出层神经元k的输入为wkjOj，对wkjOj进行傅立叶变换，即：

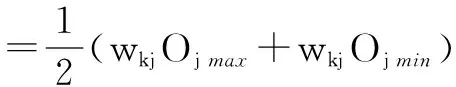
(11)

其中，ωj为变换选定的频率，wkjOj max、wkjOj min分别为神经元j输出的最大值和最小值.模型输出为：

ym(t)=f(wkjOj(t))

(12)

同时，模型输出则可转变为：

y(s)=ym(s)=F(wkjOj(s))

(13)

其中，Aj、Bj为傅立叶系数.

(3)隐含层神经元j对应的输出层神经元k的输入为wkjOj，此神经元节点对模型输出的贡献可约简为输出的一阶灵敏度，即：

(14)

其中，varj[E(y|wkjOj)]为隐含层神经元节点j对模型输出的影响，var(ym)为输出ym的方差.根据式(13)，输出ym的方差为：

(15)

由于模型的隐含层神经元输出间无相互耦合关系，傅立叶振幅主要分布在基频(K=1)上，则隐含层神经元节点j的敏感度：

(16)

将隐含层神经元节点j的敏感度归一化：

(17)

(4)设定模型隐含层神经元的敏感度范围[α,β](0<α<β<1)，将敏感度低于α的隐含层神经元删除；将敏感度超过β的神经元分解为d个；保留敏感度在[α,β]范围内的神经元.对分解后得到的新神经元的连接权值、阈值进行初始值；

(5)当训练次数达到N次则重复步骤(1)至(4)，直至隐含层神经元的敏感度都在设定范围内，至此隐含层神经元的数目则不再发生变化；

(6)继续利用LM算法对模型进行训练，直至训练误差e低于模型期望误差ed，则模型构建过程结束.

由此将设备故障间隔时间和平均修复时间、缓冲区队列长度、设备平均加工时间、设备利用率、设备加工时间及生产线在制品水平(WIP)等生产线关键参数作为以上预测模型的输入；将已识别出的相应瓶颈设备作为预测模型输出.故实际SWFS瓶颈预测模型可如下：

y=f(x1,x2,x3…,x7×(i-1)+j,…x7×23+7)

(18)

其中，x7(i-1)+j：i=1,2,…代表生产线上设备群编号；j=1,2…分别代表生产线关键参数：设备故障间隔时间、平均修复时间、缓冲区队列长度、设备平均加工时间、设备利用率、设备加工时间、WIP；y为生产线下一时刻的瓶颈设备编号.

3.2基于闭环控制思想动态修正模型

当模型受到不确定因素影响时，瓶颈设备漂移现象严重，预测结果与实际情况偏差较大，这时需要对模型结构重新修正以适应新的生产环境；而在相对较短时间内，生产线是相对稳定，瓶颈设备变化不大，则不需实时预测，可将上一时刻的预测结果直接作为下一时刻瓶颈，直至出现偏差为止，可使模型效果预测更加高效.如图1所示：

(1)将从生产线所获得的t时刻数据，输入到所建立的模型，预测t+1时刻瓶颈；

(2)单位采样时间后，利用式(7)并结合瓶颈判定机制获取t+1时刻的实际瓶颈，将其与t时刻预测得到的瓶颈相比较，判断是否一致，若不一致，则将修正信息反馈到模型构建阶段，并整合新旧生产数据再次对模型进行训练，以达到生产要求；如果一致，则认为所建立的预测模型仍是有效，并可将t+1时刻瓶颈直接作为t+2时刻的预测结果，而不需使用模型；

(3)若t+2时刻实际得到的瓶颈与预测得到一致，则可依次直接得出下一时刻瓶颈；若实际t+2时刻得到的瓶颈与预测不符，则需要使用预测模型，转入步骤(1)；若由预测模型得到结果都不能满足要求，则转入模型构建阶段重新训练网络以适应新环境.

在实际生产线中，基于瓶颈设备漂移的预测机制有利于生产线快速有效的预测瓶颈，并且能够保证生产线的稳定性.

4　基于单因子试验法的瓶颈分析

上述部分完成对SWFS瓶颈设备识别、预测及模型动态修正，继而可以利用单因子试验法分析相关参数变化对瓶颈的影响.利用单因子试验法分析瓶颈，仅考查单个参数波动对生产线瓶颈的影响.但在实际生产线中，各种参数并不是相互独立，而是存在着耦合关系.为实现利用单因子试验法分析瓶颈，可采用统计学知识对各种历史数据进行分析，确定各种参数之间定量的耦合关系，以得到生产线参数对瓶颈漂移的独立影响.

在单位时间T内，k类生产线上参数s1,s2,…,sk发生变化的概率为p(si)，则概率模型可表示如式(19)所示：

P(Ω)={p(s1),p(s2),…,p(sk)}

(19)

其中，Ω：各种参数集合：

Ω={s|s1,s2,…,sk}

(20)

参数si在参数sj的影响下发生波动的概率为：

(21)

通过以上多个参数间连带关系，将参数si引起sj波动而导致sj对设备m的影响折算到si，如式(22)所示：

(22)

5　实验结果

采用文献[12]中的SWFS模型验证文中提出的瓶颈设备分析方法的有效性.该生产线模型拥有24个设备群，共78台设备，其中批加工设备6台，单件加工设备72台，并且设备存在混合加工和重入的现象，可加工A、B、C三种类型工件.

在eM-Plant仿真平台上构建该生产模型，采用固定投料策略和基于生产线平衡的FLNQ(Longest Lots at the Next Queue)派工规则进行仿真实验，仿真时间为三年，预仿真时间半年.采集生产线数，每个采样点依据建立的实际预测模型可包括7项输入、1项输出，共八项数据，并对数据做预处理：①剔除半导体制造系统预仿真时间段内及设备生产能力未达到饱和状态时的数据；②剔除超出三倍数据样本标准差的数据.将处理后的数据作为构建GPNN模型所需的数据.

初始化GPNN模型相关参数：将模型隐含层节点设置为15，神经元敏感度范围设置为[5%,50%]，神经元分裂数目d为4.利用所获数据对初始化后的模型进行训练和测试，如图3中，基于GPNN模型隐含层节点从初始15个节点最终收敛到7个，根据经验公式(9)计算得到节点数范围[3,13]内，其结构更加趋于合理简洁.由于GPNN模型动态优化网络结构，获得更优隐含层节点数，使得模型收敛速度更快，并且能达到较高精度如.如图4，GPNN预测模型训练和测试的均方差分别降至5.82×10-2、6.32×10-2，满足SWFS的实际要求.

在半导体生产线中，稳定的生产环境对瓶颈设备的影响不大，生产线瓶颈设备分布趋势如图5所示.利用单因子试验法对瓶颈进行分析，观察生产线参数变化对瓶颈设备的影响.根据生产线实际生产经验，可主要通过改变最能直接体现生产线设备拥挤程度的关键参数，如生产线WIP水平和设备缓冲区队列长度等，得到生产线稳定时的合理参数范围.

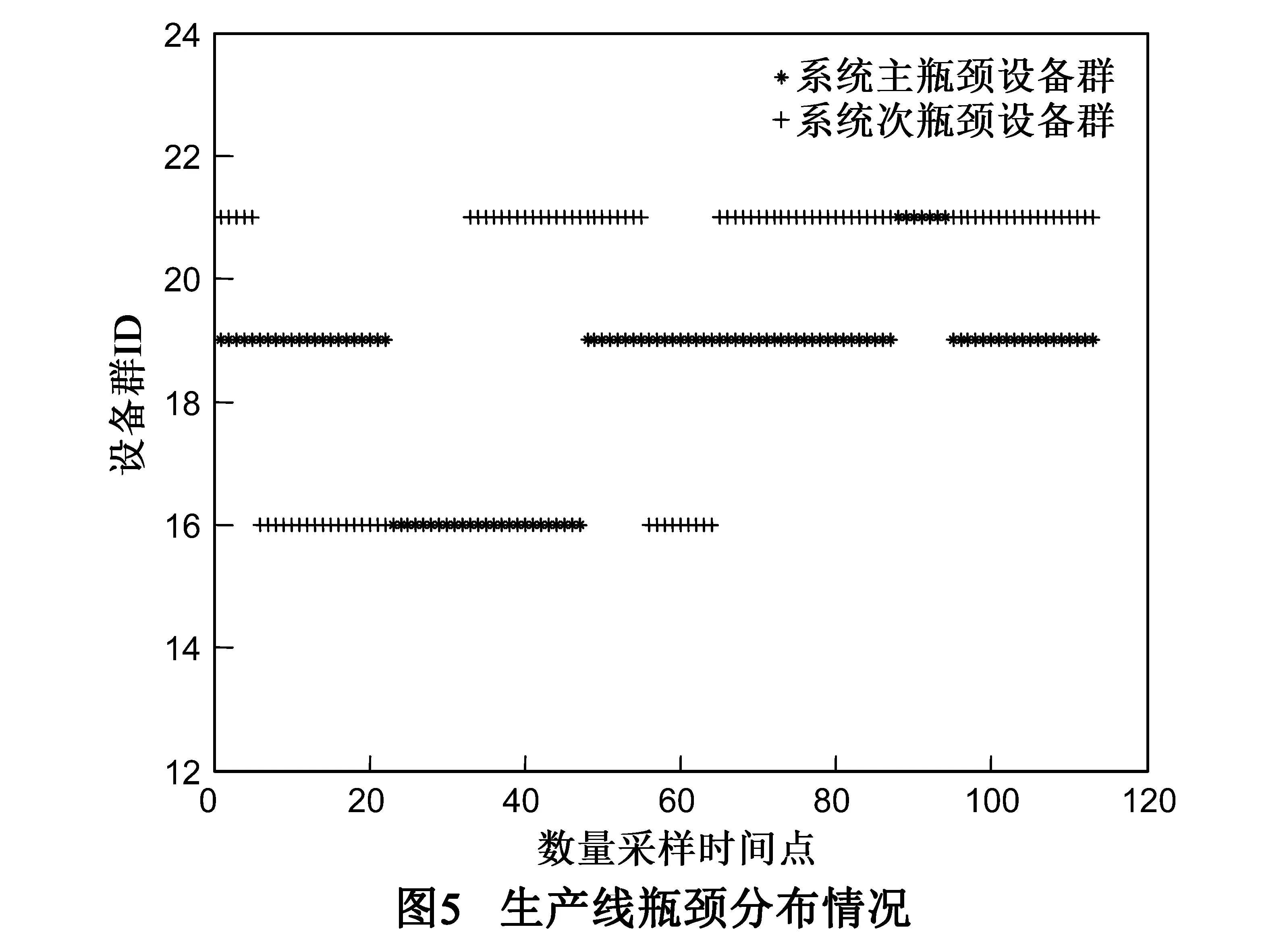
(1)改变生产线WIP值

当生产线WIP水平设置为[25,35]lot时，对瓶颈设备影响较小；当WIP水平超过上界并达到40lot时，如图6所示，主瓶颈设备在第23至47采样时刻及第86至95采样时刻发生漂移，由原来19号设备向16号、21号设备转移，最后又回归到19号设备.次瓶颈设备则依次在16、19和21号设备间转移，第23至34采样时刻生产线只有唯一19号瓶颈设备.因此，通过提高生产线WIP水平，对主瓶颈设备无较大影响，而对次瓶颈前的设备瓶颈度影响很大，容易引起生产线次瓶颈设备的前移.

(2)改变设备缓冲区容量

当缓冲区容量由无限容量调整到30个工件，如图7所示，主瓶颈基本都维持在19号设备，只在第20至40采样时刻及第65至72采样时刻主瓶颈发生漂移，此时16和21号设备成为生产线瞬时主瓶颈；次瓶颈则主要由原来16号转移到18号设备，由于缓冲区容量设置使得18号设备加工完的工件无法及时传送给19号设备，导致18号设备缓冲区前积累大量未加工工件，使得18号设备成为次瓶颈.因此，通过对减小设备缓冲区容量设置，生产线上主瓶颈上游设备发生了工件积压的现象，导致无法正常生产，增加其成为次瓶颈的概率.

6　结论

本文针对在不确定环境下半导体生产线动态瓶颈的识别与预测问题进行研究，给出一种基于增长修剪型神经网络的动态瓶颈分析方法.利用复合定义法进行瓶颈识别，构建基于增长修剪型神经网络的瓶颈预测模型，同时使用单因子试验法得到生产线稳定时参数对应的合理范围.实验表明，该方法能够快速有效的识别并预测下一时刻的瓶颈，并能描述关键参数对生产线的影响，极大地改善不确定性环境下动态瓶颈漂移所带来的调度算法缺乏柔性的问题，具有一定工程实践意义.

[1]Qiao F,Ma Y M,Li L,et al.A Petri net and extended genetic algorithm combined scheduling method for wafer fabrication[J].IEEE Transactions on Automation Science and Engineering,2013,10(1):197-204.

[2]Cao Z C,Peng Y Z,et al.A drum-buffer-rope based scheduling method for semiconductor manufacturing system[A].IEEE Conference on Automation Science and Engineering[C],2011.120-125.

[3]Meidan Y,Lerner B,Rabinowitz G,et al.Cycle-time key factor identification and prediction in semiconductor manufacturing using machine learning and data mining[J].IEEE Transactions on Semiconductor Manufacturing,2011,24(2):237-248.

[4]Zhou Z,Rose O.A bottleneck detection and dynamic dispatching strategy for semiconductor wafer fabrication facilities[A].Winter Simulation Conference[C],2009.1646-1656.

[5]乔非，马玉敏，李莉，等.基于分层瓶颈分析的多重入制造系统调度方法[J].计算机集成制造系统，2010，16(4)：855-860.

Qiao F,Ma Y M,Li L,et al.Multi-reentrant manufacturing system scheduling based on layered bottleneck analysis[J].Computer Integrated Manufacturing Systems,2010,16(4):855-860.(in Chinese)

[6]Wang,Z J,Chen J,Wu Q D,A new method of dynamic bottleneck detection for semiconductor manufacturing line[A].Proceedings of the 17th World Congress the International Federation of Automatic Control[C],2008,17(1):14840-14845.

[7]Li L,Chang Q,Ni J.Data driven bottleneck detection of manufacturing systems[J].International Journal of Production Research,2009,47(18):5019-5036.

[8]Cao Z C,Deng J J,LIU M,et al.Bottleneck prediction method based on improved adaptive network-based fuzzy inference system in semiconductor manufacturing system[J].Chinese Journal of Chemical Engineering,2012,20(6):1081-1088.

[9]Moss H K.Toward the estimation of bottleneck shiftiness in a manufacturing operation[J].Production and Inventory Management Journal,1999,40:53-58.

[10]Liu M Z,Tang J,Gen M G,et al.Dynamic prediction method of production logistics bottleneck based on bottleneck index[J].EI on Chinese Journal of Mechanical Engineering,2009,22(5).

[11]夏克文,李昌彪,沈钧毅.前向神经网络隐含层节点数的一种优化算法[J].计算机科学,2006,32(10):143-145.

Xia K W,Li C B,Shen J Y.An optimization algorithm on the number of hidden layer nodes in feed-forward neural network[J].Computer Science,2006,32(10):143-145.(in Chinese)

[12]Chen J H,Fu L C,Lin M H,et al.Petri-net and GA-based approach to modeling,scheduling,and performance evaluation for wafer fabrication[J].IEEE Transactions on Robotics and Automation,2001,17(5):619-636.

曹政才男，博士，教授/博导，主要研究方向：复杂生产过程优化调度,系统工程和智能控制.

E-mail:giftczc@163.com

邱明辉男，硕士，主要研究方向为复杂过程建模、优化与控制等.

E-mail:2013210279@grad.buct.edu.cn

刘民男，博士，教授/博导，主要研究方向为复杂生产过程优化调度，复杂生产过程或装备智能检测和智能操作优化，智能优化方法及其在复杂制造系统建模、调度与优化中的应用.

E-mail：lium@tsinghua.edu.cn

Dynamic Bottleneck Analysis for Semiconductor Wafer Fabrication System Based on Growing and Pruning Neural Networks

CAO Zheng-cai1,2,QIU Ming-hui1,2,LIU Min3

(1.College of Information Science and Technology,Beijing University of Chemical Technology,Beijing 100029，China; 2.Key Laboratory of Symbolic Computation and Knowledge Engineering of Ministry of Education,Jilin University,Changchun，Jilin 130012，China; 3.Department of Automation,Tsinghua University,Beijing 100084，China)

Bottleneck is the key factor to semiconductor wafer fabrication system (SWFS),which seriously influences the level of work-in-process,cycle time,time-delivery rate,etc.Efficient analysis for the bottleneck of SWFS can promote various performances.In modern SWFS,present analysis methods usually regard bottleneck device as static bottleneck without taking bottleneck shifting into consideration in the uncertain environment,which leads to scheduling algorithm that always treat the bottleneck device as the core lack of flexibility and real-time performance.Therefore,dynamic bottleneck analysis method for the SWFS based on growing and pruning neural networks (GPNN) was adopted in this study to acquire the dynamic bottleneck characteristic.Firstly,in this paper,the way of composite definition is used to calculate comprehensive bottleneck degree of the devices form the perspectives of relative production load,utilization rate and length of the buffer queue to indicate bottleneck based on bottleneck identification mechanism;Secondly,establish the model of growing and pruning neural networks to predict the future bottleneck and adjust the network structure in view of closed-loop control.Thirdly,in order to analyze the key factors relative to bottleneck devices and the dynamic bottleneck characteristic quantitatively,the single factor test method was applied in this paper.Lastly,the experiments show that this dynamic bottleneck analysis method is testified the feasibility and availability.

SWFS；dynamic bottleneck analysis；comprehensive bottleneck degree；GPNN；single factor test method

2014-02-27;

2014-07-07;责任编辑：郭游

国家自然科学基金(No.51375038);高等学校博士学科点专项科研基金博导类课题(No.20130010110009);复杂系统管理与控制国家重点实验室开放课题(No.20120104);吉林大学符号计算与知识工程教育部重点实验室开放课题

TP373

A

0372-2112 (2016)07-1636-07

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.07.017