墙体参数未知时的穿墙雷达实时成像方法

张华美，张业荣，王芳芳

(南京邮电大学电子科学与工程学院,江苏南京 210003)

墙体参数未知时的穿墙雷达实时成像方法

张华美，张业荣，王芳芳

(南京邮电大学电子科学与工程学院,江苏南京 210003)

为同时解决穿墙雷达成像中墙体参数未知和实时性要求这两个关键问题，提出了先利用支持向量机对墙体参数进行回归预测、再采用相移偏移算法进行成像的两步成像方法.重点介绍了墙体参数预测方法，讨论了目标的大小、位置、形状和个数及墙体长度、采样间隔、噪声对墙体参数预测的影响，仿真结果表明预测方法精度高、耗时短.对实际案例进行仿真分析，结果表明该两步方法成功地实现了墙体参数未知时的实时成像，成像结果令人满意.

穿墙成像；参数估计；实时性；支持向量机

1　引言

穿墙雷达和探地雷达、医学成像、地球物理观测等同属于无损检测，能根据有限的信息推断非视距范围内的目标信息.不管军事上还是民用上，穿墙雷达都有着广泛的应用，受到了极大的关注.

穿墙雷达既要求成像质量高，又要求实时性，而墙体的存在使这两个要求很难同时满足.若墙参(介电常数、电导率、墙体厚度)已知，很多成像算法(例如后向投影算法等)中容易纠正由墙体引起的偏移效应.但在实际情况中，墙参是未知的.因此，如何解决墙参未知时的实时成像，是目前穿墙问题面临的难题.

介于墙参的未知性和重要性，近几年，很多研究致力于墙参估计[1].研究方法主要分成两类.第一类，轨迹交点法.通过放置不同的天线阵、或者把天线阵放置在离墙不同的位置，形成不同的曲线，曲线的交点即是准确的墙参[2,3].此类方法正确性高，不足是至少需要两次实验.第二类，价值函数法[4,5].把某计算指标和墙参的测量值构造成一价值函数，最小化价值函数即得到墙参.这类方法得到的估计值和真实值很接近，不足是计算时间长.另外，Jin Tian等[6]根据等效传输线模型提出了基于滤波的估计方法，即移除墙体的影响构造滤波器，于是墙参的估计就转换成在获得目标高质量图像基础上得到滤波器的最优化参数.该方法估计精度高、速度快，但没有涉及对电导率的估计.Protiva Pavel等[7]提出了时延估计方法，该方法通过收发天线间隔不同时产生的不同时延来估计墙参，只需几秒的时间，但至少需要两次试验.

随着智能算法在无损检测领域的广泛应用，支持向量机(Support Vector Machine，SVM)被用于穿墙问题[8,9].SVM基于结构风险最小原则，建立在统计学习的Vapnik-Chervonenkis维理论基础上，通过求解一个凸二次规划问题，得到全局最优解，具有良好的泛化性和实时性.穿墙问题中已实现了SVM对目标中心位置[8]和电磁参数[9]的重构，但只适用于单目标情形，且未见SVM用于墙参估计的报道.

在墙参已知的情况下，相移偏移(Phase Shift Migaration，PSM)算法[10]采用快速傅里叶变换技术，能实时对目标进行成像.PSM算法是基于波动方程的频域算法，最初用于地理探测、地震信号的处理，适用于媒质呈层状分布的区域[11].在多数穿墙问题中，可近似认为电磁波沿水平层状媒质传播，因此PSM算法适用于穿墙问题[12].

本文描述了穿墙成像问题，提出了利用SVM进行墙参估计的方法，再根据估计的墙参进行PSM成像.由于SVM是“单输出”的学习方法，故需要分别建立墙体各参数的SVM模型.对于建模时目标不变的情况，讨论了目标的大小、位置、形状和个数变化时墙参的预测值和真实值之间的关系.为了验证SVM方法在实际中的应用能力，讨论了墙体长度、天线的采样间隔和噪声对预测结果的影响.最后，对墙参未知的实际案例进行仿真分析，分别根据墙参预测值和真实值进行成像，比较了两者的成像结果.

2　算法原理与实现

2.1问题描述

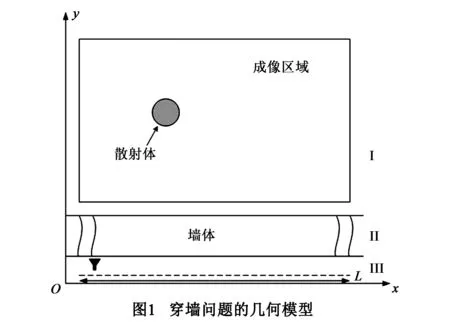
穿墙问题的几何模型如图1所示，假设墙体是单层、均匀的媒质，其厚度、相对介电常数和电导率分别为dw、εw和σw.成像区域在墙体的一侧，其中放置一个目标.一天线放置在墙体的另一侧，平行于墙体直线移动，形成长度为L的合成孔径，L等于墙体长度.天线采样位置等间隔，逐个在采样位置发射并接收信号(收发共置的方式).本文用时域有限差分(Finite Difference Time Domain，FDTD)法仿真，模拟发射信号为调制高斯脉冲信号，中心频率为2GHz，脉冲带宽为1.2ns.接收信号存储后用于目标的探测和定位.

接收信号中包含直射波、墙面反射波与折射波、目标散射波等信号，目标探测时只需其散射信号.该信号可通过背景相减法获得，即在相同的几何模型下，用有目标时的接收信号减去无目标时的接收信号，可得目标的散射信号.

由于墙体的存在，目标的散射信号和成像信息不是线性关系，加诸墙参未知，要快速对目标进行成像，一种方法是先估计墙参，然后再成像.本文将从散射信号中提取的信号作为输入，墙参作为输出，通过SVM训练得到两者关系的近似表达式.再根据估计的墙参，利用PSM算法成像.

2.2基于SVM的墙体参数估计方法

SVM主要特点是利用核函数把低维空间的非线性关系变换为高维空间的线性关系，以便找出输入信号和输出信号之间的线性表达式.

设给定的训练集为T={(x1,y1),…,(xl,yl)}，其中xi∈R2n为输入信号，yi∈R为输出信号，i=1,…,l，l为训练样本数.在墙参估计方法中，x是一维向量，由等距采样位置提取的目标散射信号的最大振幅值(x的前n元)和最大振幅对应的时间(x的后n元)组成；y是一个实数，表示墙参.

设线性回归函数为：

y=(w·x)+b

(1)

其中，(·)为内积运算符号，w和b分别为权重向量和偏置.

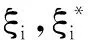
(2)

s.t.((w·xi)+b)-yi≤ε+ξi,

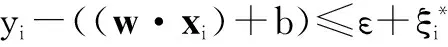
ξi≥0,

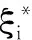
(3)

式中C为惩罚因子，是泛化能力和拟合误差的一个折衷.利用拉格朗日方法求解上述约束最优化问题，将原问题转化为其对偶问题，即为：

(4)

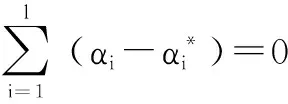
(5)

(6)

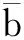
对于新的x，可通过式(6)计算得到相应的y.

2.3PSM算法

PSM算法由Gazdag在1978年提出[10]，基本思路是：在频率波数域实现波场延拓，再利用傅里叶逆变换得到每一深度t=0时刻的波场，从而可将测量到的波场延拓到任意深度.

假设接收天线的横坐标为x，纵坐标为z0，散射信号为e(x,z0,t)，二维PSM算法的计算步骤如下：

(1)输入e(x,z0,t)，分别对x,t进行Fourier变换，得到E(kx,z0,ω)，

E(kx,z0,ω)=∫∫e(x,z0,t)exp(-jkxx)exp(-jωt)dxdt

(7)

(2)在频率-波数域进行波场外拓，延拓步长为Δz.如果取Δz小于每层媒质的厚度，则在Δz内纵向速度不变.雷达是收发共置的工作方式，从发射天线到反射点和从反射点到接收天线的路程是重叠的，电磁波总传播时间是从反射点到接收天线传播时间的2倍，因此可以把波速看作波在传播媒质中实际传播速度的一半，外推z1=z0+Δz的波场表示式为：

(8)

(3)对式(8)在kx,ω域进行逆Fourier变换，并令t=0，得到：

(9)

e(x,z1,t=0)是深度z=z1处的相移偏移结果.

(4)在每一深度zm+1=zm+Δz,m=0,1,…,M-1.重复步骤(2)、(3)，即可得到整个成像区域的波场分布.

3　基于SVM的墙体参数预测方法

墙体模型如图1所示，墙体的介电常数和厚度未知，长2.4m.天线沿x轴移动，采样间隔0.02m，形成L=2.4m的合成孔径.墙后放置一中心位置为(1.2m，1.3m)、半径ρ=0.15m的圆形目标.

3.1建立SVM模型

穿墙问题中，墙体材料为混凝土、砖、石灰石等，一般这些材料的εw∈[3,7]，dw∈[0.1m,0.3m].墙参未知时，设σw=0，而εw、dw按以下方式改变：

(10)

式中，Δε=0.25、Δd=0.01m分别是相对介电常数、厚度的采样间隔.每一组εw和dw对应一对墙参，这样得到了357个样本.选取其中的178个样本作为训练样本，其x是训练数据.其他的作为测试样本，其x是测试数据.利用SVM对εw和dw分别训练，并采用径向基(Radial Basis Function，RBF)核函数，从而得到两个回归模型modelper和modelthick.用其对测试样本进行预测，结果见图2.

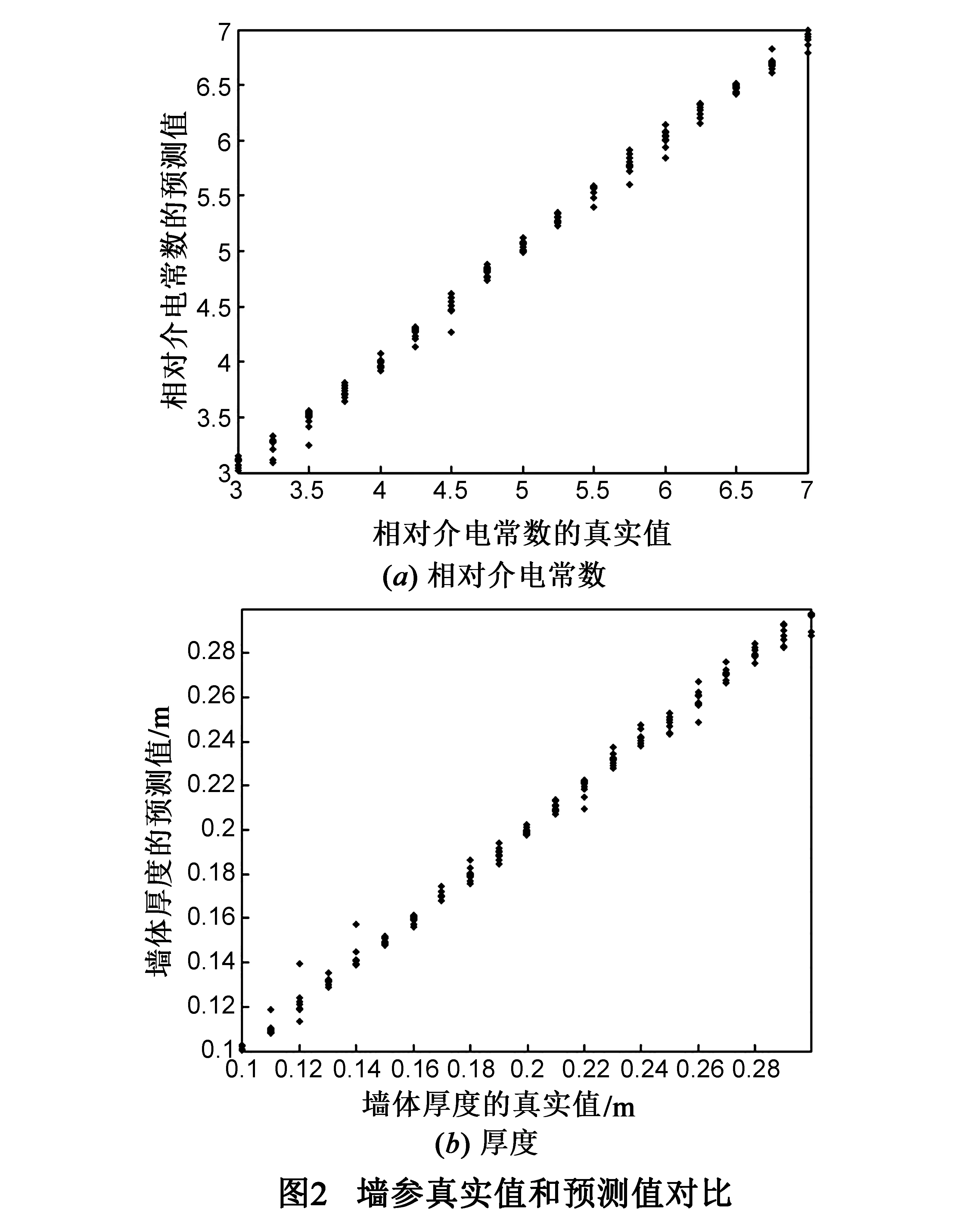
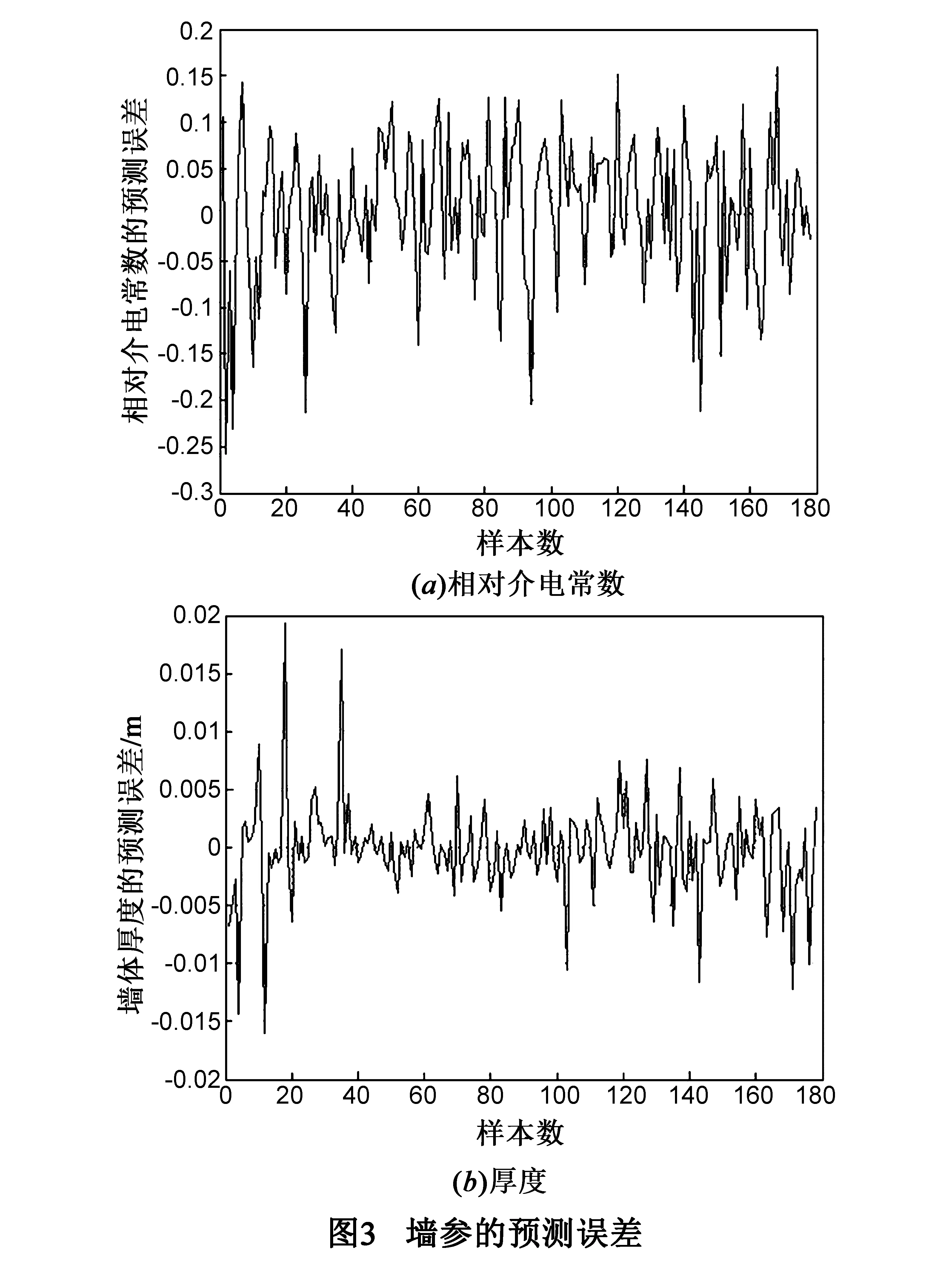
图2显示了墙参的预测值和真实值非常接近，图3定量地给出了误差结果，εw和dw的预测误差分别控制在0.1和0.005m之内.从图3(b)可知预测dw时，墙体厚度比较薄时误差稍大.

SVM训练中采用RBF核函数时，调节C和核函数系数σ2，得到平方相关系数(Squared Correlation Coefficient，SCC)以判断预测值和真实值的拟合程度.SCC越接近1，表示拟合效果越好.本文采用网格寻优的方式寻找最佳值.建立modelper和modelthick时，C的最佳值分别为Cp=194.0和Ct=97.0，SCC为0.996和0.995.若保持σ2的最佳值不变，Cp=Ct=700，SCC保持不变；Cp=Ct=1，SCC为0.988和0.821.因此，σ2不变时，仅调节C，模型的拟合程度基本不变，对预测结果没有影响.

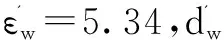
3.2外界因素对墙体参数预测的影响

设墙参为εw=5.28，dw=0.2m，利用modelper和modelthick分别对εw和dw进行预测.

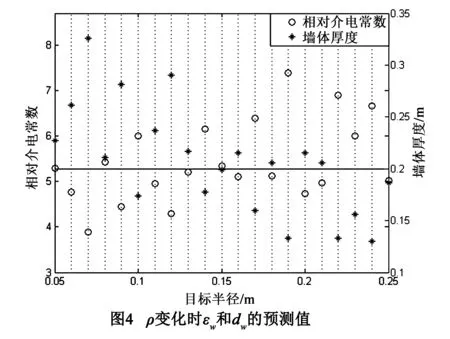
若目标位置不变、ρ从0.05m递增到0.25m，递增间隔为0.01m，预测结果见图4.在图4中，横实线代表εw和dw的真实值；εw和dw随半径的变化无固定规律，但半径相同时，εw和dw中必定一个大于真实值，另一个小于真实值，两者的误差在成像算法中恰可相互抵消[6].

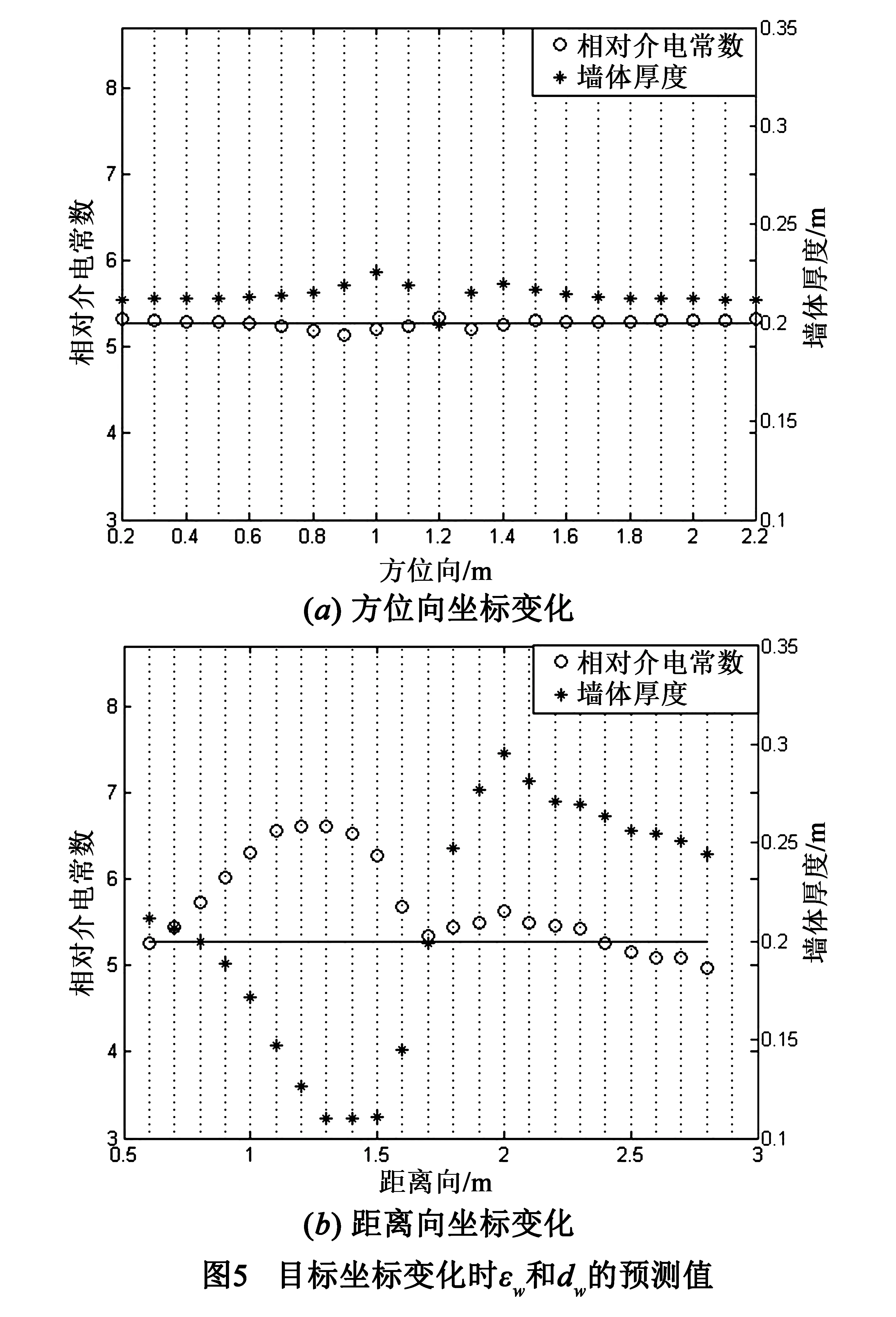
若ρ=0.15m不变，目标方位向坐标从0.2m递增到2.2m，距离向坐标从0.6m递增到2.8m，递增间隔都为0.1m，预测结果见图5.图5(a)中显示εw和dw的预测值都较稳定，εw的预测值和真实值基本一致，且不受方位向坐标变化的影响.dw的预测值几乎都比真实值大，但误差都在0.013m内，对实际成像影响不大.从图5(b)看出，εw和dw随距离向坐标变化时起伏较大，但基本保持一个大于真实值、一个小于真实值的规律.两值同时大于或者小于真实值则为存在一定的误差，但属于少数情形.

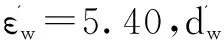
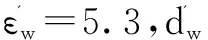
若目标半径、形状不变，中心位置的纵坐标不变、横坐标同墙体的中心位置坐标，墙体长度从0.08m递增到0.48m，递增间隔为0.02m，合成孔径长度同墙体长度.则预测结果和多目标时的一样.

若天线间的采样间隔从0.02m递增到0.4m，递增间隔为0.02m，合成孔径长度保持基本不变，其余参数不变.则预测结果同多目标时的结果.

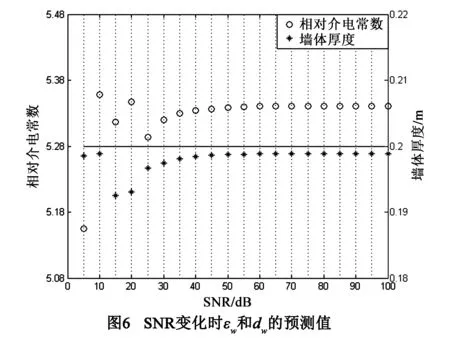
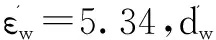
以上分析表明，当测试数据由于目标状态、墙体长度、采样间隔发生改变或被噪声污染而出现一定的失真时，预测的墙参也能为成像算法提供可靠、有效的数据.SVM方法的预测精度受目标大小、位置和形状变化的影响相对较大，但几乎不受目标个数、墙体长度、采样间隔和噪声的影响，体现了SVM方法的鲁棒性和良好的泛化性.但在穿墙问题的几何模型中，获得测试数据时天线的收发方式、离墙的距离必须和获得训练数据时相同，否则测试数据的输入和输出信号之间的关系和已建模型不存在联系，导致预测结果无效.穿墙雷达天线在墙外布置，容易做到和建模时一样，因而本文提出的方法具有实用性.

4　墙体参数未知时的实时成像

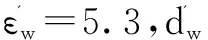
从图7看出，根据两种墙参都能得到定位精确、无散焦的高质量图像.且当modelper和modelthick已知时，在Inter Core 2.6GHz 4CPUs的计算机上，预测墙参只需不足一秒的时间，远远小于价值函数法的预测时间；利用PSM算法成像时，也只需二十几秒的时间.两者相加不超过三十秒，满足实时要求.且SVM预测方法只需一次试验即可，相比轨迹交点法，更易在实际中应用.

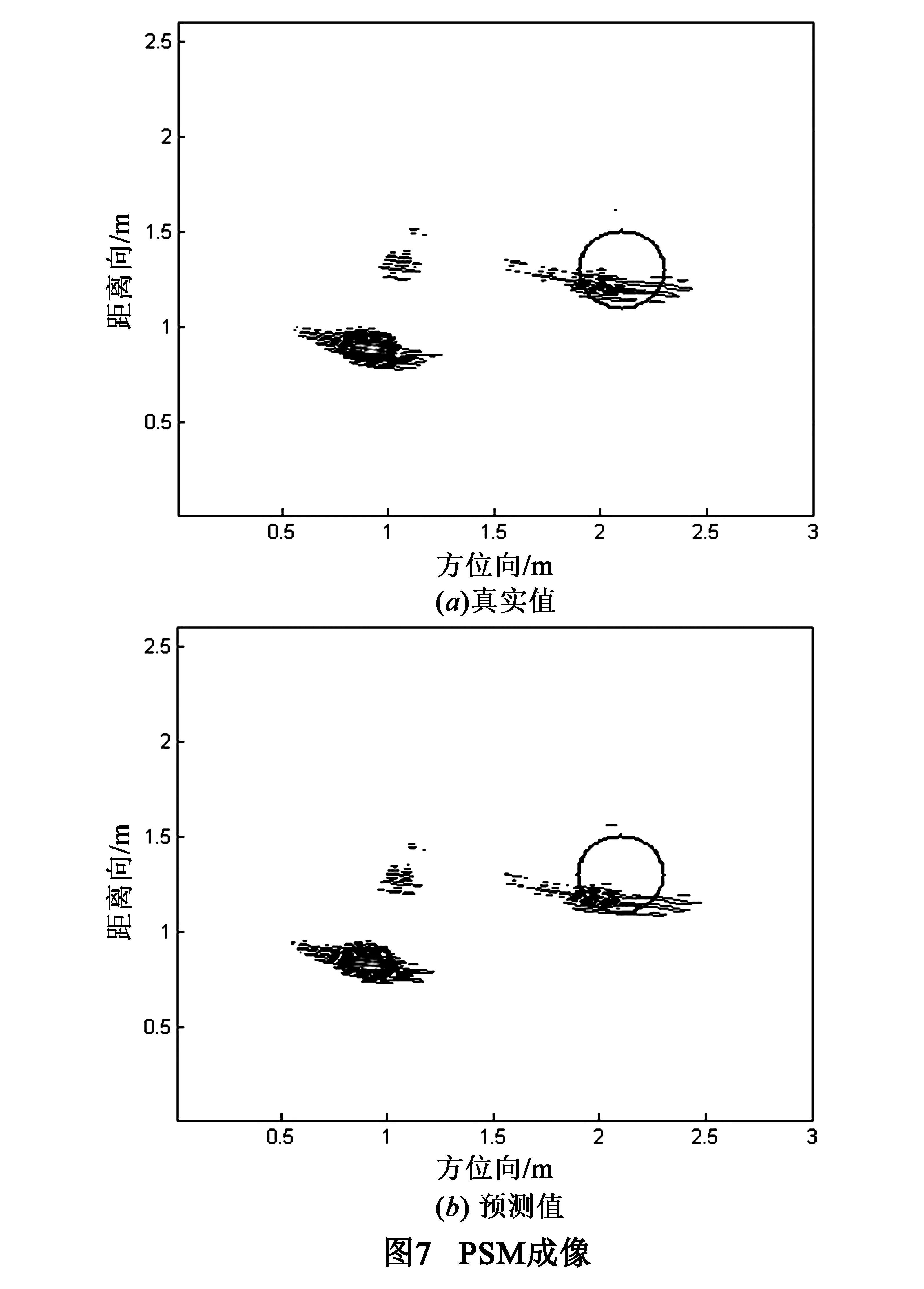
5　结论

鉴于穿墙雷达中的墙参未知和实时性问题，本文提出了一种两步成像的方法.该方法首先利用SVM对墙参进行快速、有效地回归估计，再利用PSM算法进行成像，实现了穿墙雷达问题中墙体参数未知时的实时成像.实际案例的高质量成像有力地证实了本文方法的可行性和鲁棒性.利用SVM进行墙参预测时，预测精度受目标大小、位置和形状变化的影响相对较大，但几乎不受目标个数、墙体长度、采样间隔和噪声的影响；只需一次实验即可；能实时估计出墙参；估计值能为成像算法提供有效的数据；另外，若建立模型时包含了电导率的信息，SVM还能预测墙体的电导率；但SVM只能胜任单层墙体的墙参预测，无法处理多层墙体的情况，因此下一步的研究工作包括如何实现多层墙体时的墙参未知时的实时成像.

[1]金添,孙鑫,李欣,等.SAR穿墙成像中墙体影响图像域补偿方法[J].电子学报,2012,40(7):1424-1428.

Jin Tian,Sun Xin,Li Xin,et al.A method to compensate wall effects in the image domain for SAR through-the-wall imaging[J].Acta Electronica Sinica,2012,40(7),1424-1428.(in Chinese)

[2]Wang Gen-yuan,Amin M G.Imaging through unknown walls using different standoff distances[J].IEEE Transactions on Signal Processing,2006,54(10):4015-4025.

[3]Wang Gen-yuan,Amin M G,Zhang Yi-min.New approach for target locations in the presence of wall ambiguities[J].IEEE Transactions on Aerospace and Electronic Systems,2006,42(1):301-315.

[4]Dehmollaian M,Sarabandi K.Refocusing through building walls using synthetic aperture radar[J].IEEE Transactions on Geoscience and Remote Sensing,2008,46(6):1589-1599.

[5]Solimene R,Soldovieri F,Prisco G,et al.Three-dimensional through-wall imaging under ambiguous wall parameters[J].IEEE Transactions on Geoscience and Remote Sensing,2009,47(5):1310-1317.

[6]Jin Tian,Chen Bo,Zhou Zhi-min.Imaging-domain estimation of wall parameters for autofocusing of through-the-wall SAR imagery[J].IEEE Transactions on Geoscience and Remote Sensing,2013,51(3):1836-1843.

[7]Protiva P,Mrkvica J,Machac J,et al.Estimation of wall parameters from time-delay-only through-wall radar measurements[J].IEEE Transactions on Antennas and Propagation,2011,59(11):4268-4278.

[8]王芳芳,张业荣.基于支持向量机的电磁逆散射方法[J].物理学报,2012,61(8):084101-084208.

Wang Fang-fang,Zhang Ye-rong.An electromagnetic inverse scattering approach based on support vector machine[J].Acta Physica Sinica,2012,61(8):084101-084208.(in Chinese)

[9]Wang Fang-fang,Zhang Ye-rong.The support vector machine for dielectric target detection through a wall[J].Progress in Electromagnetics Research Letters,2011,23:119-128

[10]Gazdag J.Wave equation migration with the phase-shift method[J].Geophysics,1978,43(7):1342-1351.

[11]Olofsson T.Phase shift migration for imaging layered objects and objects immersed in water[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,2010,57(11):2522-2530

[12]Gu Xiang,Zhang Yun-hua.Autofocus imaging simulation for through-wall radar by using FDTD with unknown wall characteristics[A].Proceeding of Asia-Pacific Microwave Confeerence[C].Yokohama:IEEE,2010.1657-1660.

张华美女,1979年10月出生于江苏启东.现为南京邮电大学电子科学与工程学院讲师.主要研究方向为电磁场的数值计算、电磁逆散射及成像等.

E-mail:zhanghm@njupt.edu.cn

张业荣(通信作者)男,1963年4月出生于安徽和县.现为南京邮电大学电子科学与工程学院副院长，教授、博士生导师.主要研究方向为电磁散射与成像、电波传播、无线通信的信道建模等.

E-mail:zhangyr@njupt.edu.cn

王芳芳女,1985年2月出生于江苏丹阳.现为南京邮电大学电子科学与工程学院讲师.主要研究方向为电磁散射与逆散射、电磁成像算法等.

E-mail:wangff@njupt.edu.cn

A Real-Time Approach for Through-the-Wall Imaging Under Unknown Wall Characteristics

ZHANG Hua-mei,ZHANG Ye-rong,WANG Fang-fang

(School of Electronic Science and Engineering,Nanjing University of Posts and Telecommunications,Nanjing,Jiangsu 210003,China)

In order to solve two key problems in through-the-wall imaging which are ambiguities of wall parameters and real-time imaging simultaneously,a two step imaging procedure is presented in which firstly the wall parameters are estimated by support vector machine and then the targets behind the wall is located and focused by phase shift migration algorithm.The estimated method is introduced emphatically,and the influence of the size,the location,the shape,the number of the targets and the length of the wall,sampling interval,noise on the estimated wall parameters is mainly discussed.The results demonstrate that the method based on SVM(Support Vector Machine) has the advantages of high precision and low computational time.Finally,the performance of two step imaging procedure is tested by a practical case of through-the-wall imaging,the results show that the procedure can realize real-time imaging under unknown wall characteristics,and also a relatively satisfactory image focusing is obtained.

through-the-wall imaging;parameter estimation;real time;support vector machine

2014-12-30;

2015-06-17；责任编辑：覃怀银

国家自然科学基金(No.61071022,No.61372045);江苏省自然科学基金项目(No.BK20140891);南京邮电大学大学生创新计划(No.XYB2015083);南京邮电大学科研基金(No.NY215165)

TN957

A

0372-2112 (2016)07-1613-06

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.07.014