基于迭代变步长LMS的数字域自干扰对消

刘建成，全厚德，赵宏志，唐友喜

(1.军械工程学院信息工程系，河北石家庄 050003； 2.电子科技大学通信抗干扰技术国家级重点实验室,四川成都 611731)

基于迭代变步长LMS的数字域自干扰对消

刘建成1，全厚德1，赵宏志2，唐友喜2

(1.军械工程学院信息工程系，河北石家庄 050003； 2.电子科技大学通信抗干扰技术国家级重点实验室,四川成都 611731)

针对同时同频全双工(Co-frequency and Co-time Full Duplex,CCFD)系统已有的数字域干扰对消方法收敛速度慢和对消比低的问题，本文提出了迭代变步长最小均方(Least Mean Square,LMS)算法，利用该算法实现了快速收敛的高对消比数字域干扰对消.首先，改进Logistic函数，缩短其函数值由大至小的变化区间，再利用该非线性函数计算随迭代次数变化的步长因子值，从而加快干扰对消的收敛速度，高精度递推估计自干扰信道参数，即获得高的对消比.最后，理论分析了该对消方法收敛性和计算复杂度，得到了稳态条件下对消比的闭合表达式.仿真表明，该方法与已有变步长LMS对消方法相比，对消比可增加6dB以上，收敛速度可提高1倍，与最小二乘信道估计干扰对消方法相比，对消比提高了至少10dB.

同时同频全双工；自干扰对消；变步长LMS

1　引言

目前无线频谱资源日益紧张，传统的频分双工(Frequency Division Duplexing,FDD)和时分双工(Time Division Duplexing,TDD)由于频谱和时间利用率低，传输速率受限[1]，已不能满足人们的需求.同时同频全双工(Co-frequency and Co-time Full Duplex,CCFD)技术在同等带宽下，理论上具有两倍于传统双工的传输速率[1,2]，克服了传统双工频谱资源浪费和传输速率低的不足，已受到广泛关注.CCFD技术实现必须建立在自干扰有效消除基础上，需具有110dB以上的自干扰抑制能力[2]，目前主要通过天线隔离抑制，模拟和数字域自干扰对消三种途径解决.

天线隔离抑制主要是通过对收发天线位置和方向性的设计，增加收发通道间的隔离度，降低自干扰信号与期望信号功率比值，可实现25～40dB的抑制比[3～5].模拟域自干扰对消是在接收天线至低噪放之间进行干扰消除，能够保证接收通道不被阻塞，同时降低对ADC(Analog Digital Convert)器件量化位数和动态范围的要求[6]，减小ADC器件对期望信号的影响[7].但是由于模拟器件可控性受限，目前只能实现40～50dB的对消[8,9]，并不能够有效抑制，所以在数字域进一步消除自干扰，提高最终的干扰对消比(Interference Cancellation Ratio,ICR)，是实现CCFD技术必不可少的关键环节[10,11].

数字域自干扰对消主要有信道估计和自适应滤波两类方法.文献[1,2]均是基于信道估计进行数字域干扰消除，文献[1]采用常规时域等间隔导引序列估计信道响应，文献[2]利用WiFi中OFDM信号每帧的导引序列估计出自干扰信号参数，不过该方法受限于帧结构中导引序列设置.文献[11]给出了基于最小均方误差的直通和共轭两路信道参数估计方法，进而实现宽带自干扰信号的数字对消，不过该方法同样需要导引信号，且不能实时跟踪信道的变化.文献[12]针对中继通信的CCFD，提出了基于谱成型LMS反馈干扰对消方法，但该方法计算复杂，收敛速度与对消比相互制约.

综上所述，现有CCFD数字域自干扰对消方法多采用常规信道估计，需进行矩阵的求逆和分解运算，计算复杂，且在一定持续时间内不能实时跟踪自干扰信道参数的变化.针对数字域自干扰对消存在的以上问题，本文提出了基于迭代变步长LMS(Iterative Variable Step-size LMS,IVSSLMS)算法的对消方法.该方法利用改进Logistic非线性函数，建立LMS步长因子与时间(等价为算法的递推次数)的内在关系，在保证稳态失调误差较小情况下(即高的ICR)有效提高算法收敛速度，实现数字域的自干扰对消.仿真结果显示，在天线隔离和模拟域干扰对消基础上，该方法可有效估计自干扰信道等效参数，当干噪比为50dB、35dB时ICR分别能够达到45dB、34dB以上.

2　CCFD数字域自干扰对消原理

CCFD技术基本结构如图1所示[2]，图中模拟和数字域干扰对消是实现CCFD必不可少的环节，其关键在于如何利用发送通道的射频信号sRF(t)和数字基带信号s(n)最大限度地消除接收端r(t)中的自干扰信号sI(t).

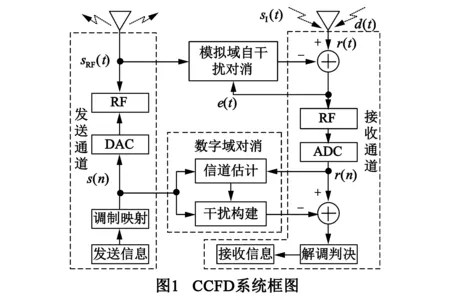
图1所示的数字域自干扰对消是采用信道估计的方法.接收通道的数字基带信号向量可表示为[1,2]：

r(n)=sI(n)+d(n)+ε(n)=s(n)hM+d(n)+ε(n)

(1)

其中，r(n)为模拟域干扰对消后的L×1维接收信号向量，sI(n)为模拟域干扰对消后残余的L×1维自干扰信号向量，d(n)为期望信号，ε(n)为加性噪声，二者均为L×1维.hM表示M阶自干扰信道响应，为M×1维.s(n)为发送通道数字基带信号构成的L×M维Toeplitz矩阵[2].

(2)

(3)

其中，上标H表示矩阵(向量)共轭转置.

式(3)需矩阵相乘和求逆运算，计算较复杂，通常需在时域或频域插入导引序列，占用额外带宽，且应对信道突变的能力有限.所以，可采用计算简单的LMS算法递推求解自干扰信道向量hM，进而实现数字域自干扰消除.

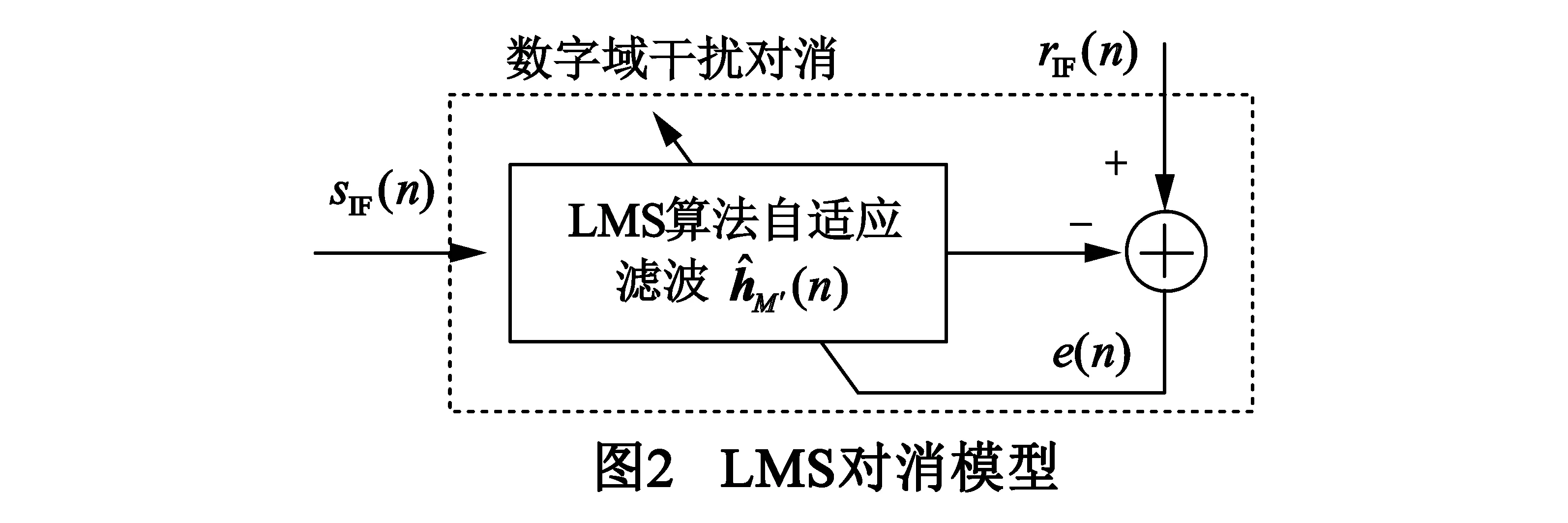
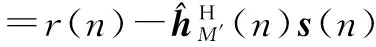
(4)

(5)

其中，e(n)为对消后信号，即LMS算法的反馈误差，d(n)和ε(n)同式(1)，分别为期望信号和加性噪声，(-)表示取共轭，sI(n)表示接收的数字基带干扰信号，可等价于发送信号s(n)通过M阶离散线性信道h(n)，即：

(6)

3　基于IVSSLMS的数字域自干扰对消

由文献[18,19]知，采用自适应滤波方法估计自干扰信道响应必须解决收敛速度和稳态失调误差相互制约的问题.因此，本节提出迭代变步长LMS算法，在保证获得高ICR下，有效提高对消方法的收敛速度.

LMS算法收敛时间τ随步长因子μ的增大(满足收敛条件)而减少，但稳态失调误差ξ会随μ的增大而增大.因此，文献[16,20～22]提出了变步长方法，使得步长因子μ在算法初始阶段具有较大值以提高收敛速度，在接近收敛时变小以降低稳态失调误差.不过，已有的变步长方法容易受相关噪声等因素影响.为弥补该不足，提出迭代变步长方法，步长因子μ随递推次数的增加逐渐迭代减小，不受控于反馈误差信号，从而有效提高ICR.

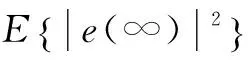
(7)

(8)

其中，Jmin为不可消除的外界干扰，比如系统噪声等.

迭代变步长LMS算法为使步长因子μ满足式(7)所示的收敛条件，且在收敛时具有小的稳态失调误差，对步长因子取值加以限定.再依据改进Logistic函数建立与递推次数n间的非线性关系，如下所示：

(9)

其中，μmin是设定的最小值，μmax是由式(7)设定的最大值，κ为调整参数，控制了μ(n)随n变换的快慢，m是步长因子改变的起始时刻，初始值为0.由表达式可知μ(n)随n单调递减，变换趋势如图3所示.

(10)

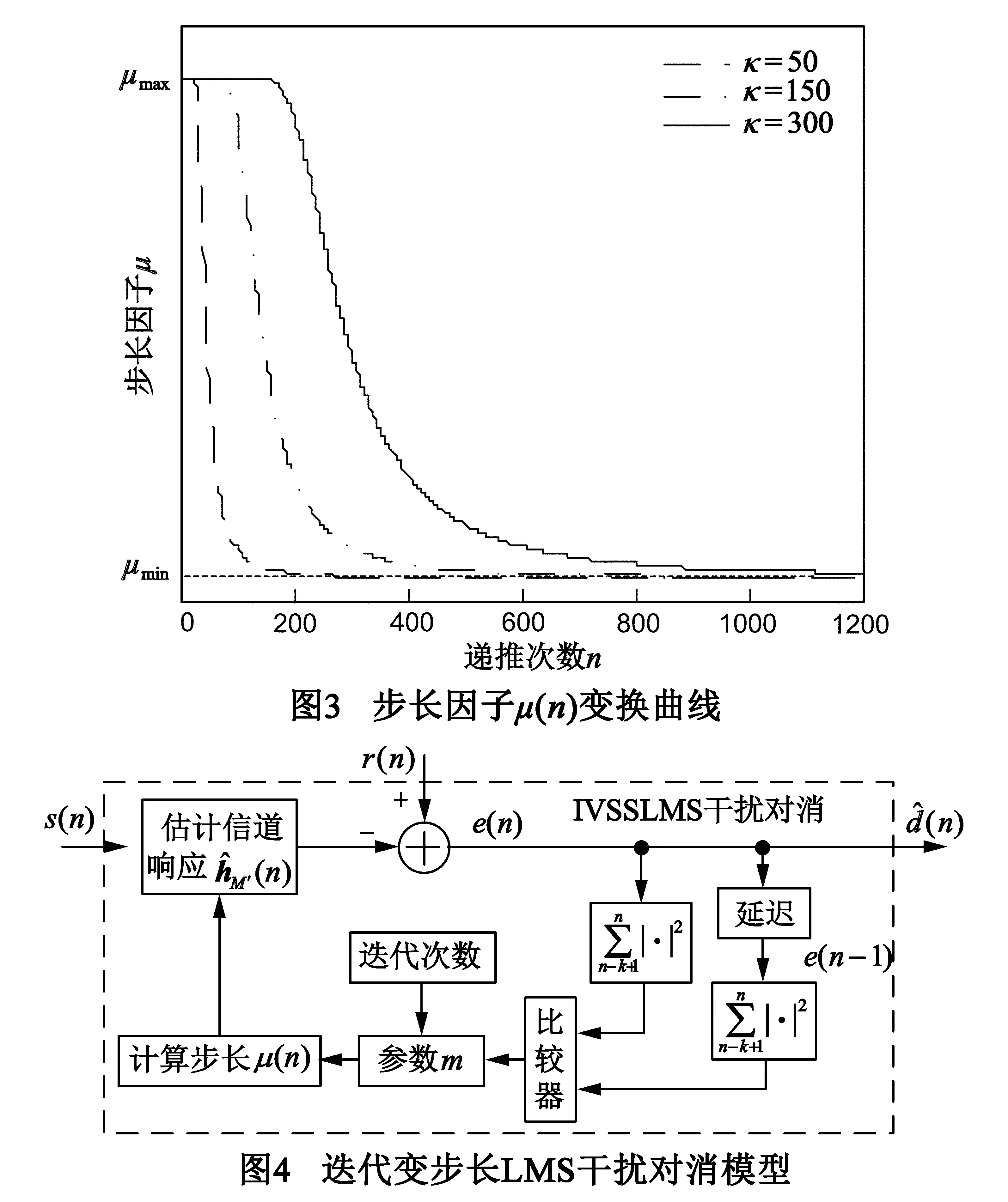
为IVSSLMS算法具有应对自干扰信道hM突变的能力，步长因子随递推次数迭代改变的同时，通过检测前后时刻对消后信号功率，判断hM是否发生突变.在此基础上，本文对消方法模型如图4所示，基本流程如下：

(1)算法初始，根据已知发送信号s(n)及相应先验知识，设阶数M′，保证M′不小于自干扰信道等效阶数M，设步长因子的最大值μmax、最小值μmin和κ，起始时刻m=0，即递推次数n由0起始；

(2)将(1)中参数代入式(9)，计算步长因子μ(n)，之后执行式(4)和(10)；

(3)估计当前时刻误差e(n)的功率大小，与前一时刻e(n-1)比较，若大于设定的门限值χ，则执行步骤(4)，小于则直接返回执行步骤(2)；

(4)将当前的递推次数n赋值给m，返回执行步骤(2).其中，χ设为噪声和期望信号功率之和的两倍.误差信号功率估计可等价求k个值的平均，计算如下：

(11)

4　算法性能分析

本节将从理论上分析基于IVSSLMS数字域自干扰对消方法的收敛性和稳态下对消比，推导步长因子与收敛速度关系式，稳态ICR的最终表达式.另外，对比了本文算法与已有VSSLMS及LS信道估计干扰对消法的复杂度.

4.1算法收敛性和对消比分析

(12)

(13)

e(n)=cH(n)s(n)+d(n)+ε(n)

(14)

将式(14)代入式(13)得：

+2cH(n)s(n)[d(n)+ε(n)]

(15)

由于ε(n)和d(n)统计独立，且与信号向量s(n)不相关，利用直接平均法[19]可得：

(16)

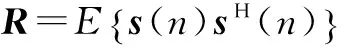
(17)

再令C(n)=UHc(n)，根据式(10)和(14)可得：

C(n)=UHc(n-1)-μ(n-1)UHs(n-1)

·[sH(n-1)c(n-1)+d(n-1)+ε(n-1)]

=[I-μ(n-1)Λ]C(n-1)-μ(n-1)

·UHs(n-1)[d(n-1)+ε(n-1)]

(18)

由式(17)可得R=UΛUH，又因c(n)=UC(n)，将二者代入式(16)，可得：

(19)

因输入信号向量s(n)与期望信号d(n)、白噪声ε(n)不相关，可化简得：E{|e(n)|2}=E{CH(n-1)Λ[I-μ(n-1)Λ]2C(n-1)}

(20)

其中tr(·)表示求矩阵的迹.以此类推，有：

E{|e(n)|2}=E{CH(0)ψ(n)C(0)}

(21)

其中，

(22)

(23)

由于酉矩阵不改变矩阵的迹，整理得：

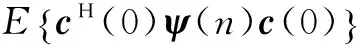
(24)

可等价于：

(25)

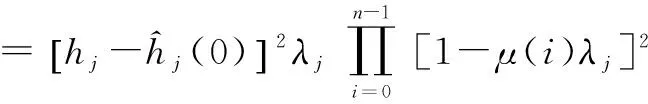
0≤j≤M-1(26)

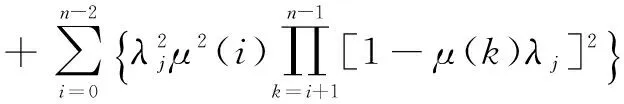
0≤j≤M-1(27)

可见式(25)收敛条件为，对于任意i和j均有|1-μ(i)λj|<1，与式(7)所示的LMS收敛条件相符.下面根据式(25)～(27)，与定步长LMS(Fixed Step-size LMS,FXSSLMS)算法对比收敛性能.

由上述分析知，算法收敛性取决于式(26)中累积乘积取值的变化趋势，对于FXSSLMS算法μ(i)为定值，故本文算法和FXSSLMS的收敛因子分别为ρIVSS(n)和ρFXSS(n)：

(28)

ρFXSS(n)=(1-μλ)2n

(29)

设最大特征λmax=1，FXSSLMS算法的步长因子为μ=0.1/λmax，本文算法中μmax=8μ、μmin=0.5μ，则两种算法的理论收敛曲线如图5所示.对于一般情况，当ρ(n)<10-30时均可近似为0，由图可见本文算法的收敛速度明显快于FXSSLMS算法.

(30)

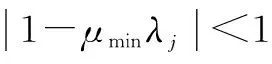
(31)

又因n→∞时步长因子μmin满足：μminλmax<<1，即2-μminλmax≈2，故式(31)可进一步近似为：

(32)

(33)

在上述分析基础上，可由发送信号s(n)功率和信道响应向量维数M估计出s(n)自相关矩阵的最大特征值，设定步长因子最大值μmax=0.8/λmax，同时参考式(33)设定步长因子最小值.另外，式(9)中参数κ值依据实际情况而定，过大和过小均易导致不能在最短时间内收敛到最高ICR，降低算法的性能.当ρIVSS(n)小于10-30可认为算法处于收敛状态，结合图5所示的其变化趋势可知，若兼顾收敛速度和ICR，则算法收敛时刻，即ρIVSS(n)≤10-30时步长因子应处在变化最快的区域，即图3中曲线斜率最大处.所以，迭代变步长式(9)中的参数κ需满足以下两个关系式：

(34)

4.2复杂度分析

除算法收敛速度和稳态ICR外，计算复杂度也是影响其应用的重要因素.现分析IVSSLMS算法计算复杂度，并与文献[21,22]中VSSLMS算法和基于LS信道估计对消方法进行对比.假设算法中递推估计变量的维数为M，式(9)的指数运算一般采用查表法，可以暂不考虑其运算量.对于LS信道估计对消方法，若式(2)中已知干扰信号矩阵为L×M维，且设每间隔NL个信号数据进行一次估计，M×M维矩阵求逆需2(M3-M)/3次加法和2(M3-M)/3次乘法，则本文方法、文献[21,22]方法和LS估计法输出NL个期望信号数据所需的加、乘和除法次数如表1所示.

表1　不同方法所需的计算次数

5　仿真验证

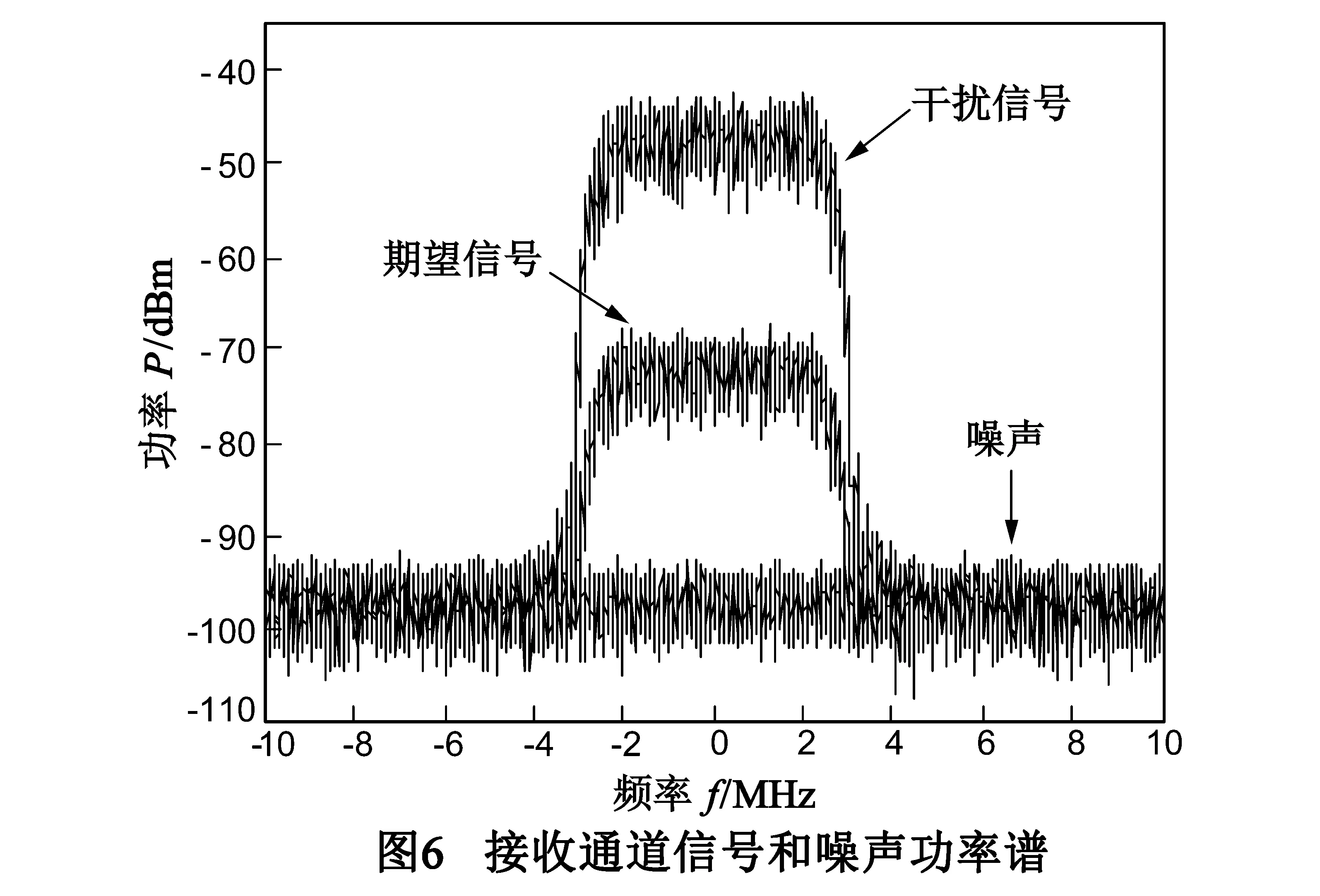
本节将仿真所提出的数字域干扰对消方法，并与已有VSSLMS算法和基于常规信道估计对消方法进行对比.仿真以速率为10Mbps的QPSK调制为例，暂不考虑非线性和ADC量化噪声影响.参考文献[2,17]，假设接收通道噪声限为-95dBm，自干扰信号经天线隔离和模拟域对消后为-45dBm，期望信号为-70dBm，即INR(Interference-to-Noise Ratio)和SIR(Signal-to-Interference Ratio)分别为50dB和-25dB，接收通道各信号频谱如图6所示.参考文献[23,24]，设仿真自干扰信道为莱斯信道，总传播路径个数为4，包括3条多径，对应K因子、路径时间和损耗(dB)分别为：[1 2 0.5 0.02],[2.5 4 7 10]/fs,[-15 -29 -46 -53]，其中fs为调制后的符号速率.为进一步表示算法的收敛速度，将对消比ICR达到一定值所需的迭代次数n等价转换为时间τ，根据设置的仿真条件计算一个基带符号持续时间TΔ=1/fs，若忽略算法中向量相乘等运算所需时间，则τ=nTΔ.另外，本节所有结果均是由200次蒙特卡罗仿真实验所得.

5.1与VSSLMS方法对比分析

在上述仿真条件下，对比本文IVSSLMS算法与文献[21,22]的VSSLMS算法，分析其收敛性与稳态的ICR.因干扰信道响应hM等效阶数未知，由先验条件设定算法的阶数M′，保证M′≥M，取M′=26.设信号s(n)和r(n)功率已归一化，同时为避免步长因子过大和信号自相关矩阵特征值扩散导致的算法发散[18]，令本文算法和文献[21]的μmax=0.02，文献[22]VSSNLMS算法步长因子最大值为1，其步长因子最小值分别取0.005和0.05两种情况.参考文献[21,22]参数设置原则，三种算法具体参数如表2所示.

表2　不同方法对应参数

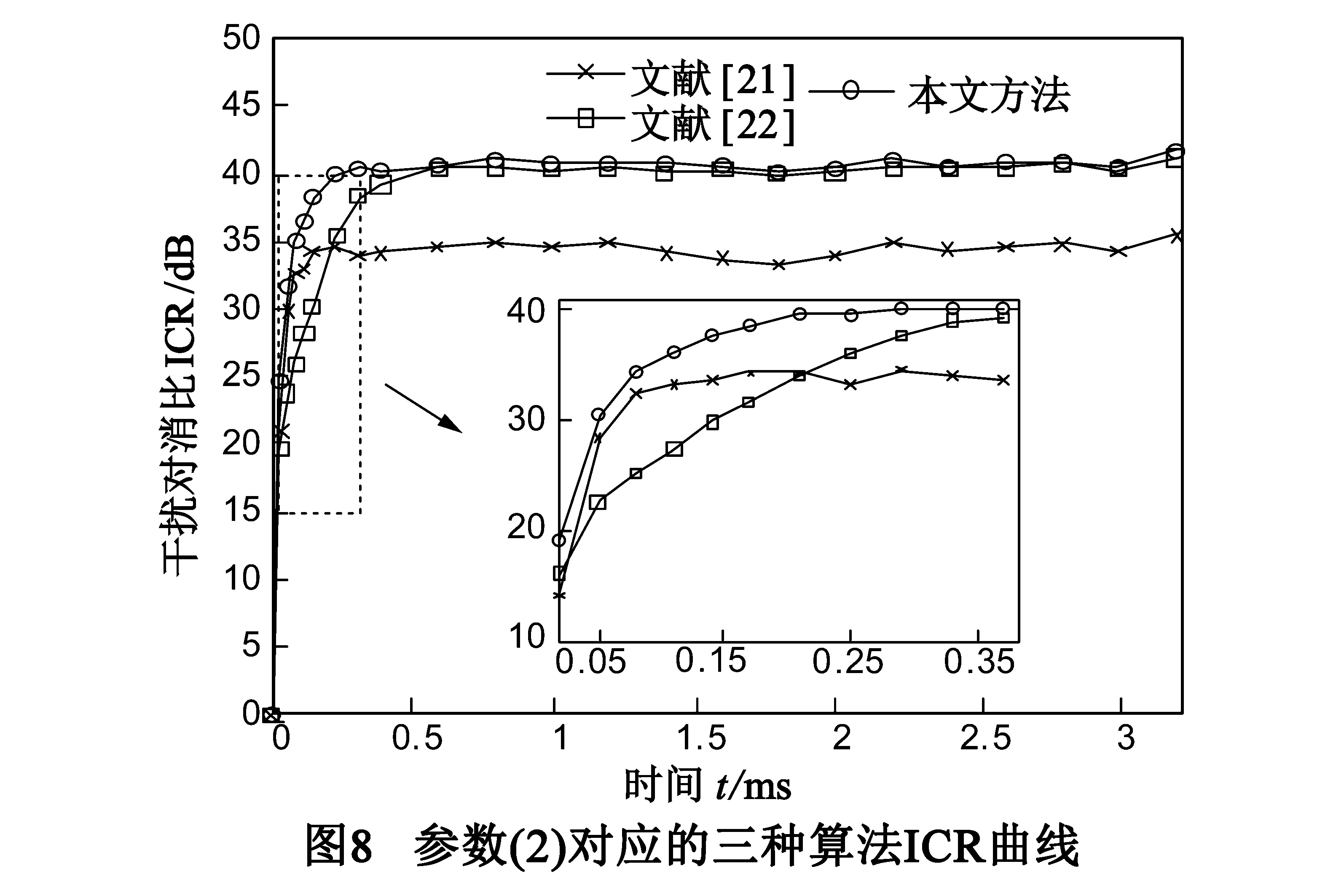
统计平均200次独立仿真结果，得三种算法ICR收敛曲线，参数(1)、(2)对应结果分别如图7、8和表3所示.由图7和表3可见，参数(1)下本文IVSSLMS算法与文献[22]相比，稳态的ICR有略微提高，但ICR达到38dB所需收敛时间缩短了近一倍；与文献[21]相比，38dB对消比所需收敛时间缩短了约十分之一，但稳态的ICR提高了8dB以上.由图8和表3可见，参数(2)对应的本文算法与文献[22]相比，稳态ICR相近，但ICR达到32dB所需收敛时间缩短了两倍以上；与文献[21]相比，在保证未降低收敛速度情况下，稳态ICR提高了6dB以上.可见，本文算法即具有快的收敛速度，又具有高的ICR，且与已有VSSLMS算法相比得到了明显提升.另外，根据本文算法步长因子最小值，图7、图8中收敛曲线变化趋势，和表3的稳态ICR，可发现最终ICR将相差10dB(由于仿真时间较短，图7并未达到完全收敛状态)，从而验证式(33)的正确性，步长因子最小值也影响了收敛速度，与式(28)和(30)相对应.

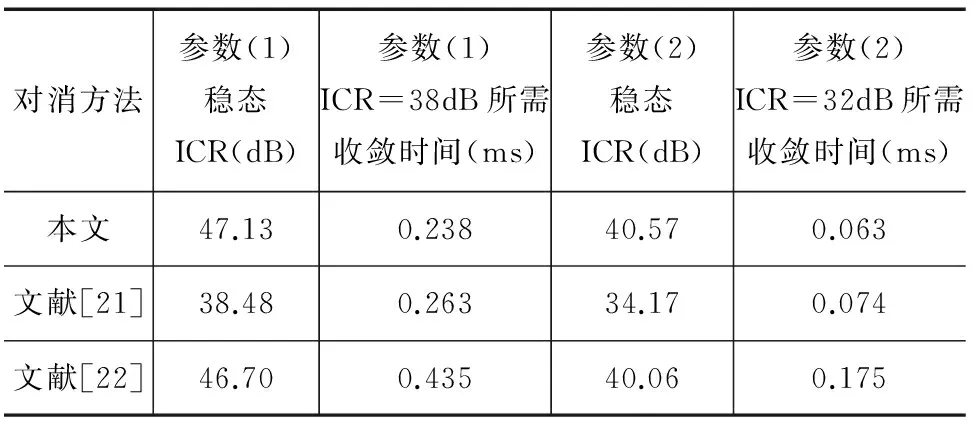
表3　两种参数仿真结果对比

另一方面，为分析参数κ对算法性能的影响，再分别以150，300，500和800进行仿真对比，结果如图9所示.结合图5可知，当κ较小时步长因子较早变为μmin，致使收敛速度降低，而当κ过大时步长因子较长时间保持μmax，致使出现阶段性收敛，影响了整体性能的提升.可见κ取值应根据式(34)采取折中的原则，即能保证快速达到稳态，又可避免阶段性收敛，在本文仿真条件下κ=200较为适宜.

5.2与基于LS信道估计对消方法的对比

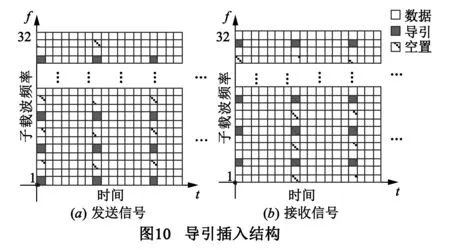
在5.1节仿真条件基础上，假定t1=1.195ms和t2=3.195ms时刻自干扰信道分别变为：K因子[0.5 0.05 1.5 0.2]，时延[2 6 8 12]/fs,衰减[0 -20 -34 -40]；K因子[0.01 3 0.8 0.01]，时延[3 5 9 11]/fs，衰减[-3 -13 -30 -45].为与基于LS信道估计对消方法(简称LS估计法)对比，参考文献[25,26]以疏状形式插入导引序列，以子载波个数为32的OFDM为例，为避免期望信号影响自干扰信号的信道估计，二者导频插入不同子载波处，分别如图10(a)和(b)所示.

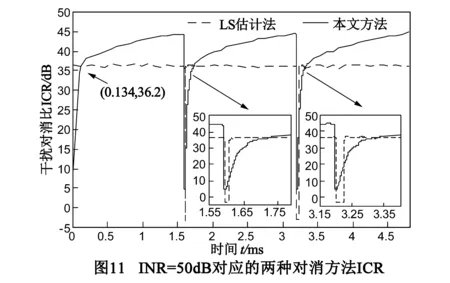
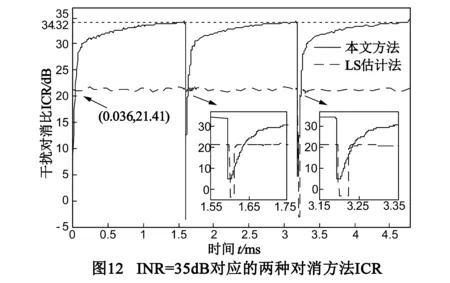
本文方法设置与5.1节参数(1)相同，为对比不同情况下两种对消方法性能，另增设仿真条件：接收通道噪声限为-95dBm，自干扰信号为-60dBm，期望信号为-80dBm，即INR、SIR分别为35dB和-20dB.INR为50dB、35dB的仿真结果分别如图11和12所示.由图11和12可见，LS估计法因信道突变引起的对消比恶化较本文方法推迟了一段时间，这是因为LS估计法导引序列占用了相应的时隙.对比t1和t2时刻对消比恶化持续时间，可以发现信道突变发生在不同时刻将导致LS估计法ICR恶化的持续时间不同，这是因为信道突变影响的是该时刻至下一个导引序列估计的这段时间，而本文方法的重新收敛并不受信道突变时间的影响.分析图11，在高干噪比INR=50dB时，本文方法在0.134ms后ICR高于LS估计法，稳态ICR比LS估计法提高了约10dB.由图12可知，干噪比INR=35dB时，本文方法在0.036ms后ICR即高于LS估计法，LS估计法在该干噪比下性能下降明显，达到的ICR只有约21.5dB，而本文方法的稳态ICR仍达到34.42dB，提高了约13dB.由以上分析可见，本文方法与LS估计法相比，能够有效提高稳态ICR，尤其是能够克服低干噪比下ICR恶化的问题.

由本节的仿真及分析可知，本文基于IVSSLMS的数字域自干扰对消方法即具有快的收敛速度，又能够获得高的稳态ICR，且具有较好的跟踪能力，优于已有VSSLMS算法.与基于LS信道估计的对消方法相比，既降低了计算复杂度，又提高了ICR.

6　总结

本文针对CCFD数字域自干扰消除问题，给出了基于迭代变步长LMS算法的对消方法，通过递推次数迭代控制LMS算法步长因子大小，既有效提高了对消方法的收敛速度，又获得高的干扰对消比，同时计算复杂度也低于已有变步长LMS算法.另外，与常规信道估计的对消方法相比，克服了低干噪比下对消比严重恶化的不足，能够改善10dB以上.所以，本文提出的数字域干扰对消方法既具有快的收敛速度，又能够获得高的对消比，且有利于数字硬件实现，具有较高的实际应用价值.不过，本文暂时未考虑ADC器件引起的非线性问题，仍需进行更为深入的研究.

[1]Melissa D,Chris D,Ashutosh S.Experiment-driven characterization of full-duplex wireless systems[J].IEEE Transactions on Wireless Communications,2012,11(12):4296-4307.

[2]Dinesh B,Emily M,Sachin K.Full duplex radios[J].ACM SIGCOMM Computer Communication Review,2013,43(4):375-386.

[3]Knox M E.Single antenna full duplex communications using a common carrier[A].Wireless and Microwave Technology Conference[C].Cocoa Beach:IEEE,2012.1-6.

[4]Radunovic B,Gunawardena D,Key P,et al.Rethinking indoor wireless mesh design:Low power,low frequency,full-duplex[A].IEEE Workshop on Wireless Mesh Networks[C].Boston:IEEE,2010.1-6.

[5]Choi J I,Jain M,Srinivasan K,et al.Achieving single channel,full duplex wireless communication[A].Proceedings of the Sixteenth Annual International Conference on Mobile Computing and Networking[C].Chicago:ACM,2010.1-12.

[6]Riihonen T,Wichman R.Analog and digital self-interference cancellation in full-duplex MIMO-OFDM transceivers with limited resolution in A/D conversion[A].2012 Conference Record of the Forty-Sixth Asilomar Conference on Signals,Systems and Computers[C].Pacific Grove:IEEE,2012.45-49.

[7]张志亮,罗龙,邵世海,等.ADC量化对同频全双工数字自干扰消除的误码率性能分析[J].电子与信息学报,2013,36(6):1331-1337.

Zhang Zhiliang,Luo Long,Shao Shihai,et al.Analysis of ADC quantizing affection on SER performance of self-interference canceling common-frequency full-duplex system[J].Journal of Electronics & Information Technology,2013,36(6):1331-1337.(in Chinese)

[8]Jain M,Choi J I,Kim T,et al.Practical,real-time,full duplex wireless[A].Proceedings of the 17th Annual International Conference on Mobile Computing and Networking[C].Las Vegas:ACM,2011.301-312.

[9]Zhaojun H,Shihai S,Ying S,et al.Performance analysis of RF self-interference cancellation in full-duplex wireless communications[J].IEEE Wireless Communications Letters,2014,3(4):405-408.

[10]Debaillie B,van den Broek D J,Lavin C,et al.Analog/RF solutions enabling compact full-duplex radios[J].IEEE Journal on Selected Areas in Communications,2014,32(9):1662-1673.

[11]Korpi D,Anttila L,Syrjala V,et al.Widely-linear digital self-interference cancellation in direct-conversion full-duplex transceiver[J].IEEE Journal on Selected Areas in Communications,2014,32(9):1674-1687.

[12]Lopez-Valcarce R,Antonio-Rodriguez E,Mosquera C,et al.An adaptive feedback canceller for full-duplex relays based on spectrum shaping[J].IEEE Journal on Selected Areas in Communications,2012,30(8):1566-1577.

[13]Schüldt C,Lindstrom F,Li H,et al.Adaptive filter length selection for acoustic echo cancellation[J].Signal Processing,2009,89(6):1185-1194.

[14]Wada T S,Juang B H.Enhancement of residual echo for robust acoustic echo cancellation[J].IEEE Transactions on Audio,Speech,and Language Processing,2012,20(1):175-189.

[15]Contan C,Kirei B S.Modified NLMF adaptation of Volterra filters used for nonlinear acoustic echo cancellation[J].Signal Processing,2013,93(5):1152-1161.

[16]Mader A,Puder H,Schmidt G U.Step-size control for acoustic echo cancellation filters-an overview[J].Signal Processing,2000,80(9):1697-1719.

[17]Melissa D.Full-duplex wireless:design,implementation and characterization[D].Houstin:Rice University,2012.

[18]Simon H.自适应滤波器原理(第四版,郑宝玉译)[M].北京：电子工业出版社，2010.206-212.

[19]Zhang S,Zhang J.New steady-state analysis results of variable step-size LMS algorithm with different noise distributions[J].IEEE Signal Processing Letters,2014,21(6):653-657.

[20]Mayyas K.Performance analysis of the deficient length LMS adaptive algorithm[J].IEEE Transactions on Signal Processing,2005,53(8):2727-2734.

[21]Huang B,Xiao Y,Sun J,et al.A variable step-size FXLMS algorithm for narrowband active noise control[J].IEEE Transactions on Audio,Speech,and Language Processing,2013,21(2):301-312.

[22]Huang H C,Lee J.A new variable step-size NLMS algorithm and its performance analysis[J].IEEE Transactions on Signal Processing,2012,60(4):2055-2060.

[23]吴翔宇,沈莹,唐友喜.室内环境下2.6GHz同时同频全双工自干扰信道测量与建模[J].电子学报,2015,43(1):1-6.Wu Xiangyu,Shen Ying,Tang Youxi.Measurement and modeling of co-time co-frequency full-duplex self-interference channel of the indoor environment at 2.6GHz[J].Acta Electronica Sinica,2015,43(1):1-6.(in Chinese)

[24]Hashemi H.The indoor radio propagation channel[J].Proceedings of the IEEE,1993,81(7):943-968.

[25]Arslan H.Channel estimation for wireless OFDM systems[J].IEEE Surveys and Tutorials,2007,9(2):18-48.

[26]Shen Y,Martinez E.Channel estimation in OFDM systems[J].Application Note,Freescale Semiconductor,2006.

刘建成男,1987年7月出生,河北邱县人.2010年毕业于解放军电子工程学院通信对抗工程专业，并于本校攻读硕士研究生，2013年考入解放军军械工程学院，攻读导航制导与控制工程专业博士研究生，主要进行超短波无线通信抗干扰的有关研究.

E-mail:liujiancheng1987@126.com

全厚德男,1963年生,辽宁人.现为解放军军械工程学院信息工程系教授，博士生导师.研究方向主要包括：无线通信技术、指挥控制系统、通信设备性能测试等.

Digital Self-Interference Cancellation Based on Iterative Variable Step-Size LMS

LIU Jian-cheng1,QUAN Hou-de1,ZHAO Hong-zhi2,TANG You-xi2

(1.Department of Information Engineering,Ordnance Engineering College of PLA,Shijiazhuang,Hebei 050003,China; 2.National Key Laboratory of Science and Technology on Communications,University of Electronic Science andTechnology of China,Chengdu,Sichuan 611731,China)

Recently,the co-frequency co-time full duplex (CCFD) has been widely studied for its higher spectral efficiency.However,it must avoid the strong co-channel self-interference to put this technology into practice,and the existing digital interference cancellation methods usually have slow convergence and small cancellation-ratio.Considering this obstacle,the digital cancellation method based on iterative variable step-size least mean square algorithm (IVSSLMS) is proposed in this paper.Firstly,the function of Logistic is modified to accelerate its tendency for value changing lower.Then,the iterative variable step-size is obtained through the modified nonlinear function.Consequently,convergence of interference cancellation is speeded up,and accurate parameters of self-interference channel are estimated to achieve high cancellation-ratio is derited.Finally,the convergence and complexity of this digital interference cancellation method are analyzed and the closed expression of steady-state cancellation-ratio is derived.Simulations verify that the cancellation-ratio of this method could achieve more than 6dB and 10dB in comparison with the existing variable step-size LMS methods and cancellation method based on least square channel estimation respectively,and the convergence speed could be enhanced doubled.

co-frequency and co-time full duplex;self-interference cancellation;variable step-size LMS

2015-02-25;

2015-09-23;责任编辑：李勇锋

国家自然科学基金(No.61531009,No.61271164,No.61471108,No.61201266,No.61501093);重大专项(No.2014ZX03003001-002);国家863高技术研究发展计划(No.2014AA01A704,No.2014AA01A706,No.2015AA01A701);国家电网公司科技项目(No.SGSCDKJLZJKJ1400099)

TN911.72

A

0372-2112 (2016)07-1530-09

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.07.002