DNA纳米颗粒共聚体在图的连通度问题中的应用

王艳钗，张　会，董亚非,

(1.陕西师范大学计算机科学学院，陕西西安 710119； 2.陕西师范大学生命科学学院，陕西西安 710119)

DNA纳米颗粒共聚体在图的连通度问题中的应用

王艳钗1，张会2，董亚非1,2

(1.陕西师范大学计算机科学学院，陕西西安 710119； 2.陕西师范大学生命科学学院，陕西西安 710119)

本文提出了一种利用DNA纳米金颗粒共聚体的自组装过程解决图论中一个NP完全问题—连通度问题的DNA计算方法，构建了解决图的连通度问题的三维DNA自组装计算模型.根据设计的算法，首先需要根据具体的图的连通度问题设计用于自组装的DNA纳米金颗粒共聚体，然后根据算法经过一系列实验设计来求解连通度问题.本文利用Visual DSD仿真该实验的可行性，为下一步DNA自组装计算模型的应用提供了可行的方案.

DNA计算；DNA纳米金颗粒；图的连通度；三维模型

1　引言

1994年，Adleman[1]首次利用线性DNA 分子解决了一个7个顶点的Hamilton路问题.随后，许多科学家的目光被吸引到分子计算领域.1995年，Lipton[2]建立了解决可满足问题的DNA计算机.两年后，Ouyang等[3]提出了解决最大团问题的DNA计算模型.最近，张成[4,5]利用环形DNA分子求解了最大团问题同时利用自组装DNA链置换设计分子逻辑计算模型.以上方法都是利用DNA分子计算NP完全问题.近年来，很多研究学者提出了利用如RNA[6]、质粒[7]和瓦片[8,9]等多种不同的分子作为工具进行计算.2007年，Brun[10]利用瓦片进行了加法和乘法运算.目前利用DNA自组装引导纳米粒子形成三维纳米结构的技术极大地推进了许多基础科学问题的研究.Yan[11]设计出了用DNA纳米金颗粒共聚体的自组装过程构建纳米金颗粒三维管状结构的方法，通过控制纳米金颗粒的大小，可以分别形成叠环、单螺旋、双螺旋和嵌套螺旋等不同的结构.Alivisatos[12]报道了构建纳米金颗粒三维结构的方法，他们利用DNA链修饰的纳米金颗粒自组装形成金字塔结构，通过调节金字塔四个顶点的纳米金颗粒的大小，构建了纳米金颗粒的三维手性结构.2012年，杨玉星等[13]提出一种解决Ménage问题的粘贴DNA算法并简要分析了该算法的复杂度.2013年，李肯立[14]DNA自组装模型来求解N皇后问题的DNA计算方法.算法通过减少实验操作步骤数，降低了生化解的错误率.

最近，DNA自组装和DNA/AuNP被广泛应用在逻辑门和数字环路的设计，2010年，张成等[15]建立了一个基于环状DNA的逻辑门系统.证明了逻辑结果容易通过荧光信号和纳米金组装进行检测.2011年，张成等[16]构建了一个逻辑模型，该模型能够用于H1N1病毒基因的检测.2011年，Qian和 Winfree等[17]实验性的论证了数个数字逻辑环路.解决了一个由130条DNA链组成的在4-位(bit)平方根环路的问题.2013年，杨静等[18]利用纳米金颗粒构建了一个“YES”和“AND”的逻辑门.2014年，张成等[19]建立了一个基于环状DNA用纳米金颗粒来控制链置换过程.

本文提出了一种利用DNA纳米金颗粒共聚体的自组装过程解决图论中一个NP完全问题—连通度问题的DNA计算方法，构建了解决图的连通度问题的三维DNA自组装计算模型.根据设计的算法，首先需要根据具体的图的连通度问题设计用于自组装的DNA纳米金颗粒共聚体，然后根据算法经过一系列实验过程来求解连通度问题.另外还通过了Visual DSD和NUPACK对该生物实验进行了仿真，来说明该实验的可行性.与传统的电子计算机相比，降低了计算的复杂度，所使用的生物化学实验技术也很成熟且便于操作，为下一步DNA自组装计算模型的应用提供了可行的方案.

2　基于DNA纳米颗粒共聚体分子算法

2.1连通度问题

连通度问题是图论中的一个NP完全问题,它对于构造可靠通讯网络有很重要的意义，由于它与网络模型和组合优化有密切关系,因此具有很重要的理论和应用价值.

定义1若G≠Kp是一个连通图，φ≠V1⊂V(G)，若G-V1非连通，则称V1是图G的顶点割.若顶点割V1含k个顶点，也称V1是k顶点割.

设G是p阶连通图，令

(1)

称κ(G)为G的连通度.

定义2若G≠Kp是一个连通图，φ≠E1⊆E(G)，若G-E1非连通，则称E1是图G的边割.若边割E1含k条边，也称E1是k边割.

设G是p阶连通图，令

(2)

称λ(G)为G的边连通度.从而一个非平凡连通图的边连通度就是使这个图成为非连通图所需要去掉的最小边数.

定理1G是p阶简单图，则以下几条结论成立：

(1)κ(G)≤δ(G)，λ(G)≤δ(G)；

(2)κ(G)≤p-1，等号成立当且仅当G≅Kp；

(3)λ(G)≤p-1，等号成立当且仅当G≅Kp;

(4)对G的任意一个顶点u，κ(G)-1≤κ(G-u)；

(5)对G的任意一条边e，λ(G)-1≤λ(G-e)≤λ(G).

引证1若G是p阶简单图，由定理1知λ(G)≤δ(G)；

假设G是连通的非完全图.设λ(G)是一个最小边割，则恰好有两个连通分支，记为G1和G2，并且G1与G2分别存在一个顶点u∈V(G1)和v∈V(G2)，使uv∉E(G)，否则，p(G1)=p1，p(G2)=p2=p-p1，有

λ(G)=|E1|≥p1(p-p1)≥p-1

由定理1，知G≅Kp，与假设矛盾.

现取G的一个点子集：V1={ui/ui是不同与u和v且与ei关联的一个顶点，i=1,2,…,λ(G)}则|V1|≤|E1|=λ(G)，并且在G-V1中不存在(u-v)路，所以V1是G的一个顶点.故κ(G)≤|V1|≤λ(G)

∴

κ(G)≤λ(G)≤δ(G)

(3)

严格成立.其中δ(G)是G的顶点的最小度.求解图的连通度目前没有有效的算法,主要采用最大流算法求解图的边连通度,而对于点连通度目前没有很好的算法[20].但是，2004年，马润年等[21]基于质粒技术的无向图的最大权团问题的DNA算法,依据Head T等的实验手段，解决了最大团问题，方刚[22]用三维DNA图结构设计了一种生物算法求解图的连通度，张社民[23,24]用类似的结构设计了一种生物进化算法.这给我们求解连通度提供了一个种新的思路.本文利用DNA纳米金颗粒共聚体的自组装过程解决连通度问题，构建了解决图的连通度问题的三维DNA自组装计算模型.

2.2DNA纳米颗粒共聚体算法

用DNA纳米颗粒共聚体自组装计算模型解决图的连通度问题，根据具体的图的顶点和边设计所需的DNA纳米金颗粒共聚体上DNA链的具体数目和碱基序列，以完成自组装形成所需要的结构.

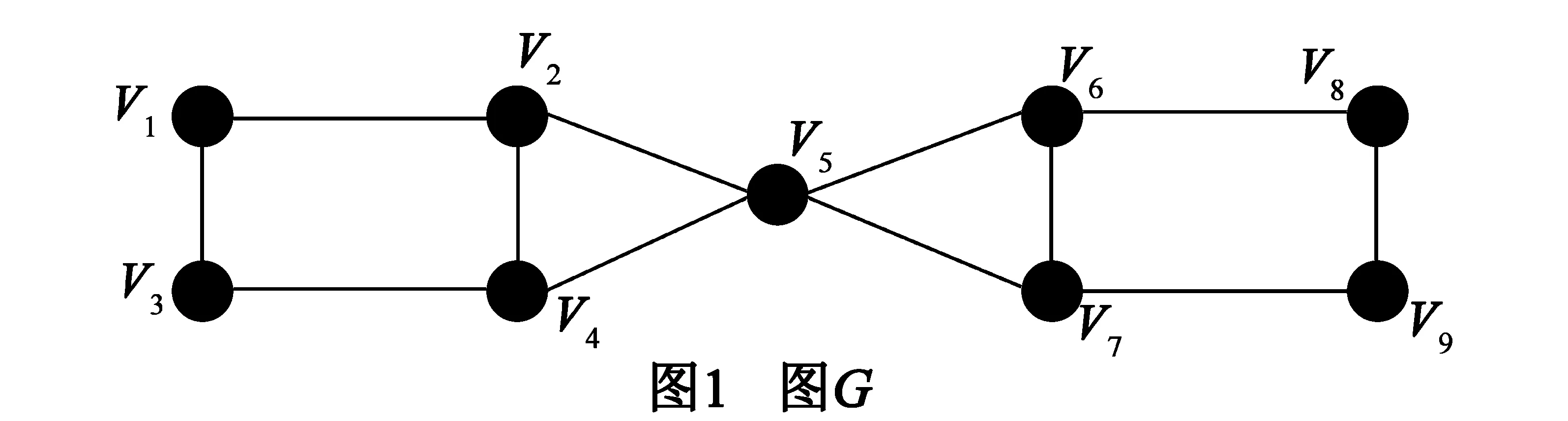
以一个具体的图为例，如图1所示，设G=(V，E)是无向图，V为顶点集，E为边集.其中第j条边用ej=(ej1,ej2)表示.

第一步，构造DNA纳米金颗粒共聚体.首先设计连接不同数目的寡核苷酸链的纳米晶体.DNA的末端通过巯基化的修饰可以连接到纳米金颗粒上，然后通过置换反应使金颗粒携带不同的DNA链.

经过退火反应，预先设计好的DNA纳米金颗粒的晶体可以生成代表图1的DNA纳米金颗粒共聚体，如图3所示.

第二步，删去顶点.删除顶点用DNA链置换反应技术来实现.例如以顶点V3为例，我们要删除已经形成的代表图G的三维纳米结构中的顶点V3，只要设计出能链置换与V3关联的2条边的DNA单链，这样在实验室条件下，在含有图G的三维纳米结构的溶液中加入取代链，经过DNA链置换反应，原来代表V3的DNA纳米金颗粒共聚体就被置换了，V3顶点就被成功地删除了.以此类推，图G的8个顶点都需要设计与其关联的边的取代链，根据链置换反应的条件，取代链与被取代链相比，应当含有相对较长的碱基互补序列，这是在设计和合成取代链时需考虑的问题.

在图1所示的图中要得到其连通度，删除顶点组合的数目将是28-2=254.解空间是比较大的，为缩小解空间可以参见不等式(3)，据此不等式删除的顶点将是不超过该图最小度δ(G)的任意几个顶点的组合而δ(G)=2,因此需删除顶点组合的数目，即可行解的数目将会缩小至

(4)

这样解空间可通过这一定理大大的缩小.删除顶点后形成的2种纳米结构组合中含有正确解.

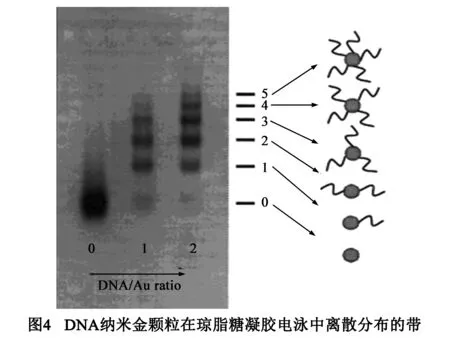
第三步，检测正确的解.这一步通过琼脂糖凝胶电泳技术进行.不同的DNA纳米金颗粒共聚体结构在琼脂糖凝胶电泳中呈现不同的形态，但仍然遵循电泳的一般规律，即颗粒的迁移率与其所带电荷和颗粒大小有关[25,26]，代表顶点的DNA纳米金颗粒共聚体根据其所连接的DNA单链的数目在电泳中可以区别，数目越多迁移率越小；代表图G的自组装结构由于含有最多的纳米金颗粒迁移率最小.如图4所示.利用DNA分子的特殊性质，我们可以控制连接的纳米颗粒的数目、大小、间距、空间维度和结构的柔性.金纳米颗粒具有大小和形状的均一性，并且在溶液中也便于操控，因此较为普遍地被用于各种研究.

3　算法及仿真结果分析

当删除顶点后，Gi代表删除i个顶点后的图形，detect(Gi)，如果恰好能使图Gi不连通，那么不连通的图结构在电泳中的分布可以通过对照区分出.如果连通，则令t=1；否则t=0.以本文图G为例，删除V5后得到两种不再连通的图结构，含有1个纳米金颗粒的自组装结构，在琼脂糖中很容易辨认出.

对于其它的图的连通度问题，本文提出的生物化学算法也是可行的.本算法的通用计算如下所示：

1for i1 to δ(G)

2delete(G，i)

3t=detect(Gi)

4if(t)

5returnκ(G)=i

6else goto1

7end

本文以顶点V3为例，通过Visual DSD仿真来验证该实验的可行性.表1是该仿真过程用到的序列，其中3和5段的基因序列长度是6bp和4bp，其他基因段均为20bp.为了方便以图5中所示的3种产物a，b，c表示.本文用NUPACK和Visual DSD对该实验仿真，该仿真实验能说明该实验的可行性.

在图6是顶点V3被链a，c置换反应过程.可以看出b链被a置换生成d和e，被c链置换生成f和g，同时e又可以被c置换，f可以被a置换,反应过程如图5所示，最后所有产物可能是d，e，f，h，g.

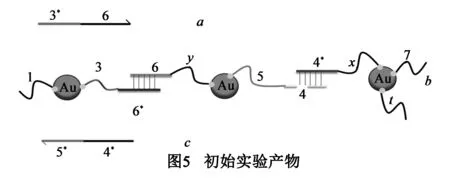
表1　实验仿真过程需要的DNA序列

名称序列(5’-3’)名称序列(5’-3’)1CCCAAAACAAAACAAAACAA5GCTA2CCCTTATCATATCAATACAAxCCCTATACTATACAATACTA3TATTCC7CCCTAATCTAATCATAACTA6CCCAAAACAAAACAAAACAAtCCCTAAACTTATCTAAACATyCCCTTAACTTAACAAATCTAaCCCTATTCAATTCAAATCAA

最后的反应产物与a和c浓度有关，浓度不同，产物也会不同.本文通过调整a，c的浓度进行对比分析.

本文通过对置换链a，c的浓度进行调整利用Visual DSD仿真，做出了在高浓度图7(a)，适中浓度图7(b)，低浓度图7(c)的3种情况的反应过程实验图，其中图7(a)是置换链a,c的浓度在6500nM，被置换链是5000nM.图7(b)是都在5000nM的情况，图7(c)是置换链a,c的浓度在4500nM，被置换链是5000nM.通过对比图7(a)，图7 (b)我们可以看出图7(a)参加反应的收敛速度明显要高于图7(b) 图6(c)，图7(a)在500s的时候基本开始收敛，在1400s的时候已经稳定并且收敛后反应也比较充分，杂质比较少；而图7(b)和图7(c)都是在700s的时候才开始收敛，在2100s时才趋于稳定并且收敛后反应产物比较复杂，对于顶点V1来说相当于删掉的情况浓度比较小.在7(a)高浓度图，图7(b)适中浓度，图7(c)低浓度这3种情况下最后的反应产物如表2.

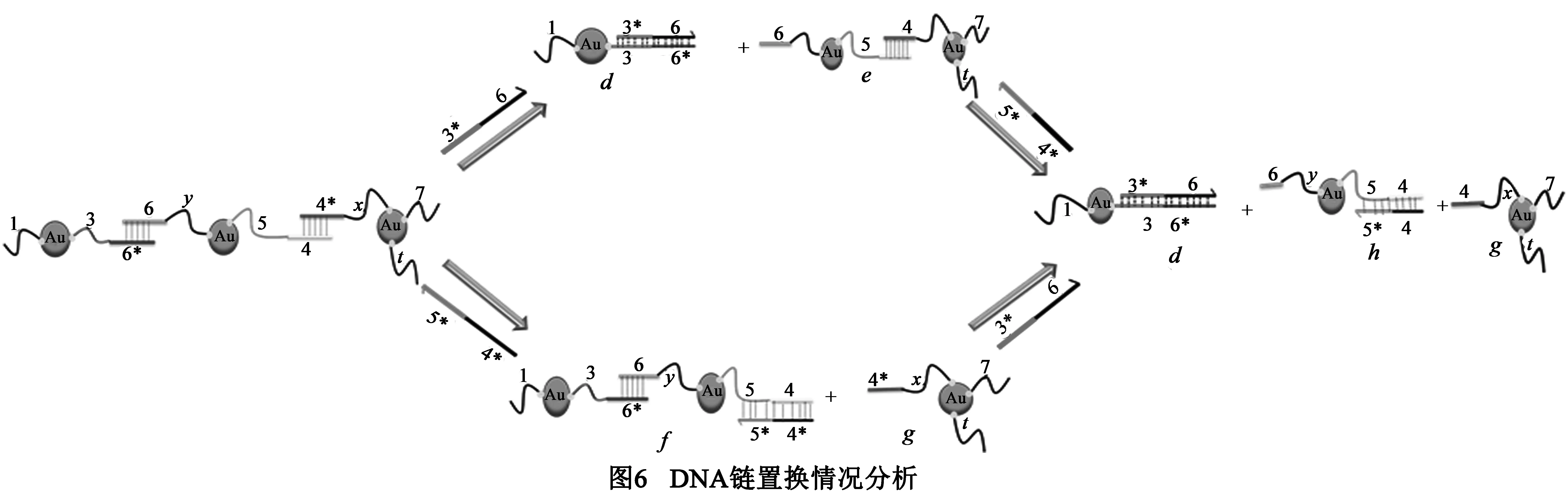
表2在高浓度(a)，适中浓度(b)，低浓度(c)3种情况下的浓度分析

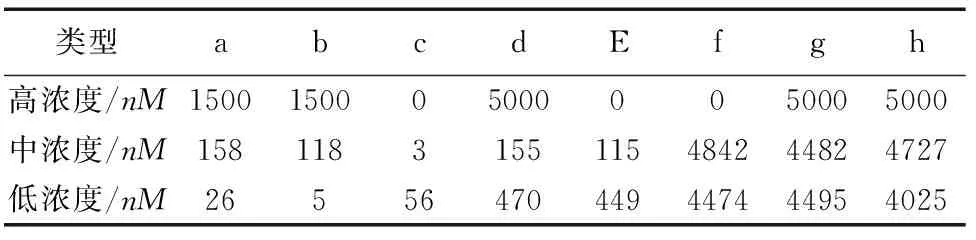
类型abcdEfgh高浓度/nM15001500050000050005000中浓度/nM1581183155115484244824727低浓度/nM26556470449447444954025

本文最后利用退火反应、链置换反应、琼脂糖凝胶电泳技术，通过这些生物化学技术对最后反应产物进行操作，然后再通过测序就可以验证图1的连通度,具体操作过程:构建DNA逻辑计算模型时，按照仿真的中图7(a)的比例进行实际实验操作.将混合液体置于常温下进行退火.此步骤后，可进行琼脂糖凝胶电泳进行检测.实验中，DNA链置换在缓冲液中实现.加入的DNA链和运算逻辑模块混合后，在室温下反应6h以上，即可进行PAGE电泳结果检测.

4　讨论

假设图的顶点个数为n，边的条数为m，那么本文提出了一种利用DNA纳米金颗粒共聚体的自组装过程解决连通度问题的DNA计算方法，构建了解决图的连通度问题的三维DNA自组装计算模型的时间复杂度O(n+m).而1991年，kanevsky & Ramachandram提到当顶点个数k=4的时间复杂度为O(n2)；1996年Henzinger & Rao提到当顶点个数k=k时间复杂度为O(kmnlogn).本文的算法设计大大的缩小了时间复杂度.另外本文提出的生物化学算法分别使用了退火反应、链置换反应、琼脂糖凝胶电泳技术，这些生物化学技术都便于操作；设计和合成DNA纳米金颗粒共聚体的化学方法也是简便易行的.该计算模型的优势还在于利用了DNA分子碱基序列的可编程性，以及纳米颗粒的特殊化学结构和性质，与传统DNA计算方法相比，不仅降低了实验的繁琐程度，而且也克服了随着问题规模的增加带来的“指数爆炸问题”，降低了计算复杂度.基于DNA纳米颗粒共聚体的特殊性质，其它的检测技术如透射电镜技术，荧光技术也能很好地用于检验本文提出的计算模型，这为下一步DNA自组装计算模型的应用提供了可行的方案.

本文提出的解决图的连通度问题的三维DNA自组装计算模型虽然是理论模型，但是通过Visual DSD的仿真验证了该实验的可行性并且通过调整置换链的浓度的对比分析，说明在实际实验中要将置换链过量这样更能增加实验成功概率.尽管如此，在实际的操作和实验中，仍然无法避免非解的产生，许多无法预料的问题仍然是实验过程中无法控制的因素.在实验中不断完善和检验理论模型，在新的技术和方法中改进理论模型和实验方法，这是建立通用的DNA计算模型的有效途径.

[1]Adleman L.Molecular computation of solution to combinatorial problems[J].Science,1994,66:1021-1024.

[2]Lipton R J.Using DNA to solve NP-complete problems[J].Science,1995,268:542-545.

[3]Ouyang Q,Kaplan P D,Liu S,et al.DNA solution of the maximal clique problem[J].Science,1997,278:446-449.

[4]杨静,张成,许进,等.基于环形DNA分子的一种求解最大集团的计算模型[J].中国科学,2010,40(8):1078-1085.

Yang Jing,Zhang Cheng,Xu Jin,et al.A novel computing model of the maximum clique problem based on circular DNA[J].SCIENCE CHINA Information Sciences,2010,40(8):1078-1085.(in Chinese)

[5]张成，马丽娜，董亚非等.自组装DNA链置换分子逻辑计算模型[J].科学通报，2012，31(57)：2909-2915.

Zhang Cheng,Ma Lina,Dong Yafei,et al.A computing model of self-assembly based on DNA strand displacement[J].Chinese Science Bulletin,2012,31(57):2909-2915.(in Chinese)

[6]Faulhammer D,Cukras A,Lipton R J,et al.Molecular computation:RNA solutions to chess problems[J].P Natl AcadSci,2000,97:1385-1389.

[7]Head T,Rozenberg G,Bladergroen R S,et al.Computing with DNA by operating on plasmids[J].BioSystems,2000,57:87-93.

[8]Mao CD,LaBean T H,Reif J H,et al.Logical computation using algorithmic self-assembly of DNA triple-crossover molecules[J].Nature,2000,407:493-496.

[9]Carbone A,Seeman N C.Circuits and programmable self-assembling DNA structures[J].P Natl Acad Sci,2002,99:12577-12582.

[10]Brun Y.Arithmetic computation in the tile assembly model:addition and multiplication[J].Theor Comput Sci,2007,378:17-31.

[11]Sharma J,Chhabra R,Cheng A,Brownell J,Liu Y,Yan H.Control of self-assembly of DNA tubules through integration of gold nanoparticles[J].Science,2009,313:112-116.

[12]Mastroianni AJ,Claridge SA,Alivisatos AP.Pyramidal and chiral groupings of gold nanocrystals assembled using DNA scaffolds[J].JAm Chem Soc 2009,131:8455-8459.

[13]杨玉星，王世英.Ménage问题的一种粘贴DNA算法[J].电子学报，2012，40(4):751-755.

Yang Yuxing,Wang Shiying.A DNA sticker algorithm for the ménage problem[J].Acta Electronica Sinica,2012,40(4):751-755.(in Chinese)

[14]吴帆,李肯立.基于自组装的N皇后问题DNA计算算法[J].电子学报，2013，41(11)：2174-2180.

Wu Fan,Li Kenli.An algorithmin tile assembly model for N queen problem[J].Acta Electronica Sinica,2013,41(11):2174-2180.(in Chinese)

[15]Zhang C,Yang J,Xu J.Circular DNA logic gates with strand displacement[J].Langmuir,2010,26,1416-1419.

[16]Qian L L,Winfree E.Scaling up digital circuit computation with DNA strand displacement cascades[J].Science,2011,332(3):1196-1201.

[17]Cheng Z,Jing Y,Jin X.Molecular logic computing model based on self-assembly of DNA nanoparticles[J].Chinese Science Bulletin,2011,56(33):3566-3571.

[18]Jing Yang,Lingjing Shen,et al.Fluorescent nanoparticle beacon for logic gate operation regulated by strand displacement[J].ACS Appl Mater Interfaces,2013,5:5392-5396.

[19]Zhang C,Ma J J,Yang J,Dong Y F,Xu J.Control of gold nanoparticles based on circular DNA strand displacement[J].Journal of Colloid and Interface Science,2014,418:31-36.

[20]Bondy J A,Murty U S R.Graph Theory with Applications[M].London,The Macmillan Press L T D,1976,108-117.

[21]王树禾.图论[ M ].北京:科学出版社,2004:141-144.

Wang Shuhe.Graph Theory[M].Beijing:Sciences Press,2004:141-144.(in Chinese)

[22]马润年,张强，高琳,等.图的最大权团的DNA计算[J].电子学报，2004，32(1):13-16.

Ma Runnian,Zhangqiang,Gao Lin.et al.Using DNA to solve the maximum weight clique of graphs[J].Acta Electronica Sinica,2004,32(1):13-16.(in Chinese)

[23]方刚,张社民,许进.边连通度问题的三维DNA图结构解法[J].系统工程与电子技术，2006，28(1):119-121.

Fang Gang,Zhang Shemin,Xu Jin.Three dimensional DNA graph structure solution to edge-connectivity[J].Systems Engineering and Electronics,2006,28(1):119-121.(in Chinese)

[24]张社民,方刚.连通度问题的三维DNA结构进化算法[J].计算机工程与应用，2007，43(7):41-44.

Zhang Shemin,Fang Gang.Three dimensional DNA structure solution to connectivity based on evolutionary algorithm[J].Computer Engineering and Applications,2007,43(7):41-44.(in Chinese)

[25]Daniela Zanchet,Christine M Micheel,Wolfgang J Parak,Daniele Gerion,A Paul Alivisatos.Electrophoretic isolation of discrete Au nanocrystal/DNA conjugates[J].Nanoletters,2001,1(1):32-35.

[26]Daniela Z,Christine M,Wolfgang P,A Paul Alivisatos.Electrophoretic and structural studies of DNA-directed Au nanoparticle groupings[J].J Phys Chem B,2002,106:11758-11763.

王艳钗女,1989年10月出生，河南清丰人,2012年毕业于河南师范大学计算机与信息学院.2012年进入陕西师范大学计算机科学学院.从事DNA计算和基因网络方面的有关研究.

E-mail:wangyanchai1025@163.com

董亚非男,1963年12月出生，陕西西安人,副教授、硕士生导师、中国系统工程学会会员、IEEE会员.华中科技大学工学博士，生物医学博士后.现为陕西师范大学副教授，主要从事DNA计算、基因网络及生物信息学等方面的研究工作.

E-mail:dongyf@snnu.edu.cn

The Application of DNA/ Nanoparticle Conjugate on the Graph’s Connectivity Problem

WANG Yan-chai1,ZHANG Hui2,DONG Ya-fei1,2

(1.College of Computer Sciences,Shaanxi Normal University,Xi′an,Shaanxi 710119,China; 2.College of Life Sciences,Shaanxi Normal University,Xi′an,Shaanxi 710119,China)

A DNA computing algorithm is proposed in this paper which uses the assembly process of DNA/Au nanoparticle conjugate to solve an NP-complete problem in the Graph theory,the connectivity problem,and a 3D DNA self-assembly algorithm model is also established.According to the algorithm,we need to design the special DNA/Au nanoparticle conjugate which will be based on a specific graph.Then,a series of experiments are performed to get the final answer and Visual DSD is used as the simulation in the paper,which will provide a practical way to the best use of DNA self-assembly algorithm model.

DNA computing;DNA/Au nanoparticle;graph’s connectivity;3D model

2013-12-26;

2014-10-24；责任编辑：郭游

国家自然科学基金(No.61272246);陕西师范大学2013年勤助科研创新基金(No.QZZD13005);陕西师范大学重点项目和陕西师范大学研究生培养创新基金

TN911

A

0372-2112 (2016)07-1561-06

��学报URL:http://www.ejournal.org.cn

10.3969/j.issn.0372-2112.2016.07.006