HAN基液体推进剂喷雾场液滴尺寸分布的简化模型
2016-07-15余永刚
王 婕, 余永刚,刘 焜,2
(1.南京理工大学能源与动力工程学院,江苏 南京 210094;2.上海船用柴油机研究所,上海 201213)
HAN基液体推进剂喷雾场液滴尺寸分布的简化模型
王婕1, 余永刚1,刘焜1,2
(1.南京理工大学能源与动力工程学院,江苏 南京 210094;2.上海船用柴油机研究所,上海 201213)
摘要:为了建立HAN基液体推进剂喷雾场液滴尺寸分布的简化模型,基于最大熵原理,在质量守恒与概率和为定值的约束条件下,用拉格朗日因子法则推导了液滴尺寸分布函数,将该函数应用于HAN基液体推进剂模拟工质喷雾场液滴尺寸的预估;采用相位多普勒粒子动态分析仪(PDA)测量了HAN基液体推进剂模拟工质在1.8~2.6MPa喷射压力下对撞式喷嘴雾化液滴尺寸分布;通过最小二乘法优化Nukiyama-Tanasawa分布函数式中的q值对数目微分分布进行了修正,拟合得到q值与喷射压力p之间的函数关系为q(p)=-0.344p2+1.525p+1.268。结果表明,计算得出的液滴尺寸数目微分分布与HAN基液体推进剂喷雾场实测数据变化趋势相符,表明建立的液滴尺寸分布模型是合理的。
关键词:HAN基液体推进剂;最大熵原理;液滴尺寸分布;对撞式喷嘴;喷射压力;最小二乘法
引 言
喷射雾化在动力机械与工程领域的燃气轮机、气体燃料发动机、飞机和火箭发动机中都起着重要作用[1]。HAN基液体推进剂被美国NASA、欧洲航天机构等认定为最具潜力的一种液体推进剂,具有比冲高、密度高、无毒、贮存安全等优点,是新一代绿色液体火箭发动机的理想燃料[2]。液滴粒径和液滴粒径分布是衡量喷嘴雾化质量的重要参数,对喷雾系统的设计优化有指导作用。
Babinsky和Sojka[3]总结出3种预测液滴粒径分布的方法:最大熵方法、经验法和离散概率函数法。Jaynes[4]在1957年提出信息熵理论中最著名的最大熵原理。Li等[5]提出最大熵法则只适用于孤立的热力学平衡系统,而实际雾化过程并非如此,所以以最大熵法则为基础得出的液滴粒径分布与不同的实验数据相比时有不同程度的差异。曹建明[6-7]运用最大熵原理推导了 Nukiyama-Tanasawa型喷雾液滴尺寸分布函数的具体形式。黄兵等[8]在最大熵/熵增原理基础上发展有较好收敛特性的数值计算方法。李巧红等[9]针对气流速度一定的气流式喷嘴,在最大熵理论的基础上研究了不同液气质量比对液滴粒径分布的影响。Nath等[10]基于最大熵方法对平面射流破碎形成的液滴尺寸分布和速度分布进行了预测。Movahednejad等[11]用最大熵原理预测了液滴初级破碎区域的液滴直径分布。刘妍卿等[12]将最大熵模型应用于可调式机械-空气喷嘴雾化中,计算得出的累计体积分布以及体积分布结果都与实验结果相符。郭金海等[13]通过实验测得不同液体流量下压力旋流喷嘴雾化液滴粒径分布,在平均粒径的约束条件下用三参数最大熵模型对雾化液滴粒径进行预测。
本研究在最大熵模型的基础上,在质量守恒与概率和为定值的约束条件下,推导出液滴数目分布函数,并与喷雾场实测数据进行了比较,以期为HAN基液体推进剂喷雾场液滴尺寸分布的研究提供参考。
1液滴尺寸分布函数的推导
在物理和工程应用中,信息熵表达形式为
(1)
式中:S为信息熵;K为常数;Pi为某一直径下液滴数目的概率。
当信息熵最大时,可以得到机率最大的分布函数,此时有

(2)
由质量守恒可知,单位时间内产生的所有液滴质量之和等于喷雾的质量流量。则可得
(3)

另一约束条件为
(4)
使用拉格朗日因子法,得到函数F如下
(5)

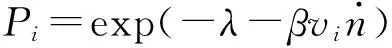
(6)
式中:λ与β为拉格朗日因子。
把式(6)带入式(4),得

(7)
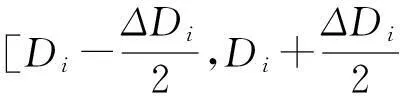
(8)
(9)
又因为假定液滴粒径是连续变量,则式(7)可转换为

(10)
对式(10)积分,得
(11)
假设Dmin=0,Dmax=∞,则有
(12)
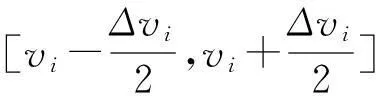
(13)
由式(13)可得
(14)
把式(12)带入(14),可得

(15)
将式(15)与Nukiyama-Tanasawa分布函数(式(16))进行比较
(16)
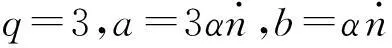
2实验
2.1实验装置
为了研究HAN基液体推进剂对撞射流在大气环境中的喷雾特性,设计的喷雾实验装置示意图如图1所示。
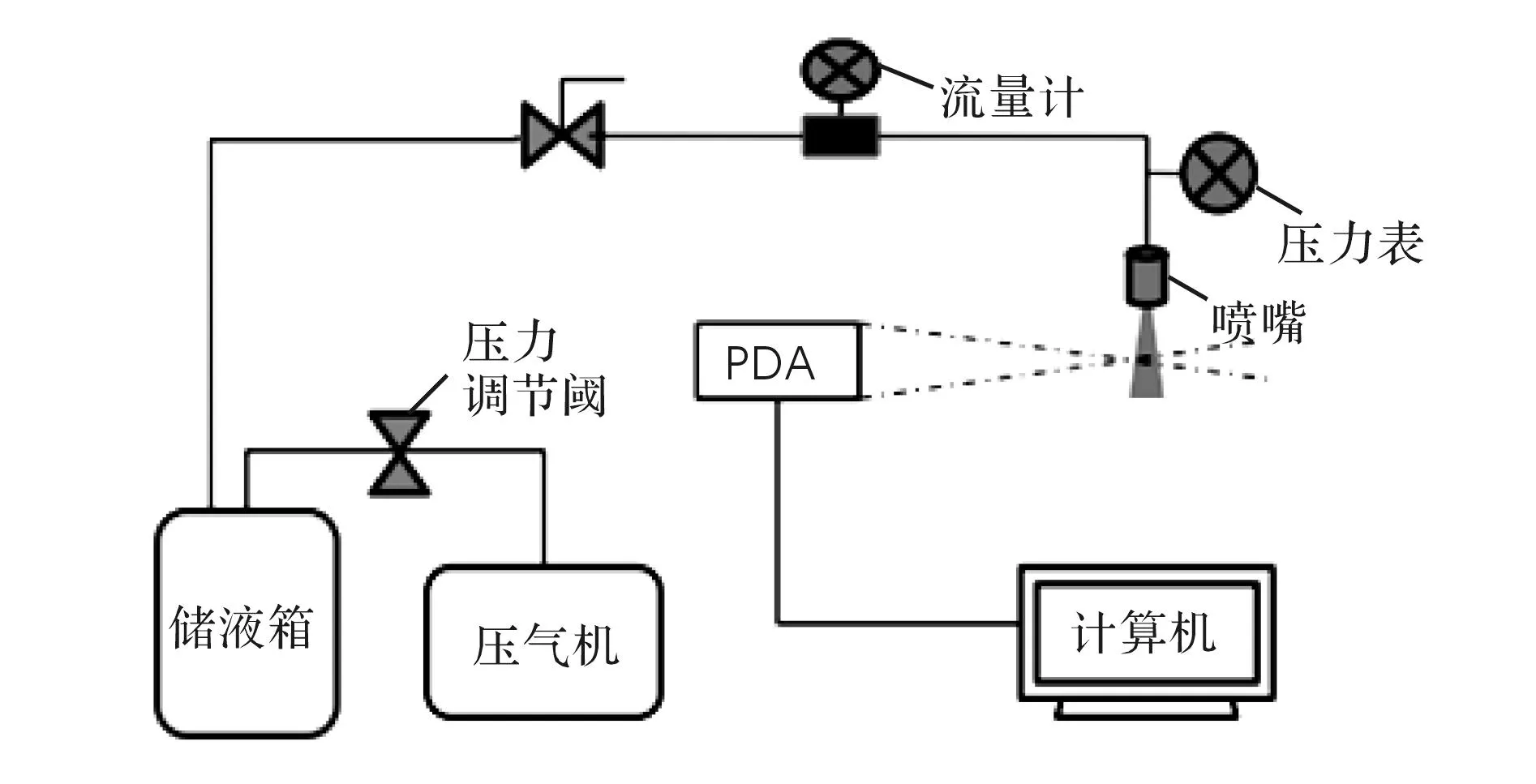
图1 喷雾实验装置示意图Fig.1 Schematic diagram of the spray test setup
由图1可以看出,喷雾实验装置由压气机、储液箱、流量计、压力表、PDA、喷嘴等组成。采用HAN基液体推进剂模拟工质进行实验,模拟工质密度为1300kg/m3,黏度为1.2×10-3Pa·s。实验采用的PDA测试系统粒径测量范围为0.5~200μm,测量精度在1%以内;速度测量范围为-300~1000m/s,测量精度在0.1%以内。
2.2实验过程
实验过程中,高压气源提供喷射压力,液体模拟工质贮存在图1中的储液箱内。实验时,提前打开液体阀门,调节喷嘴前压力到实验要求值。雾化过程稳定后,对PDA实验系统进行手动调焦,使测量原点处于喷嘴出口中心处,随后在PDA系统配套的BSAFlow软件中设置测量点坐标,系统可自动采集所需雾化液滴数据。
3结果与讨论
3.1喷雾场液滴尺寸分布
在喷嘴压降分别为1.8、2.2和2.6MPa工况下,液滴平均直径D10的数目分布图如图2所示,其中纵坐标P为液滴数目所占百分比。

图2 液滴平均直径的数目分布Fig.2 Number distribution of average diameter of droplets
由图2可以看出,随着喷嘴压降的增加,液滴平均直径往小粒径方向发展,这是由于喷嘴压降增加时,撞击射流的动量增大,使环境中空气扰动作用增强,液滴与空气之间的作用力也增大,液滴更容易发生二次破碎,从而使得液滴粒径减小。
3.2模拟计算结果与实验结果的比较
将采用式(15)得到的计算结果与对撞式喷嘴在大气环境中无量纲化的实验结果进行比较。通过最小二乘法来优化q值,使得实验数据与其对应的计算结果间的标准差最小时,q值即为所取。计算结果与实验数据的比较如图3所示,图中黑三角点代表各喷嘴压降下实验测得数据,实线为Nukiyama-Tanasawa分布函数在实验数据与计算结果间标准差最小时所取q值计算得出的分布曲线,虚线为当q=3时计算得到的理论分布曲线。
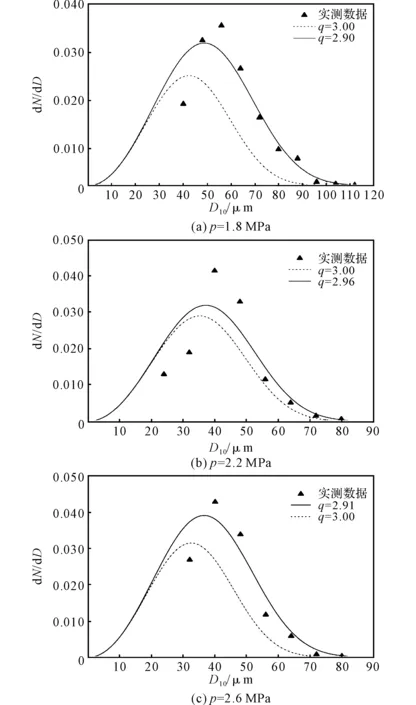
图3 数目微分分布理论计算与实测数据的对比曲线Fig.3 Comparison curves of the droplet size differentialnumber distribution and the experimental data
由图3可知,通过适当减小q值,计算得出的峰值偏向较大液滴直径的范围,同时也大于q=3时计算得出的峰值,与实验峰值点更接近。通过改变q值可以对数目微分分布进行修正。其中,q值与喷射压力(p)之间存在某种函数关系,通过数值拟合得到q与p之间的二次函数关系如下
q(p)=-0.344p2+1.525p+1.268
(17)
所以,式(16)中q也可替换为式(17)中的q(p),q(p)拟合曲线如图4所示。

图4 q值与喷射压力之间的关系曲线Fig.4 The relationship curve between q andinjection pressure
由图4可知,通过拟合得到了q(p)与喷射压力之间的二次函数图像,当喷射压力为2.2MPa时,q(p)取最大值2.96。
综上所述,以最大熵原理为基础计算得出的液滴数目微分理论分布与HAN液体推进剂模拟工质喷雾场的实验数据变化趋势基本相同,仅实验峰值稍大,液滴数目微分分布满足最大熵原理,说明建立的液滴尺寸分布模型是合理的。
4结论
(1)在最大熵原理的基础上,利用拉格朗日因子法推导出液滴数目微分分布函数。
(2)通过优化q值可对数目微分分布进行修正,q值与喷射压力之间满足二次函数关系q(p)=-0.344p2+1.525p+1.268。
(3)计算得出的液滴数目微分分布与HAN基液体推进剂模拟工质喷雾场液滴的实测数据变化趋势相符,表明该模型是合理的。
参考文献:
[1]田春霞, 仇性启, 崔运静. 喷嘴雾化技术进展[J]. 工业加热, 2005, 34(4):40-43.
TIAN Chun-xia, QIU Xing-qi, CUI Yun-jing. Development of technology on atomization[J]. Industrial heating, 2005, 34(4):40-43.
[2]贺芳, 方涛, 李亚裕, 等. 新型绿色液体推进剂研究进展[J]. 火炸药学报, 2006, 29(4): 54-57.
HE Fang, FANG Tao, LI Ya-yu, et al. Development of green liquid propellants[J]. Chinese Journal of Explosives & Propellants(Huozhayao Xuebao), 2006, 29(4): 54-57.
[3]Babinsky E, Sojka P E. Modeling drop size distributions[J]. Progress in Energy and Combustion Science, 2002, 28(4): 303-329.
[4]Jaynes E T. Information theory and statistical mechanics[J]. Physical Review, 1957, 106(4): 620-630.
[5]Li X G, Li M S, Fu H J. Modeling the initial droplet size distribution in sprays based on the maximization of entropy generation[J]. Atomization and Sprays, 2005, 15(3): 295-321.
[6]曹建明. Nukiyama-Tanasawa型雾化液滴尺寸分布函数的引申[J]. 中国公路学报, 1999(12):106-111.
CAO Jian-ming. An extension of the Nukiyama-Tanasawa droplet size distribution function in sprays [J]. China Journal of Highway and Transport, 1999(12):106-111.
[7]曹建明. 雾化液滴尺寸和速度分布函数的推导[J]. 交通运输工程学报, 2007, 7(1):34-36.CAO Jian-ming. Derivation on droplet size and velocity distribution functions in atomization[J]. Journal of Traffic Transportation Engineering, 2007, 7(1):34-36.
[8]黄兵, 张楠. 液体火箭发动机初始雾化液滴分布预测[J]. 火箭推进, 2007, 33(2): 31-39.
HUANG Bing, ZHANG Nan. Prediction of droplet size distributions of primary atomization in liquid rocket engine[J]. Journal of Rocket Propulsion, 2007, 33(2): 31-39.
[9]李巧红,刘海峰, 李伟锋, 等. 最大熵原理预测气流式喷嘴雾化液滴粒径分布[J]. 华东理工大学学报(自然科学版), 2009, 35(01): 25-29.
LI Qiao-hong, LIU Hai-feng, LI Wei-feng, et al. Prediction of droplet size distribution in spray of air-blast nozzle using maximum entropy principle[J]. Journal of East China University of Science and Technology (Nature science edition) , 2009, 35(1): 25-29.
[10]Nath S, Datta A, Mukhopadyay A, et al. Prediction of size and velocity distributions in sprays formed by the break up of planar liquid sheets using maximum entropy formalism[J]. Atomization and Sprays, 2011, 21(6):483-501.
[11]Movahednejad E, Ommi F, Hosseinalipour S M. Application of maximum entropy method for droplet size distribution prediction using instability analysis of liquid sheet[J]. Heat and Mass Transfer, 2011, 47(12): 1591-1600.
[12]刘妍卿, 仇性启,王超. 可调式喷嘴雾化液滴粒径分布预测[J]. 工业加热, 2012, 41(4):31-34.
LIU Yan-qing, QIU Xing-qi, WANG Chao. Prediction of droplet size distribution in adjustable nozzle[J]. Industrial Heating, 2012, 41(4):31-34.
[13]郭金海, 谭心舜, 毕容天, 等. 压力旋流喷嘴雾化滴径分布的模型预测和实验[J]. 化工进展, 2012, 31(3): 528-532.
GUO Jin-hai, TAN Xin-shun, BI Rong-tian. Model prediction and experiment study on spray droplet size distribution of pressure swirl nozzle[J]. Chemistry Industry and Engineering Progress, 2012, 31(3): 528-532.
Simplified Model on Droplet Size Distribution in the Spray Field of HAN-based Liquid Propellant
WANG Jie1, YU Yong-gang1, LIU Kun1,2
(1.School of Energy and Power Engineering, Nanjing University of Science and Technology, Nanjing 210094, China;2.Shanghai Marine Diesel Engine Research Institute, Shanghai 201213, China)
Abstract:To establish the simplified model of the droplet size distribution in the spray field of HAN-based liquid propellant, based on maximum entropy principle, the droplet size distribution function was derived by using Lagrange method under the conditions of mass conservation and that the sum of probability is the fixed value, this function was used to predict the droplet size distribution of HAN-based liquid propellant simulation medium spray field. A phase Doppler particle dynamic analyzer (PDA) was used to measure the droplet size distribution in the spray field of impinging nozzle with HAN-based liquid propellant simulation medium under the injection pressure of 1.8MPa to 2.6MPa. The differential number distribution was revised by using least squares method to optimize the value ofqin Nukiyama-Tanasawa distribution function formula, the function relationship betweenqand injection pressurepobtained by fitting wasq(p)=-0.344p2+1.525p+1.268. The results show that the changing trend of the calculated droplet size differential number distribution agrees well with experimental data of the HAN-based liquid propellant,indicating that the droplet size distribution model established is reasonable.
Keywords:HAN-based liquid propellant;maximum entropy principle;droplet size distribution;impinging nozzle;injection pressure;least squares method
DOI:10.14077/j.issn.1007-7812.2016.03.017
收稿日期:2016-01-25;修回日期:2016-03-18
基金项目:教育部博士点基金资助项目(20113219110024)
作者简介:王婕(1992-),女,硕士研究生,从事含能材料的雾化研究。E-mail:13770831835@163.com
中图分类号:TJ55;V434
文献标志码:A
文章编号:1007-7812(2016)03-0084-05
