基于车辆运动约束的里程计误差在线标定方法

李 艳，杨 波，薛 亮，周小刚

（1. 长安大学 信息学院，西安 710064；2. 第二炮兵工程大学 控制工程系，西安 710025）

基于车辆运动约束的里程计误差在线标定方法

李 艳1，杨 波2，薛 亮2，周小刚2

（1. 长安大学 信息学院，西安 710064；2. 第二炮兵工程大学 控制工程系，西安 710025）

为了降低里程计误差对捷联惯导/里程计组合定位定向精度的影响，提出了基于车辆运动约束条件的里程计误差在线标定方法。通过对里程计标度因数误差进行建模，推导建立了航位推算的误差模型，将航位推算的速度输出沿车体横向、垂向的投影作为量测的一部分，将捷联惯导输出的速度、位置信息与航位推算输出的对应信息相减作为另一部分量测，通过卡尔曼滤波获得里程计标度因数误差等状态量的最优估计值，实现里程计误差的在线标定。仿真结果表明，该方法能够有效地标定出里程计标度因数误差，从而确保了捷联惯导/里程计组合定位定向的精度。

里程计误差标定；车辆运动约束；组合定位定向；航位推算；卡尔曼滤波

为了实现发射车、装甲车等特殊军用车辆的高精度自主定位定向，特别是具备较强的抗干扰能力，国内外广泛研究了车载捷联惯导/里程计组合定位定向技术[1-4]。现有的研究结果表明[4-6]，里程计标度因数误差对组合定位定向精度会造成较大影响，而且在不同的导航任务中标度因数可能不同，即使在同一次任务中轮胎状态的变化也会使标度因数发生变化。为此，必须设法对里程计的标度因数误差进行有效的在线标定。

文献[6]利用差分 GPS 的高精度定位特性，结合捷联惯导和里程计的输出，利用卡尔曼滤波对里程计标度因数变化进行标定，但是GPS的引入必将带来抗干扰性和自主性问题；文献[7]研究了基于递推最小二乘的标定方法，利用跑车过程中 GPS 提供的位置信息对里程计标度因数进行标定，同样存在引入GPS的问题；文献[4][8]对里程计标度因数进行建模并列入系统状态，利用惯导与里程计的速度输出构造量测，取得了较高的组合导航精度，但是位置误差终究缓慢发散。

为此，本文提出一种基于车辆运动约束条件的里程计误差在线标定方法。首先对里程计标度因数误差进行建模，推导建立航位推算的误差模型；然后，不仅利用捷联惯导与航位推算速度、位置输出构造量测，而且将航位推算的速度输出沿车体横向与垂向上的投影引入量测，利用卡尔曼滤波对里程计标度因数误差进行估计，从而不仅实现里程计误差的在线标定，而且有效提高捷联惯导/里程计组合定位定向的精度。

1 里程计误差在线标定方案

在捷联惯导/里程计组合定位定向系统中，捷联惯导系统输出载车的姿态、速度和位置信息，里程计输出载车行驶的路程增量。首先，利用捷联惯导输出的载车姿态矩阵与里程计输出的路程增量进行航位推算解算，实时获得载车速度和位置信息；然后，将捷联惯导输出的速度、位置信息与航位推算输出的对应信息相减作为量测之一，将航位推算的速度输出沿车体横向与垂向上的投影作为量测之二，送入捷联惯导/里程计组合定位定向滤波器中进行滤波；经过滤波计算获得捷联惯导误差、里程计误差的最优估计值，从而实现对里程计误差的在线标定，而惯导系统误差估计值则被用来对捷联惯导进行误差修正，并将修正后惯导系统输出作为整个组合定位定向系统的输出，其中，捷联惯导与航位推算均采用东北天地理坐标系作为导航坐标系。里程计误差的在线标定原理如图1所示。

2 航位推算的误差模型

在图 1所示的捷联惯导/里程计组合定位定向系统中，航位推算的误差源主要来自捷联惯导数学平台姿态误差以及里程计测量误差，其中前者在很多文献中已有研究，故本文重点考虑里程计的测量误差。

2.1 里程计的误差模型

里程计的测量误差一般包括标度因数误差和安装误差[9]。其中，安装误差可通过实验标定而得到有效补偿，而标度因数误差则主要与轮胎气压、温度、磨损情况以及路面状况等因素有关[8,10]，因此无法通过实验事先标定来准确确定，为此需要对其进行分析建模。

里程计的标度因数误差取决于车辆行驶过程中轮胎气压、温度、磨损情况等因素，一般情况下在每次行驶过程中里程计的标度因数误差基本保持在某一随机常值上，因此里程计的标度因数误差满足

2.2 航位推算的速度误差方程

由于捷联惯导数学平台姿态误差以及里程计测量误差的存在，导致航位推算获得的速度和位置信息必然存在一定的误差，而且这些误差随着递推解算在不断累积。为此，需要对它们进行分析与建模。

在航位推算过程中，由于里程计标度因数误差δKD的存在，载车沿车体正前方向上速度的测量值和真实值vD之间存在如下关系：

将式(5)代入到式(6)中，展开并忽略关于误差的二阶小量可得：

图1 里程计误差的在线标定原理框图Fig.1 Schematic of online calibration for odometer’s errors

2.3 航位推算的位置误差方程

设航位推算的纬度、经度、高度误差分别为δLD、δλD、δhD，则根据地理系下位置解算微分方程可知航位推算实际输出的位置应满足下列方程：

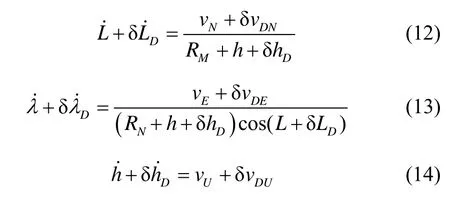
展开式(12)～(14)并略去关于误差的二阶小量，再与地理系下位置解算微分方程相比较，可以获得航位推算的位置误差方程如下：

将式(9)～(11)代入到式(15)～(17)中可得：

3 基于车辆运动约束的里程计误差在线标定算法

为了对里程计误差进行在线标定，需要将捷联惯导与航位推算误差一起作为组合定位定向的系统状态，即系统状态X包括捷联惯导数学平台姿态误差φE、φN、φU，速度误差δvE、δvN、δvU，位置误差δL、δλ、δh，陀螺常值漂移 εbx、εby、εbz，加速度计常值偏置∇bx、∇by、∇bz，航位推算的位置误差δLD、δλD、δhD，里程计标度因数误差δK。其中，航位推算的速度误差与捷联惯导数学平台姿态误差、里程计标度因数误差之间存在线性关系，因此不再列入系统状态。从而，根据捷联惯导与航位推算的误差模型，可以列写出组合定位定向的状态方程，对此文中不再赘述。

将捷联惯导输出的载车速度、位置信息与航位推算输出的对应信息相减作为量测之一，即

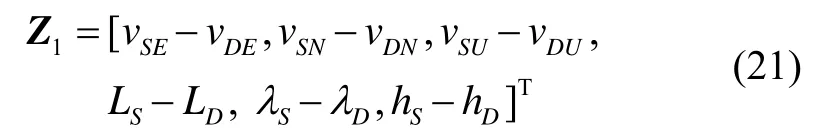
式中：vSE、vSN、vSU为捷联惯导输出的载车东、北、天向速度，vDE、vDN、vDU为航位推算输出的对应速度，LS、λS、 hS为捷联惯导输出的纬度、经度、高度，LD、λD、hD为航位推算输出的对应位置。

由于捷联惯导与航位推算输出的速度、位置信息中均含有误差，因此根据式(21)有：

再将式(9)～(11)代入到式(22)中可得：

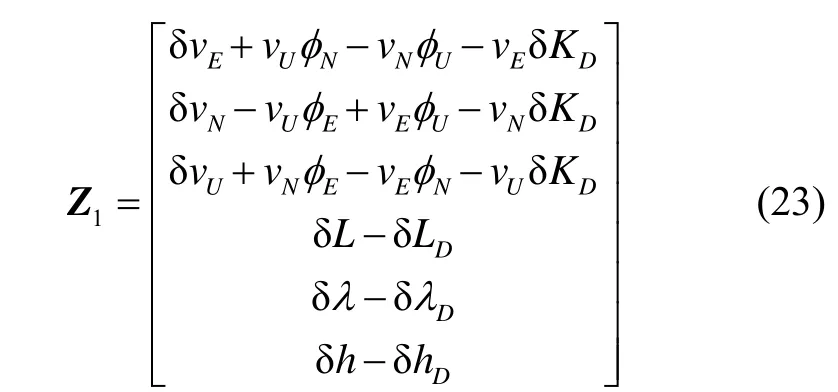
对于在道路上正常行驶的车辆，其满足如下运动学约束：如果车辆不发生侧滑和跳跃，则其行驶速度沿车体横向、垂向上的分量应该为零[11]。基于这一运动约束条件，可以将航位推算的速度输出沿车体坐标系x、z轴上的投影作为量测之二，即

由于系统误差的存在，导致航位推算的实际速度输出沿车体系x、z轴上的投影并不为零，而是存在一定的误差。设沿车体系 x、z轴上投影的误差分别为δvx、δvz，则根据式(24)可知：

式中：Tij(i,j=1,2,3)为姿态矩阵的第i行、第j列元素。

载车速度理论值Vn与其在车体系下的投影Vb之间则满足：

将式(28)展开，并取第一、三行可得：

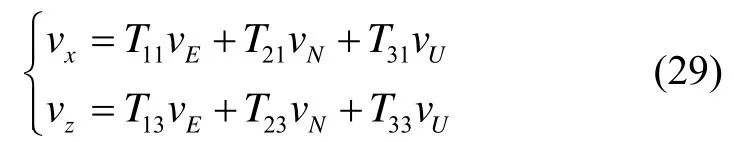
于是，将式(27)展开取第一、三行，并将其与式(29)进行比较可得：

再将式(9)～(11)代入到式(30)中可得：

从而，将量测Z1、Z2一起作为组合定位定向的量测，并根据式(23)(25)和(31)可将组合定位定向的量测方程表达为如下形式：

建立状态方程与量测方程以后，利用卡尔曼滤波就可以计算获得系统状态X（包含里程计标度因数误差）的最优估计值，从而实现对里程计误差的在线标定，并利用所获得的惯导系统误差估计值对捷联惯导实时进行误差修正。

4 仿真与结论

首先设计载车的行驶轨迹，尽量模拟真实行驶环境，综合设计了匀速、加速、减速、转弯、爬坡、下坡、停止等多种运动形式。假设：初始位置为北纬34°20.163′，东经108°56.279′，海拔高度320 m；初始速度为0 m/s；初始航向角为30°，俯仰角为0°，横滚角为0°（均随机设定）；行驶时间为3600 s，最高速度为25 m/s，总行驶路程约为61.5 km。利用Matlab仿真生成载车行驶轨迹，如图2所示。

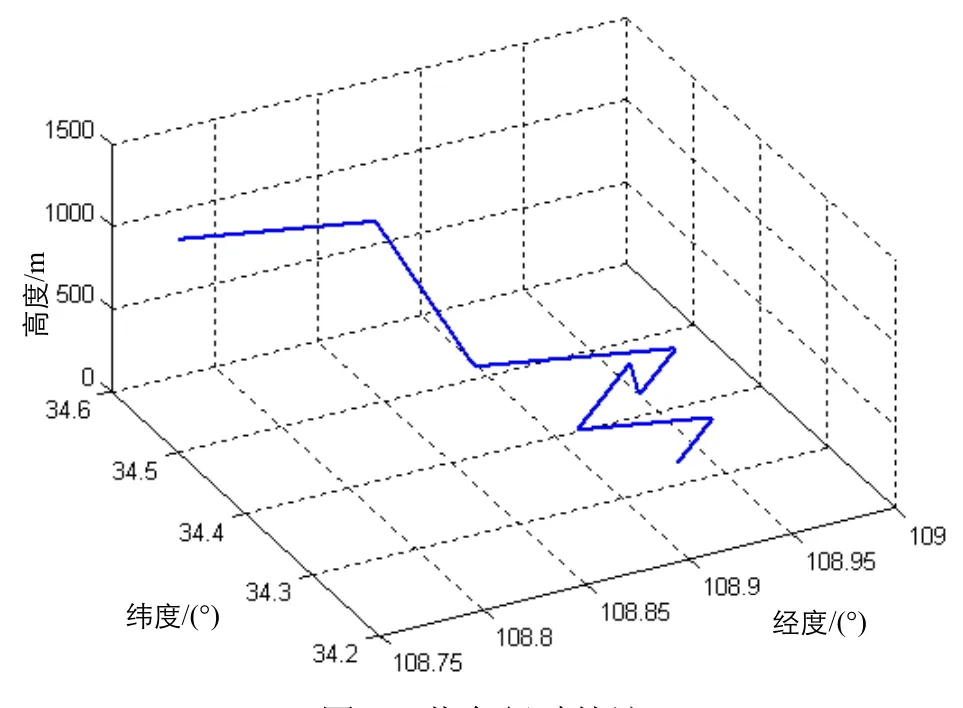
图2 载车行驶轨迹Fig.2 Driving trajectory of the vehicle

基于上述载车行驶轨迹，对文中所研究的里程计在线标定方法进行仿真验证。设：里程计标度因数误差为 0.5%；陀螺常值漂移为 0.01 (°)/h，随机游走为加速度计常值偏置为 10-4g，随机游走为惯导初始水平姿态误差为2′，方位误差为5′，初始速度误差为0 m/s，初始位置误差为10 m；航位推算初始误差同于惯导系统。仿真结果如图 3～6所示，其中图3为里程计标度因数误差的在线标定结果，图4～5则为针对里程计误差标定、未标定两种情况下分别进行组合定位定向的结果比较（“实线”为标定情况下的仿真结果，“虚线”为未标定情况下的仿真结果）。

图3 里程计标度因数误差的标定结果Fig.3 Calibration result of odometer’s scale factor error

根据图3可以看出，利用文中提出的方法能够有效地估计标定出里程计的标度因数误差，滤波收敛速度较快，估计效果理想，到了仿真第790 s估计结果就基本达到稳态，而且与仿真设定值（0.5%）非常接近。根据图4～5则可以看出，在相同的行驶轨迹与仿真条件下，里程计误差标定情况下的组合定位定向精度要明显高于未标定情况下：经过3600 s的仿真，前者的水平定位精度达到24.5m，高度精度达到11.8 m，航向精度最终达到1.6′，水平姿态精度则达到0.1′，而后者的定位误差则呈现出明显的发散趋势，其中水平位置误差最大为165.9 m，高度误差最大为14.1 m；至于后者的定向精度则是略低于前者，其中后者的航向精度最终达到3.1′，水平姿态精度达到0.2′，但是前者的航向误差收敛速度更快，收敛效果更好。由此可见，里程计的标度因数误差对捷联惯导/里程计组合定位定向的精度造成明显的影响，必须对其进行有效的在线标定以确保组合定位定向精度。

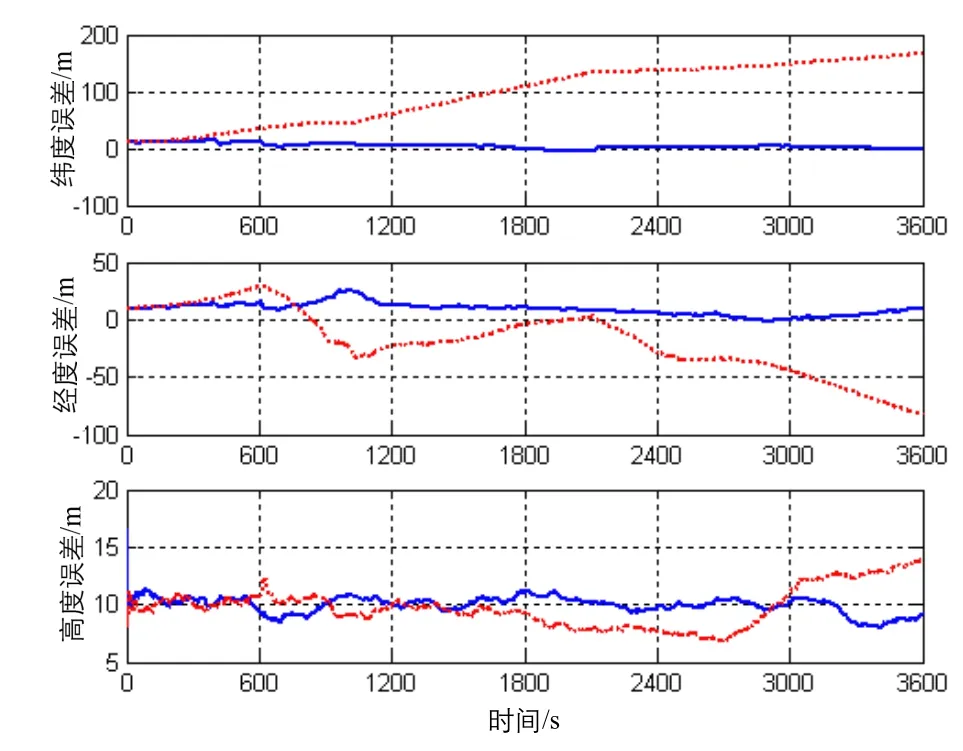
图4 组合定位定向的位置误差Fig.4 Position errors of integrated positioning and heading

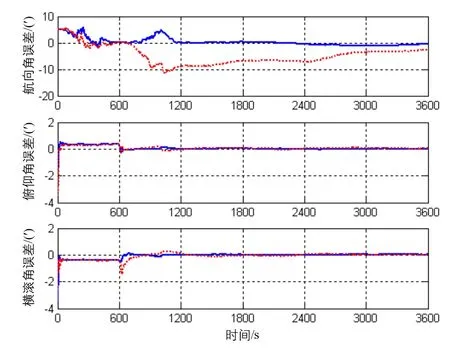
图5 组合定位定向的姿态误差Fig.5 Attitude errors of integrated positioning and heading

综上所述，为了降低里程计误差对捷联惯导/里程计组合定位定向精度的影响，本文利用车辆运动约束条件研究了里程计误差的在线标定方法，通过对里程计标度因数误差进行建模，并将航位推算的速度输出沿车体坐标系x、z轴上的投影引入量测，从而利用卡尔曼滤波实现了对里程计标度因数误差的在线估计标定。该方法标定效果显著，简单易行，而且对载车行驶线路、特定机动不作特殊要求，因此具有良好的工程应用前景。

（References）：

[1] Georgy J, Noureldin A, Korenberg M J, et al. Modeling the stochastic drift of a MEMS-based gyroscope in gyro/ odometer/GPS integrated navigation[J]. IEEE Transactions on Intelligent Transportation Systems 2011, 11(4): 856-872.

[2] Kim S B, Bazin J C, Lee H K, et al. Ground vehicle navigation in harsh urban conditions by integrating inertial navigation system, global positioning system, odometer and vision data[J]. IET Radar, Sonar and Navigation, 2011, 5(8): 814-823.

[3] Georgy J, Karamat T, Iabal U, et al. Enhanced MEMSIMU/odometer/GPS integration using mixture particle filter[J]. GPS Solutions, 2011, 15(3): 239-252.

[4] 赵洪松, 缪玲娟, 沈军. 捷联惯导/里程计高精度组合导航算法[J]. 兵工学报, 2014, 35(4): 433-440. Zhao Hong-song, Miao Ling-juan, Shen Jun. High accuracy algorithm for SINS /Odometer integrated navigation system[J]. Acta Armamentarii, 2014, 35(4): 433-440.

[5] Zhang X, Liu P, Yi X, et al. Observability analysis of SINS/odometer integrated navigation[C]//2014 IEEE Chinese Guidance, Navigation and Control Conference: 148-152.

[6] 朱立彬, 王玮. 轮胎充气温度对光电里程仪标度因数影响的标定算法[J]. 中国惯性技术学报, 2011, 19(2): 190-193. Zhu Li-bin, Wang Wei. Calibration of optical odometer’s scale factor with tire inflation temperature[J]. Journal of Chinese Inertial Technology, 2011, 19(2): 190-193.

[7] 罗强力, 韩军海. 基于递推最小二乘法的捷联惯导与里程计组合导航系统标定[J]. 导弹与航天运载技术, 2014(1): 29-33. Luo Qiang-li, Han Jun-hai. Calibration of strapdown inertial navigation system/odometer integrated navigation system based on recursive least square method[J]. Missiles and Space Vehicles, 2014(1): 29-33.

[8] Zhu L. Influence of tire temperature on odometer's scale factor[C]//2012 Fifth International Conference on Intelligent Computation Technology and Automation. IEEE, 2012: 690-693.

[9] Aoki H, Sam Ann R, Tanaka A, et al. Odometer correction method using disturbed environmental magnetic field[C]//Consumer Electronics. IEEE, 2014: 463-464.

[10] 杨波, 彭培林, 王跃钢, 等. 里程计辅助捷联惯导运动基座对准方法[J]. 中国惯性技术学报, 2013, 21(3): 298-301. Yang Bo, Peng Pei-lin, Wang Yue-gang, et al. Alignment method of strapdown inertial navigation system aided by odometer on moving base[J]. Journal of Chinese Inertial Technology, 2013, 21(3): 298-301.

[11] 付强文, 秦永元, 李四海, 等. 车辆运动学约束辅助的惯性导航算法[J]. 中国惯性技术学报, 2012, 20(6): 640-643. Fu Qiang-wen, Qin Yong-yuan, Li Si-hai, et al. Inertial navigation algorithm aided by motion constraints of vehicle[J]. Journal of Chinese Inertial Technology, 2012, 20(6): 640-643.

[12] 杨波, 王跃钢, 郭志斌, 等. 车载惯导系统动基座高精度自主式对准方法[J]. 中国惯性技术学报, 2015, 23(5): 580-584. Yang Bo, Wang Yue-gang, Guo Zhi-bin, et al. Accurate independent alignment method of inertial navigation system for vehicles on moving base[J]. Journal of Chinese Inertial Technology, 2015, 23(5): 580-584.

Online calibration method for odometer’s errors based on vehicle motion constraints

LI Yan1, YANG Bo2, XUE Liang2, ZHOU Xiao-gang2
(1. College of Information, Chang’an University, Xi’an 710064, China; 2. Department of Automation, The Second Artillery Engineering University, Xi’an 710025, China)

In order to reduce the odometer errors’ influences on the accuracy of integrated positioning and heading in strapdown inertial navigation system/odometer (SINS/OD), an online calibration method for odometer errors based on vehicle motion constraints was studied. The error of odometer’s scale factor was modeled, and the error model of dead reckoning (DR) was deduced. The projections of DR’s velocity outputs on the transverse and vertical of vehicle body were chosen as one part of the observations, and the velocity and position outputs of SINS and DR were chosen as the other part of the observation. Then the optimal estimations of the odometer’s scale factor error and other state variables were obtained by a Kalman filter. Thus the online-calibration of odometer errors was achieved. Simulation results show that, the odometer’s scale factor error can be effectively calibrated by this method, thus the positioning and heading accuracy of the integrated SINS/OD can be ensured.

odometer error calibration; vehicle motion constraints; integrated position and orientation determination; dead reckoning; Kalman filter

V249.3

：A

2016-04-08；

：2016-07-28

李艳（1972—），女，讲师，从事计算机应用、信息融合技术研究。E-mail: chaiyan1026@163.com

1005-6734(2016)04-0485-05

10.13695/j.cnki.12-1222/o3.2016.04.012