磁化悬浮-感应驱动型动量球系统

范 达，范春石，贺 杨，宋 坚，张 南

（中国空间技术研究院 钱学森空间技术实验室，北京 100094）

磁化悬浮-感应驱动型动量球系统

范 达，范春石，贺 杨，宋 坚，张 南

（中国空间技术研究院 钱学森空间技术实验室，北京 100094）

磁悬浮动量球是一种高功能密度比的微小卫星三轴姿控部件。磁悬浮与驱动原理的选择、磁极拓扑结构的布局以及传感方式的选用，从悬浮-旋转兼容性和空间结构干涉性上制约着磁悬浮动量球的可实现性。提出了一种新型的悬浮-旋转解耦、结构简单紧凑的磁化悬浮-感应驱动型动量球系统，以单轴实现为例详细论述了系统组成与工作原理，对子模块的设计、硬件实现与建模开展了研究。针对开环不稳定悬浮系统，提出一种基于构造法的控制参数设计方法，并给出了系统的三轴拓展方式。仿真和实验结果表明，该系统可以实现悬浮与旋转功能，悬浮球体在有旋转和无旋转时的位移稳定度分别约为1.6 μm和4.7 μm，球形转子的转速可达720 r/min。

磁悬浮；动量球；三轴姿控；磁化悬浮；感应驱动

微小卫星的发展对高功能密度比的空间姿控部件提出了新需求，磁悬浮动量球是一种新型的角动量交换部件，它采用磁悬浮轴承代替传统的机械轴承实现球体悬浮，并通过控制旋转磁场的矢量方向使悬浮球体可沿任意轴进行旋转，从而实现悬浮球体与星体在任意方向上的角动量交换。动量球以其“以一代三”的万向角动量交换的特点，使其有潜力替代传统的飞轮或动量轮成为未来空间姿控的主流部件。

文献[1-4]研制了一种永磁式球形转子的磁悬浮动量球，转子上嵌有分布式永磁体，然而此类动量球的磁场模型复杂，悬浮与旋转具有强耦合特性，旋转控制需要基于球形转子的姿态实时解算，难度极大，仅实现了极低转速下的三轴功能。文献[5-6]讨论了一种基于感应电机原理的动量球，实现了单轴悬浮与旋转，但其定子磁极为圆周分布，在三轴拓展时会产生空间干涉。文献[7]研究了一种基于磁滞电机原理的磁悬浮动量球，实现了单轴的悬浮和旋转，但由于此类动量球带有较强的磁滞特性，使其控制不具有重复性，且其定子磁极的拓扑结构同样不便拓展为三轴。文献[8]采用铁芯复用的方式，利用多套线圈将悬浮与旋转一体化，磁极结构具有三轴拓展性，但在高速应用下，其旋转驱动磁场会对电涡流位移传感器产生较严重的干扰。

本文提出了一种新型的磁化悬浮-感应驱动型动量球，具有悬浮-旋转解耦，结构简单紧凑，可三轴拓展等特点。以单轴实现为例详细论述了其系统组成与工作原理，对子模块的设计、硬件实现与建模开展了研究，并针对开环不稳定悬浮系统提出一种基于构造法的控制参数设计方法，通过仿真和实验得到验证，最后给出其三轴拓展方式及仍需进一步研究的问题。

1 磁化悬浮-感应驱动型动量球系统原理

图 1所示为磁化悬浮-感应驱动型动量球的系统组成示意图，系统可划分为五个功能模块：1）由悬浮线圈与空心铁球组成的被控对象（悬浮功能部分）；2）由激光器、硅光电池及光电位移检测电路组成的差分式光电位移检测模块；3）悬浮驱动电路；4）悬浮控制电路；5）由旋转控制电路、旋转驱动电路及旋转驱动线圈组成的旋转驱动模块。

前4个模块用于实现对空心铁球的悬浮控制。系统通过差分式光电位移检测模块获得空心铁球的位置。当检测到铁球偏离中心位置时，由悬浮控制电路根据偏离信息产生控制信号，经悬浮驱动电路进行电流放大后对悬浮线圈上加载的电流进行调节，从而动态调整施加到空心铁球上的电磁悬浮力，克服扰动，使空心球体重新回到中心位置。

第 5个模块用于实现对悬浮后的空心铁球的旋转驱动。通过旋转控制电路产生两相交流信号，经旋转驱动电路进行电流放大后加载到四个线圈上，从而产生旋转磁场，利用电磁感应效应带动空心铁球跟随磁场旋转。球形转子对定子磁极（固定于卫星本体上）产生的反作用电磁力矩可以用于实现卫星的空间姿态控制。

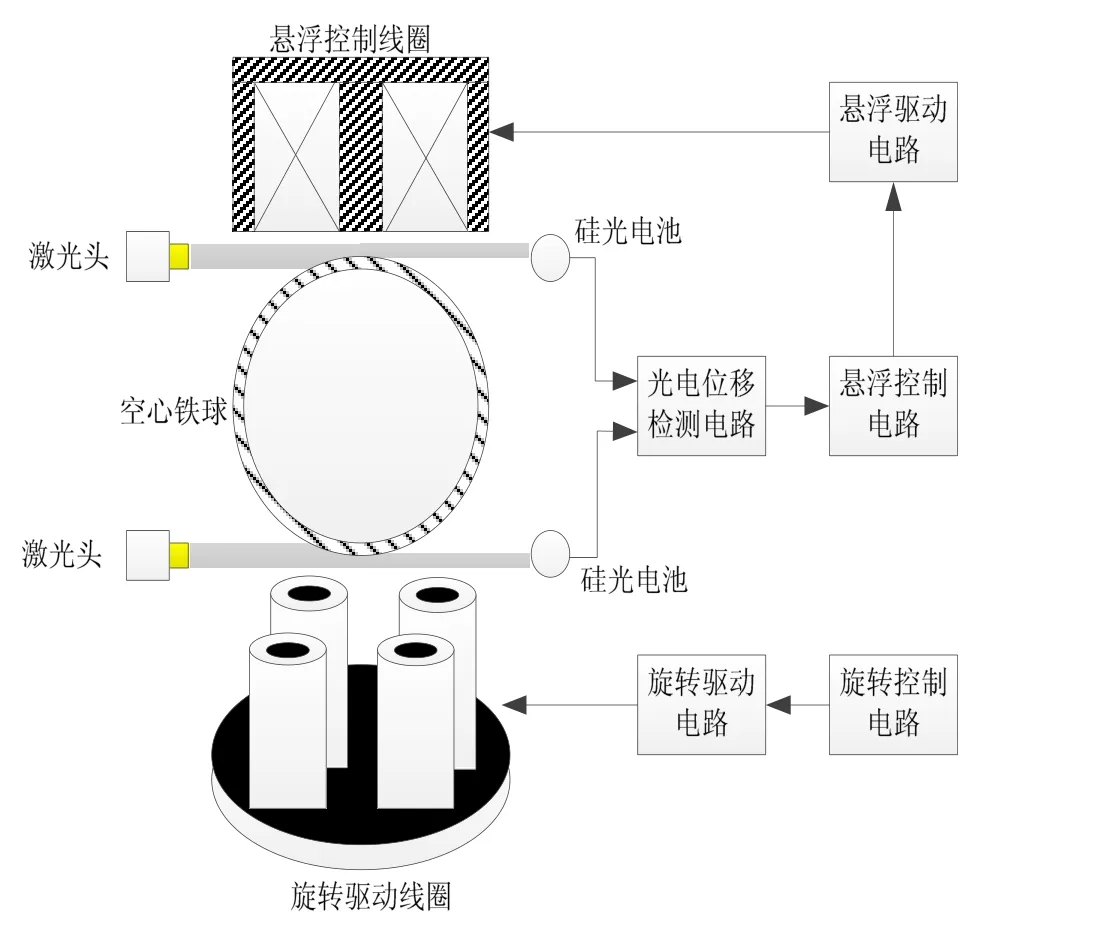
图1 磁化悬浮-感应驱动型动量球的系统组成Fig.1 System composition of momentum sphere of magnetization suspension and induction driving

2 子模块分析、设计与实现

2.1 磁悬浮力物理模型

当悬浮控制线圈的结构与空心铁球的尺寸确定后，磁悬浮力仅由悬浮控制线圈上加载的电流i以及空心铁球与悬浮控制线圈的间隙x决定。

悬浮控制线圈采用外轮廓为圆柱形的罐形铁芯，如图2(a)，它与空心铁球所构成的总电感L随间隙x的变化一般具有如图2(b)曲线所示的规律。

对于图2(b)中的曲线，可以用式(1)进行较好地近似数学描述[9-10]，从而方便后继的理论与仿真分析。

图2 悬浮线圈及其电感Fig.2 Levitation coil and its inductor

式中，L1为将空心球移走时（x=∞）悬浮控制线圈的电感，L0为空心铁球与悬浮控制线圈吸在一起时（x=0）的电感增量。根据电磁理论可知系统能量为

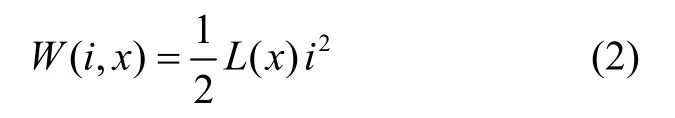
根据虚功原理将系统能量对间隙求偏导可得电磁悬浮力的表达式为

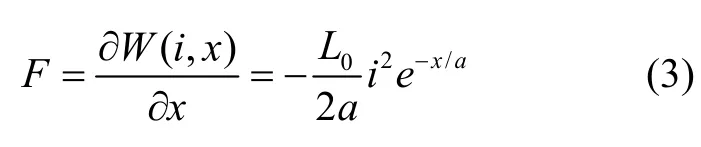
式中，负号代表是吸引力。设x0为稳定悬浮时空心铁球与控制线圈的标称间隙（实际设定为 1.5 mm），xd为接近于0的微小动态调节位移，即有：

设I0为稳定悬浮时的静态电流（实际为0.526 A），id为接近于0的微小动态调节电流，即有：

将(4)、(5)两式代入式(3)作泰勒展开并忽略高阶小项，得：

显然，式(6)中等号右边的第一项大小与空心铁球的重力相等：

式中，M为空心铁球质量，g为重力加速度。令

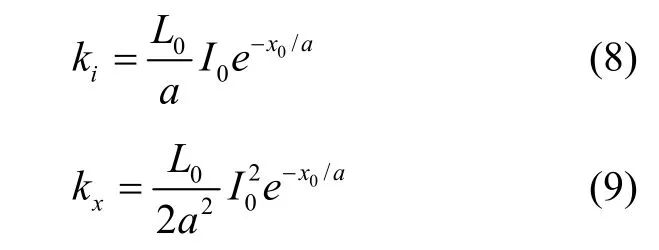
则式(6)可转化为

式中，ki为力-电流系数，kx为力-位移系数。由式(10)可以看出，磁悬浮力是一种与位移有正反馈关系的力，构成的系统具有负刚度特性，若不加闭环反馈控制，系统将失稳。

2.2 差分式光电位移检测

差分式光电位移检测由激光器、硅光电池及光电位移检测电路组成。激光器发出两束平行激光分别扫掠空心铁球的上下边缘。光束被空心铁球部分遮挡，并由对应的光电池接收未被遮挡的部分光束。根据接收光照面积之差可获取球体位置，如图3所示。

图3 差分式光电位移检测Fig.3 Detection of differential photoelectric displacement

相比于只用单边光电位移检测（如只用上面的光电池通道），差分式光电位移检测一方面可以抑制共模噪声，获得更优的信噪比，另一方面也能提高检测零点附近的线性度，减弱系统的非线性环节，增强悬浮控制的稳定裕度。更为重要的是，差分方式可以在三轴拓展应用中，使球形转子的三轴位移检测相互解耦。当图3中的球体沿水平方向有位移0.5 mm时，采用单边式和采用差分式光电位移检测的输出因耦合引起的变化量如图4所示，仿真参数为：球半径25 mm，光斑半径为1.5 mm，单边光电池无遮挡照射时的输出为5 V，上下两光斑的中心间距为球体的直径50 mm。

图4 光电位移检测受正交轴位移耦合的影响特性Fig.4 Characteristics of photoelectric displacement detection influenced by orthogonal-axis displacement coupling

由图4中的曲线对比可以看出，差分式光电位移检测受水平位移引起的最大输出耦合变化比单边光电位移检测小一个量级，尤其是当球体位于中心位置时，对水平方向的交轴向位移有理想的解耦性。

2.3 悬浮驱动电路

悬浮驱动电路采用功率三极管 BUZ350搭建，如图5所示，可将控制电压信号VG转化为加载到悬浮控制线圈上的驱动电流i。

根据实际稳定悬浮时电流的静态工作点I0即0.526 A，可查询出BUZ350在工作点的跨导值 gfs约为 2.2 Ω-1，Rs取为1 Ω，从而可计算得到驱动环节的动态电压/电流增益系数为

图5 悬浮驱动电路Fig.5 Suspension driver circuit

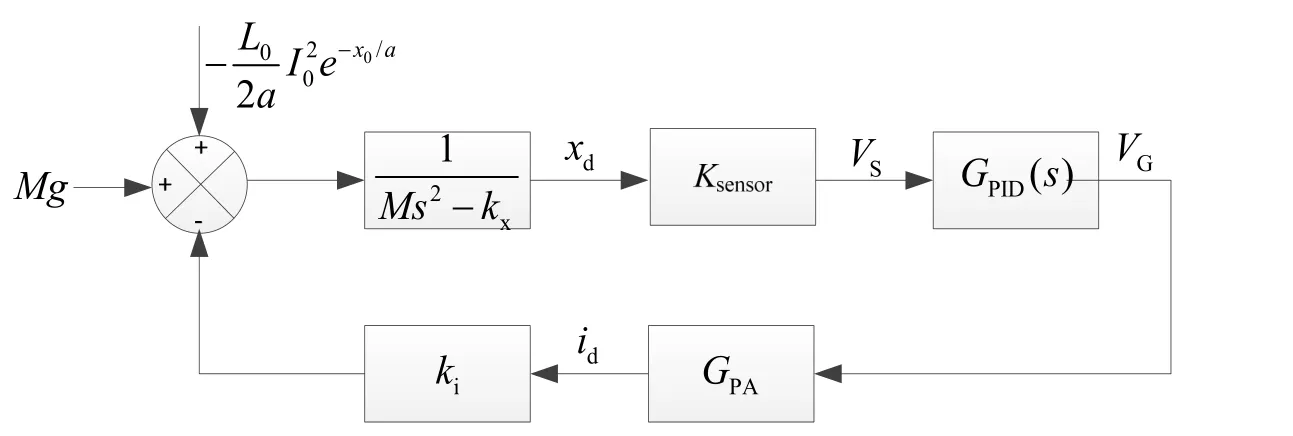
图6 悬浮系统框图Fig.6 Block diagram of the levitation system

2.4 悬浮控制

基于上述分析，根据线性化处理后的各个环节的传递函数建立悬浮控制系统框图如图6所示，从中可以看出此系统在开环时具有负刚度kx，开环是不稳定的，必须设计PID控制器GPID，构成闭环结构，将系统改造为正刚度系统，从而使系统稳定。引入PID控制器构成闭环反馈后，系统的传递函数为

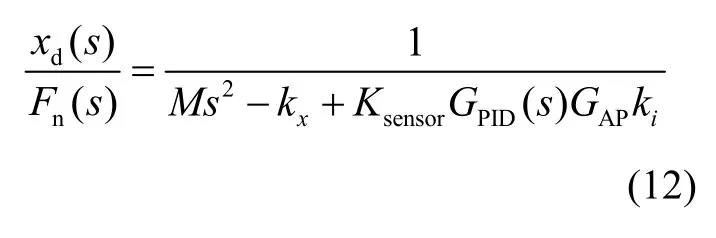
式中，Fn为重力与静态悬浮力之差（或可视为外界扰动力）。

传统的 PID参数设计通常采用经验试凑法，具有一定盲目性，对于磁悬浮这种开环不稳定系统试凑方式更显效率较低。在此我们采用构造法进行PID参数的设计。首先，在PID控制算法中只引入PD（比例微分）环节：

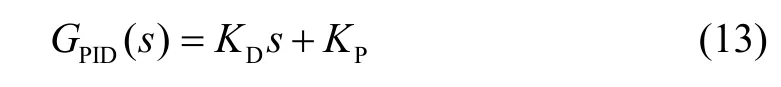
将系统构造为一个典型的正刚度二阶系统：

式中，ξ为阻尼比，ωn为自然角频率。考虑到在地面悬浮时受到重力的作用且悬浮间隙较小，要使空心铁球可以稳定悬浮，需要较快的反馈调节速度，同时不能有太大的速度过冲，因此，取较大的阻尼比ξ为1.25，自然角频率ωn为440 rad/s（70 Hz）。将式(13)代入式(12)并与式(14)对比，可得：

当其它参数通过实验测试获得后（参数获取见第 4节部分实验），便可通过式(15)(16)直接计算出比例与微分控制的参数，此时再引入合适的积分控制。实际系统中，各环节参数如表 1所示，当控制参数KI设为1时，闭环系统的三个特征根为负根，根据劳斯判据可知系统稳定。

表1 悬浮系统参数Tab.1 Parameters of the levitation system

2.5 旋转驱动模块

旋转驱动线圈采用两相四极的模式，如图7所示，对角的两个线圈首首串连成一相。它与球形转子实际上可等效为一系列间隙不等的盘式电机，当在旋转驱动线圈上加载两相电流时，产生的旋转磁场将驱动悬浮的球形转子进行旋转。由于空心铁球悬浮后没有机械摩擦，只需要很小的旋转力矩便可以实现驱动球体转动。

图7 旋转驱动线圈Fig.7 Coil for rotatory driving

3 系统仿真

采用Matlab/Simulink对悬浮系统进行仿真，仿真系统如图8所示。在仿真过程中，磁悬浮力物理模型采用的是非线性模型，而PID控制参数采用的是根据系统平衡点处局部线性化后所设计的参数，即第2部分中表1中的参数。

分别采用PD和PID控制对系统进行仿真，仿真结果如图9和图10所示。由仿真结果可以看出，两种方式控制均可使系统稳定，且总驱动电流约为0.53 A与期望值吻合较好。带积分控制的系统由于积分饱合效应而过冲较大，因此其达到稳定态的时间较长，但相比于无积分的PD控制，带积分的系统最终稳定时将没有位移静差。

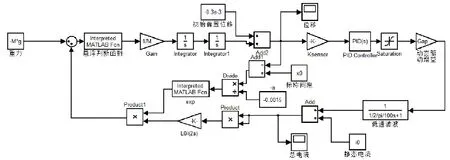
图8 Matlab/Simulink仿真系统图Fig.8 Simulation system diagram based on Matlab/Simulink

图9 PD控制下的仿真曲线Fig.9 Simulation curves under the PD control

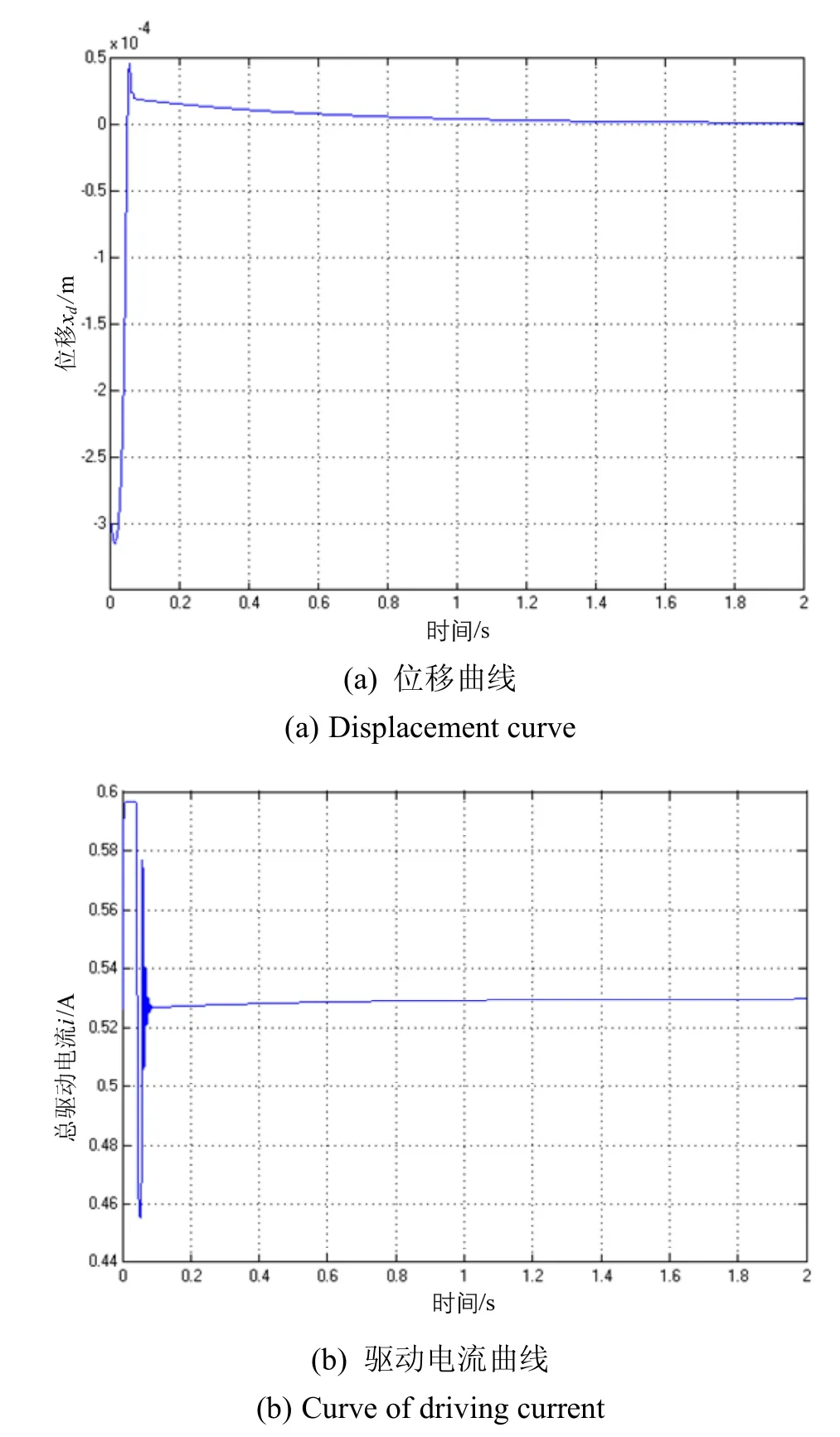
图10 PID控制下的仿真曲线Fig.10 Simulation curve under the PID control

4 实 验

实际实验系统原型如图11所示。采用第2节所设计的PID控制参数并引入积分分离方法进行实际悬浮控制，测得的悬浮过程位移曲线如图12(a)所示，从示波器波形可以看出，空心铁球可以实现稳定悬浮，平稳时的波形跳动范围约为20 mV，可估算出悬浮控制稳定度约1.6 μm。实验结果表明：采用构造法进行控制参数设计可以实现良好的实际控制效果，且这种方法设计过程简单高效，可程序化计算出控制参数而不需要试凑。

当旋转驱动电流频率为50 Hz，幅值为0.2 A，旋转驱动线圈顶部与空心铁球底部在同一平面时，由激光转速测量仪测得空心铁球的稳定转速约为 720 r/min。加载旋转驱动后悬浮依然稳定，如图 12(b)所示，从示波器的波形可以看出，此时的检测电压波动为60 mV左右，约为4.7 μm，主要影响因素来自于：1）旋转电磁力矩的扰动；2）球形转子质量分布不均，旋转后由于动不平衡造成球体晃动。

图11 磁化悬浮-感应驱动型动量球实验系统Fig.11 Experiment system of momentum sphere of magnetization suspension and induction driving

图12 悬浮控制与旋转驱动实验Fig.12 Experiments of levitation control and rotation driving

5 三轴系统拓展

以上分析与实验是针对单轴的研究，但是通过在前后左右增加两组相同的组件，上述的单轴系统可以拓展为如图13(a)所示的三轴系统，每一轴都可以实现位移控制与旋转驱动，从而通过三个轴的力矩合成便可实现让球绕任意轴进行旋转的目的。更进一步，若采用线圈复用技术，使旋转驱动绕组同时具备位移控制的功能，可以将系统拓展成为如图13(b)所示的对称三轴系统，这样同一个轴可以进行双边旋转驱动，可为星上应用提供冗余备份。

图13 三轴动量球系统Fig.13 Three-axis momentum sphere system

6 结 语

磁化悬浮-感应驱动型动量球所采用的原理可使悬浮和旋转解耦，降低了控制与驱动的复杂度；而差分式光电位移检测实现了三轴位移检测解耦，同时配合四齿驱动组件的拓扑结构，使系统构成了紧凑的空间布局。磁化悬浮-感应驱动型动量球是一种便于实现三轴拓展的磁悬浮动量球系统。

然而，以上工作只是开展了此新型系统的可行性初步研究，后续还需要通过进一步深入研究改进系统，主要有以下几方面：

1）三轴系统轴间磁耦合分析与补偿控制；

2）球形转子的编码与测速方法，使球形转子沿任意轴旋转的转速可测量或解算，实现转速闭环；

3）优化磁极结构、球转子材料及焊接工艺，提高磁驱动效率；

4）通过磁场调制解决球形转子动不平衡引起的跳动；5）任意轴电磁力矩的生成控制方法与标定；

6）选择合适的软材料设计止挡，限制球转子在线性范围内平动同时起到支撑保护作用。

（References）：

[1] Rossini L, Chételat O, Onillon E, et al. Force and torque analytical models of a reaction sphere actuator based on spherical harmonic rotation and decomposition[J]. IEEE/ASME Transactions on Mechatronics, 2013, 18(3): 1006-1018.

[2] Rossini L. Electromagnetic modeling and control aspects of a reaction sphere for satellite attitude control[D]. Lausanne: Swiss federal Institute of Technology in Lausanne, 2014.

[3] Kahlen K, Voss I, Priebe C, et al. Torque control of a spherical machine with variable pole pitch[J]. IEEE Transactions on Power Electronics, 2004, 19(6): 1628-1634.

[4] Rossini L, Onillon E, Chételat O, et al. Closed-loop magnetic bearing and angular velocity control of a reaction sphere actuator[J]. Mechatronics, 2015, 30: 214-224.

[5] Kim D K, Yoon H, Kang W Y, et al. Development of a spherical reaction wheel actuator using electromagnetic induction[J]. Aerospace Science & Technology, 2014, 39: 86-94.

[6] Iwakura A, Tsuda S, Tsuda Y. Feasibility study on three dimensional reaction wheel[C]//Proceedings of the School of Engineering. Tokai University, Series E, vol.33, 2008: 51-57.

[7] Lei Zhou. Magnetically suspended reaction sphere with one-axis hysteresis drive[D]. Massachusetts: Massachusetts Institute of Technology, 2014.

[8] 刘蕾. 驱动磁悬浮球旋转的技术研究[D]. 南京: 南京航空航天大学, 2013. Liu Lei. Research on the driving technology for magnetic levitation ball rotation[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013.

[9] Wong T H. Design of a magnetic levitation control system -An undergraduate project[J]. IEEE Trans. on Education, 1986, E-29(4): 196-200.

[10] Naumovic M B. Modeling of a didactic magnetic levitation system for control education[C]//IEEE 6th International Conference on Telecommunications in Modern Satellite, Cable and Broadcasting Service. 2003: 783-786.

Momentum sphere system of magnetization suspension and induction driving

FAN Da, FAN Chun-shi, HE Yang, SONG Jian, ZHANG Nan
(China Academy of Space Technology, Qian Xuesen Laboratory of Space Technology, Beijing 100094, China)

The magnetic levitation momentum sphere used in a micro-satellite is a three-axis attitude control component with high function-to-density ratio. The realizability of the magnetic suspension momentum sphere, in terms of the interference capability of the spatial structure and the compatibility between suspension and rotation, is restricted by the selection of magnetic levitation and driving principle, the choice of the layout of the magnetic pole topology and the selection of sensing way. A new kind of magnetic suspension momentum sphere system with simple and compact structure is realized by magnetization suspension and induction driving, which is decoupled between suspension and rotation. The system composition and working principle are discussed by using one-axle as an example. The submodule design, hardware implementation and modeling are studied. Through structured approach, a design method of the control parameters is proposed for the unstable levitation system in open-loop state, and a three-axis development way for this system is introduced. Simulation and experimental results show that suspension and rotation can be realized by this system. The displacement stabilities of the suspended sphere with and without rotation are about 1.6 μm and 6 μm, respectively, and the speed of the spherical rotor can reach 720 r/min.

magnetic suspension momentum; three-axis attitude control; magnetization levitation; induction driving

V448.2

：A

2016-04-26；

：2016-06-16

“探索一代”研究基金（7131547）

范达（1985—），男，工程师，从事加速度计惯性仪表与悬浮控制研究。E-mail: fanda4312@sina.com

1005-6734(2016)04-0524-07

10.13695/j.cnki.12-1222/o3.2016.04.018