基于自相关特性的经验模态分解微机械陀螺去噪方法
2016-04-19刘晓光郝沙沙王光磊娄存广刘秀玲
刘晓光,郝沙沙,王光磊,娄存广,刘秀玲
(1. 河北大学 电子信息工程学院,保定 071002;2. 河北省数字医疗工程重点实验室,保定 071002)
基于自相关特性的经验模态分解微机械陀螺去噪方法
刘晓光1,2,郝沙沙1,2,王光磊1,2,娄存广1,2,刘秀玲1,2
(1. 河北大学 电子信息工程学院,保定 071002;2. 河北省数字医疗工程重点实验室,保定 071002)
陀螺的噪声是影响组合导航系统精度的重要因素之一。以农机多传感器组合导航系统为研究背景,在分析经验模态分解去噪和小波去噪的基础上,提出了一种基于自相关特性的经验模态分解去噪方法。该方法根据本证模态函数分量的自相关函数特性,提出了一种含噪本证模态函数筛选策略。该方法能够自适应地确定主要含噪的本证模态函数分量,避免了需要人为确定的不足;同时,结合改进小波阈值去噪的优势,避免了将混叠在噪声中的有效信号完全消除,使其具有一定的自适应性。为了验证方法的有效性,利用农机组合导航系统中微机械陀螺的实际输出数据,分别采用改进阈值小波去噪方法、经验模态分解去噪和改进的经验模态分解去噪方法进行了对比试验。结果表明,改进经验模态分解去噪方法的效果要优于前者,在一定程度上能够改善农机多传感器组合导航系统的定位精度。
经验模态分解;微机械陀螺;去噪;数据处理
微机械陀螺是一种应用非常广泛的一种测量角加速度的传感器。微机械振动陀螺具有体积小、功耗低、成本低、耐温范围广和可批量生产等优点。在惯性导航技术中,陀螺是现代精确导航、制导与控制系统的核心装备之一[1-2]。但微机械陀螺由于结构设计的局限性、温度漂移以及外围调理电路引起的噪声等原因必然使其输出信号含有误差。由于各种误差之间存在着复杂的耦合关系,所以微机械陀螺的误差呈现明显的非线性特征。因此,在应用微机械陀螺的数据之前,对其进行滤波降噪处理具有重要的意义。
经验模态分解(empirical mode decomposition,EMD)[3-4]将原始信号分解为多个本证模态函数(intrinsic mode function,IMF),其中低阶的IMF对应信号的高频部分,一般认为信号的噪声占主要成分,高阶的IMF对应信号的低频部分,认为有用信号占主要成分。整体上,EMD滤波体现了多尺度自适应滤波的特性,适用于处理非线性、非平稳的信号,所以EMD算法在工程领域得到了广泛的应用。
研究人员针对基于EMD的信号去噪进行了大量的研究[5-8]。席旭刚[9]等基于噪声统计特性利用 EMD方法来处理人体表面肌电信号,实验结果表明该方法能够保留更多的有效信息,提高信号的信噪比。崔冰波等[10]基于样本熵的模态筛选标准,提出了一种自适应的区间阈值滤波方法,并对光纤陀螺的数据进行了实验研究,结果显示该方法能够显著减小系统的航向角误差。Yang G L等[11]根据EMD分解的方差传播特性,提出了一种适用于高斯噪声的阈值选择方法,但该方法没有确定IMF筛选的确定方法。上述研究表明,EMD分解的方法与傅里叶变换完全不同,是一种更适合于时频局部化分析的方法。但EMD分解也有很多不足之处。单独采用EMD去噪会将相应的有用信息一并删除,从而影响重构信号的精度。
鉴于EMD分解的特点和小波阈值去噪的优势,本文将EMD和小波阈值去噪相结合,利用IMF分量的自相关函数的特性来确定含有噪声的IMF分量,然后利用小波阈值去噪的方法分别对含有噪声的IMF分量进行小波阈值去噪。该方法能够有效提高EMD对高频成分的分辨率,而且具有一定的自适应性。最后,利用陀螺的实际输出信号对该方法的有效性进行了验证,实验结果表明该方法优于常规的去噪方法。
1 改进的EMD去噪方法
1.1 常规EMD去噪方法的不足
原始信号经过EMD分解后得到多个由高频到低频分布的IMF,常规的EMD去噪方法认为噪声主要存在于高频段。EMD去噪的关键是如何确定含有噪声的高频IMF的阶次,但到底噪声分布在几阶IMF分量内没有一个明确的判别方法。此外,对于信噪比较低的信号,有用信号往往和噪声信号混叠在一起,采用直接删除部分高频IMF分量的方法虽然能够有效地去除噪声,但同时也损失了一定的有用信息,这必然会导致重构信号与真实信号之间存在一定的偏差。
1.2 基于自相关函数的含噪IMF阶次选择
针对常规EMD去噪不能确定含噪IMF阶次的问题,提出了利用自相关函数的特征来确定IMF阶次的方法。自相关函数反映了信号在不同时刻的相关程度,假设x(t)为随机信号,则其自相关函数为

根据随机噪声的统计特性,在零点处随机噪声的自相关函数最大,在其他时刻快速衰减到零值附近。而对于有效信号相对而言含有的噪声较少,其自相关函数同样在零点处有最大值,但由于其存在着一定的相互关联关系,在其他时刻也会呈现一定规律的变化,并不是快速地衰减到零值。基于信号自相关函数的特性,通过计算各IMF 分量的自相关函数来判断噪声占主体的IMF分量。
1.3 自适应阈值滤波
确定了含有噪声的IMF分量后,重点就是如何处理含噪的IMF分量。常规的方法是直接删除噪声占主体的IMF分量,但该方法会将有用的信息一起删除。鉴于小波阈值去噪的特点,对含有噪声的各IMF分量分别采用小波阈值去噪的方法进行处理。
小波阈值去噪方法采用文献[15]提出的改进小波阈值去噪方法,其阈值函数如式(2)所示:
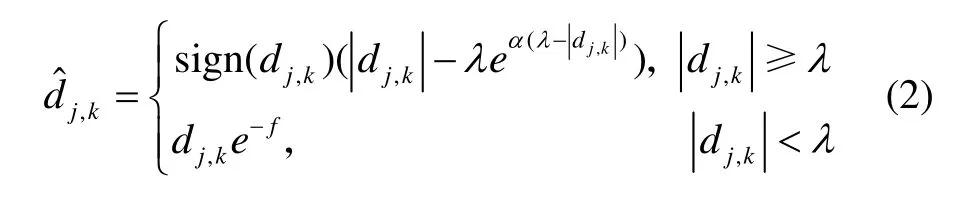
式中,λ为小波阈值,α为大于零的调节因子,f为信号的频率。
1.4 改进的EMD去噪流程
改进的EMD去噪的流程如图1所示。
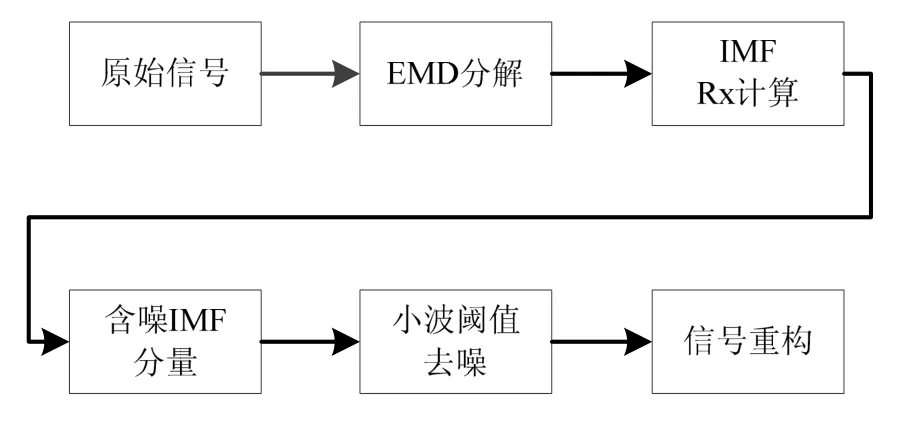
图1 改进的EMD去噪的流程Fig.1 Flow chart for improved EMD
具体过程为:
1)对原始信号进行 EMD分解,得到多个 IMF分量;
2)分别计算各IMF的自相关函数,然后根据自相关函数的特征,确定含噪的IMF分量;
3)对含噪的IMF分量,分别采用改进的小波阈值去噪方法进行处理;
4)最后利用处理后的IMF和未处理IMF重构出去噪后的信号。
2 实验分析
2.1 数据采集
本文的研究背景是农机多传感器组合导航系统研究。采用插秧机组合导航系统X轴陀螺的实际输出数据作为实验对象。首先将陀螺上电预热10 min,然后采集陀螺输出的原始数据,数据的采样频率为100 Hz,数据长度为430 000,持续时间约为1 h。图2所示为采集的陀螺静态数据。
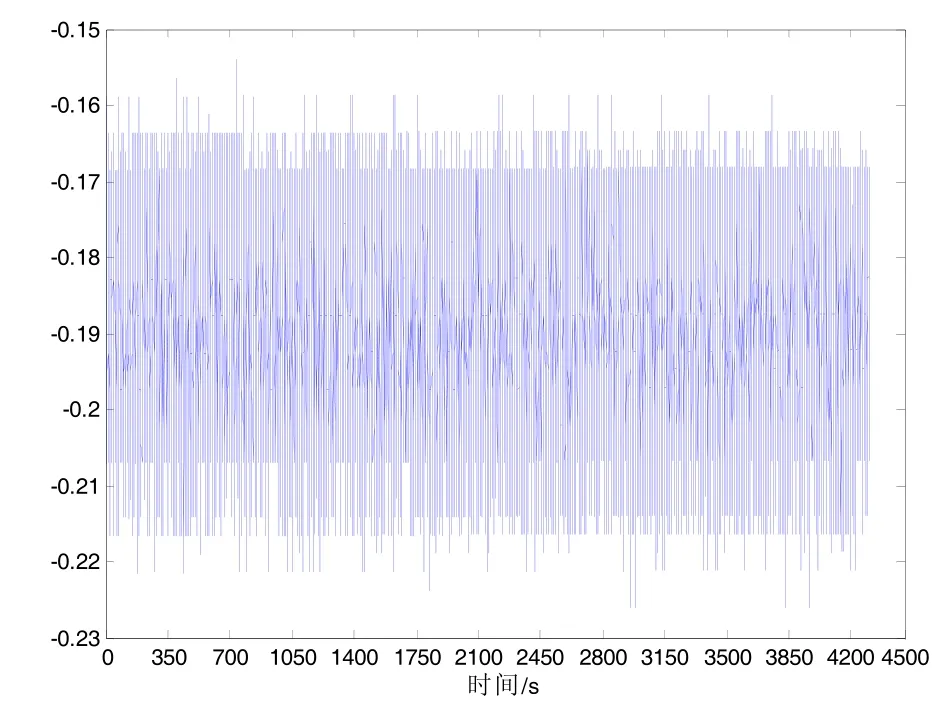
图2 X轴陀螺原始数据Fig.2 Original signal of X-axis gyro
2.2 试验结果与分析
对上述采集的数据进行EMD自相关分解,获得15阶IMF,如图3所示。分别计算各阶IMF的自相关函数,如图4所示。由于噪声的相关函数在零点处有最大值,在其它时刻快速衰减到零值附近,而陀螺的信号前后之间存在着一定的相关性,所以其自相关函数在零点处取最大值,在非零点处并不衰减为零值。根据这一特点由各阶 IMF的自相关函数,判定大约9到10阶IMF分量为噪声存在的主要分量。
为了能够准确地确定含噪的 IMF阶数,分别计算了各阶IMF分量的方差,如图5所示。
由图5可以看出,前9阶IMF自相关函数的方差都小于0.005,而10阶及其以上IMF自相关函数的方差明显呈现指数上升的趋势。因此,认定噪声主要存在于前9阶IMF,需要对其进行降噪处理。
对上述需要去噪处理的前9阶IMF采用改进的小波阈值法进行滤波处理,阈值,其中,σ为噪声标准方差,N为采样信号的长度。为了对比分析该方法的去噪效果,分别利用改进的小波阈值去噪方法、常规EMD去噪和改进的EMD去噪方法进行了对比实验,实验结果如图6所示。
由图6可以看出,原始信号经过去噪处理后,噪声信号明显得到了去除。
为了定量分析各方法的性能,对去噪后的信号分别分析了信噪比和方差两个特征,如表1所示。

图3 X轴陀螺数据的各阶IMF分量Fig.3 All IMF components of X-axis gyro signal

图4 各阶IMF分量的自相关函数Fig.4 Autocorrelation functions of All IMFs
由表1中数据可知,EMD方法的去噪效果稍低于小波去噪,而改进的EMD方法结合了EMD和小波去噪的优势,不论是在信噪比上还是时域特征上都优于前两种方法。

图5 各阶IMF自相关函数的方差Fig.5 Variances of autocorrelation functions for IMFs
3 结 论
EMD分解和小波分解的方法在很多领域都有广泛的应用。本文在常规EMD方法的基础上,针对常规EMD去噪不能准确判断主要含噪IMF的问题,依据噪声的自相关函数的特点,提出了一种判别主要含噪IMF的方法。针对含噪的IMF,结合小波阈值去噪的思想对其进行滤波处理,然后再重构出滤波后的信号。对比试验结果表明,利用该方法处理后,能够有效降低噪声的方差,提高信号的信噪比。将该方法应用于农机多传感器组合导航系统上,在一定程度上提高了系统的定位精度。

表 1 三种算法去噪效果对比Tab.1 Denoising effects of three algorithms

图6 原始数据与降噪数据对比Fig.6 Contrast between denoised data and original data
(References):
[1] 王巍. 惯性技术研究现状及发展趋势[J]. 自动化学报, 2013, 39(6): 723-729. Wang Wei. Status and development trend of inertial technology[J]. Acta aucomatica sinica, 2013, 39(6): 723-729.
[2] Wang W, Wang X F, Xia J L. The influence of Er-doped fiber source under irradiation on fiber optic gyro[J]. Optical Fiber Technology, 2012, 18(1): 39-43.
[3] Cheng J, YU D, Yang Y, et al. Research on the intrinsic mode function (IMF) criterion in EMD method[J]. Mechanical Systems and Signal Processing, 2006, 20(4): 817-824.
[4] 王婷. EMD 算法研究及其在信号去噪中的应用[D].哈尔滨: 哈尔滨工程大学, 2010. Wang Ting. Research on EMD algorithm and its Application in signal denoising[D]. Harbin: Harbin Engineering University, 2010.
[5] Shang Yue Z, Yuan Yuan L, Gong Liu Y. EMD interval thresholding denoising based on correlation coefficient to select relevant modes[C]//Control Conference. IEEE, 2015: 4801-4806.
[6] Damasevicius R, Vasiljevas M, Martisius I, et al. BoostEMD: An extension of EMD method and its application for denoising of EMG signals[J]. Elektronika Ir Elektrotechnika, 2015, 21(6): 57-61.
[7] 张强, 行鸿彦. 基于EMD方差特性的混沌信号自适应去噪算法[J]. 电子学报, 2015, 43(5): 901-906. Zhang Qiang, Xing Hong-yan. Adaptive denoising algorithm based on the variance characteristics of EMD[J]. acta Electronica Sinica, 2015, 43(5): 901-906.
[8] Piñeiro-Ave J, Blanco-Velasco M, Cruz-Roldán F, et al. Target detection for low cost uncooled MWIR cameras based on empirical mode decomposition[J]. Infrared Physics & Technology, 2014, 63(3): 222-231.
[9] 席旭刚,武昊,罗志增. 基于EMD自相关的表面肌电信号消噪方法[J]. 仪器仪表学报, 2014(11): 2494-2500. Xi Xu-gang, Wu Hao, Luo Zhi-zeng. De-noising method of the sEMG based on EMD autocorrelation[J]. Chinese Journal of Scientific Instrument, 2014(11): 2494-2500.
[10] 崔冰波, 陈熙源, 龚政仰. 基于经验模态概率分布的光纤陀螺信号处理[J]. 中国惯性技术学报, 2015, 23(5): 690-695. Cui Bing-bo, Chen Xi-yuan, Gong Zheng-yang. Fiber optic gyro signal processing based on empirical mode probability distribution[J]. Journal of Chinese Inertial Technology, 2015, 23(5): 690-695.
[11] Yang G, Liu Y, Wang Y, et al. EMD interval thresholding denoising based on similarity measure to select relevant modes[J]. Signal Processing, 2015, 109: 95-109.
[12] Wang Y H, Yeh C H, Young H W V, et al. On the computational complexity of the empirical mode decomposition algorithm[J]. Physica A Statistical Mechanics & Its Applications, 2014, 400(2): 159-167.
[13] Zhang Q, Wang L, Gao P, et al. An innovative wavelet threshold denoising method for environmental drift of fiber optic gyro[J]. Mathematical Problems in Engineering, 2016, 2016(3): 1-8.
[14] Mert A, Akan A. Detrended fluctuation thresholding for empirical mode decomposition based denoising[J]. Digital Signal Processing, 2014, 32(2): 48-56.
[15] 刘晓光, 胡静涛, 高雷, 等. 基于改进小波阈值的微机械陀螺去噪方法[J]. 中国惯性技术学报, 2014, 22(2): 233-236. Liu Xiao-guang, Hu Jing-tao, Gao Lei, et al. Micro mechanical gyro denoising method based on improved wavelet threshold[J]. Journal of Chinese Inertial Technology, 2014, 22(2): 233-236.
Micro mechanical gyro denoising method based on EMD autocorrelation
LIU Xiao-guang1,2, HAO Sha-sha1,2, WANG Guang-lei1,2, LOU Cun-guang1,2, LIU Xiu-ling1,2
(1. College of Electronic and Information Engineering, Hebei University, Baoding 071002, China; 2. Key Laboratory of Digital Medical Engineering of Hebei Province, Baoding 071002, China)
The gyro noises could significantly influence the precision of an integrated navigation system. Based on the analysis of conventional EMD and wavelet denoising, a denoising method based on empirical mode decomposition (EMD) autocorrelation is proposed by using multi-sensor integrated navigation system for agricultural machinery. The method proposes an intrinsic mode function (IMF) screening strategy based on autocorrelation function characteristics of the IMF, and can adaptively determine the main noise components of IMF to avoid the human intervention. Further more, the method combines the advantage of wavelet threshold denoising, avoiding the complete elimination of useful signals in the noises. In order to verify the validity of the method, a contrast test is made by using the improved wavelet threshold denoising, EMD denoising and the improved EMD denoising method, respectively, based on the actual output data of micro mechanical gyro in the multi-sensor integrated navigation system for agricultural machinery. Test results show that the improved EMD method is superior to the former, and it can, to some extent, improve the positioning accuracy of the multi-sensor integrated navigation system in agricultural machinery.
empirical mode decomposition; micro mechanical gyro; de-noising; data processing
U666.1
:A
2016-05-11;
:2016-07-28
河北省教育厅项目(QN2015071);保定市科技局项目(15ZG010)
刘晓光(1983—),男,讲师,从事农业装备组合导航研究。E-mail: lxg_hbu@163.com
1005-6734(2016)04-0537-05
10.13695/j.cnki.12-1222/o3.2016.04.020
