基于指数收敛的四旋翼无人机鲁棒自适应飞行控制

张居乾，任朝晖，周来宏，闻邦椿

（东北大学 机械工程与自动化学院，沈阳 110819）

基于指数收敛的四旋翼无人机鲁棒自适应飞行控制

张居乾，任朝晖，周来宏，闻邦椿

（东北大学 机械工程与自动化学院，沈阳 110819）

针对四旋翼无人机鲁棒自适应飞行问题，提出了一种基于指数收敛的控制方法。考虑到四旋翼系统的欠驱动、强耦合等非线性特性，采用线性化反馈控制策略实现对其轨迹追踪飞行能力的基本控制；针对线性化反馈控制易受系统内外部未知干扰等影响，采用基于指数收敛干扰观测器组合控制设计，实现四旋翼飞行的鲁棒与自适应控制；线性反馈及状态观测器控制系统基于指数收敛稳定。进行了仿真分析，结果表明，干扰观测器对四旋翼系统中存在的未知干扰具有很好的估计能力，所设计的基于指数收敛控制系统，结构简单，且具有较强的干扰抑制能力和较高的系统稳定性，满足四旋翼无人机的鲁棒及自适应飞行能力要求。

四旋翼无人机；轨迹追踪；反馈控制；干扰观测器；指数收敛；鲁棒自适应

四旋翼无人机近些年来被广泛应用于军事和民用领域，如侦查、营救、监控、航拍和测绘等。四旋翼机体主要由四个旋翼和机架构成，其设计简单，易于加工，价格低廉，携带方便，为使用者提供了极大的便利。相对于固定翼飞行器而言，四旋翼具有灵活的机动性、良好的操作性以及对各种复杂工作环境的高度适应性，其应用价值得到了广泛肯定与认可。

四旋翼无人机是一个具有多变量、欠驱动、强耦合以及干扰敏感等特性的复杂非线性系统[1]，对控制器设计要求较高，给其设计带来了难度。对四旋翼无人机的研究也主要集中在控制系统设计上。

针对四旋翼无人机系统高度非线性的特点，很多线性和非线性的控制方法被用于控制器的设计，例如PID、线性反馈、反步、滑模、自适应控制等[2-6]。在忽略非线性因素条件下，PID控制能够基本满足四旋翼的控制飞行[2]。考虑到其欠驱动、强耦合特点，线性反馈控制常用于其控制器的设计，但并未涉及未知干扰的影响；滑模控制可以有效解决抗干扰等非线性问题，易产生抖颤现象[7]。另外，一些非线性控制策略的组合开始被运用于四旋翼控制的设计上[8-14]。但是上述控制方法由于存在着种种难以解决的问题，如需要精确的数学模型，或需要大量的传感器，或控制结构过于复杂，难以实现。

本文针对四旋翼系统欠驱动、强耦合及其易受干扰影响等复杂非线性特点，设计了基于指数收敛的鲁棒自适应控制器。采用线性化反馈控制策略，解决了四旋翼系统多变量、欠驱动、强耦合的难题，在此基础上，设计了基于指数收敛干扰观测器，对干扰值进行实时估计并将其做输入作补偿，具有抗未知干扰的能力。该控制器的设计，实现了对四旋翼无人机的高精度的鲁棒自适应飞行控制。

1 四旋翼无人机动力学模型的建立

四旋翼无人机结构如图1所示。它由机架和四个呈“X”形对称分布的四个螺旋桨组成。通过实时控制和规律性改变四个螺旋桨转速，产生变化的升力和转动力矩，进而实现系统不同形式（前、后、左、右、升降、偏航）的运动，如表1所示。

为了实现对四旋翼无人机的控制，首先需要建立其动力学模型，并对其做了如下假设：

· 四旋翼机身为刚性结构体，并呈对称分布；

· 螺旋桨为刚性体，转动无形变且位置固定。

图1 四旋翼无人机结构图Fig.1 Structure of quadrotor

本文基于牛顿-欧拉方程建立了四旋翼无人机系统的动力学模型。首先分别定义地坐标系与机体坐标系分别为 E(x,y,z)和B(xb,yb,zb)。定义机体坐标系B到地坐标系E的转换矩阵为

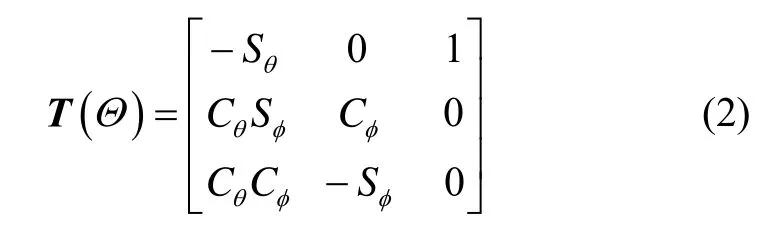
根据牛顿定律，定义在机体坐标系下的动力学方程为

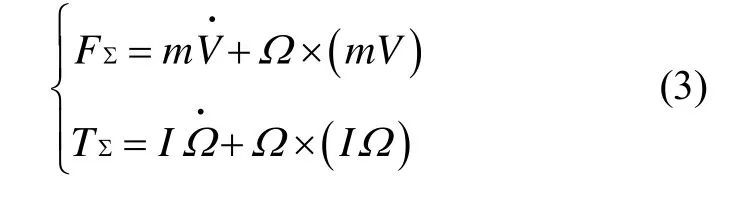
动力学模型的建立与控制率的设计，最终是为四旋翼操作者服务的。所以，站在地面的操作者所期望的输出，应为四旋翼在地面坐标系下平动和转动位移及其速率输出。为了实现对在机体坐标系B下所建四旋翼动力学方程向地面坐标系E下的转换，建立如下运动学方程：

为了简化计算，设定四旋翼在小角度下工作，因此可由式(1)～(4)，建立四旋翼牛顿-欧拉动力学方程，其状态空间表达式形式为

其中：l为螺旋桨中心与机体坐标系原点的距离；Ix,Iy,Iz为机体绕三轴的转动惯量；Jr为旋翼的转动惯量；A1,A2,A3,A4,A5,A6为各通道空气阻力（矩）；D1,D2,D3,D4,D5,D6为其未知干扰力（矩）；U1,U2,U3,U4是由螺旋桨转速决定的四个控制输入量；ωd为转速差值。具体如下：

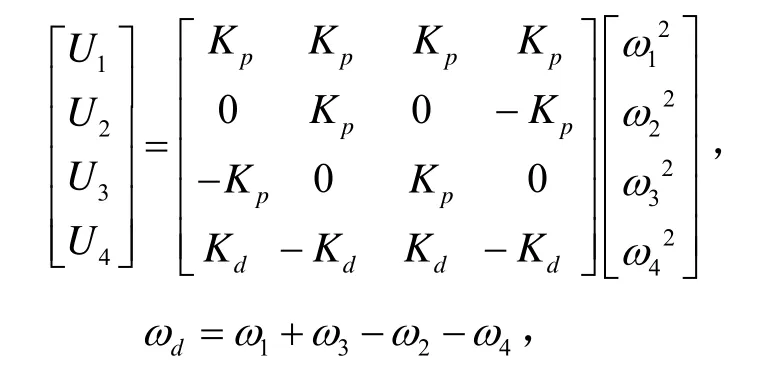
Kp、Kd分别为升力和拖拉系数，ωi为旋翼转速。

表1 四旋翼无人机螺旋桨升力与运动形式关系表Tab.1 Relationships between lift forces and movements

2 四旋翼无人机控制率的设计

四旋翼系统主要由平移和转动两个子系统组成。控制率设计的目标为：实现平移子系统下的位移轨迹追踪即P(x,y,z)→Pd(xd,yd,zd)；转动子系统姿态角追踪Θ(φ,θ,ψ)→Θd(φd,θd,ψd)。本文所设计控制率是按如下环节逐层设计，如图2所示。

图2 四旋翼无人机控制率设计流程图Fig.2 Procedure of control design for quadrotor

2.1 姿态控制器设计

考虑四旋翼无人机翻滚角通道二阶系统：

2.2 位置控制器设计

1）高度控制

同上述推导过程，控制输入U1为

2）水平控制

由式(5)可知，可取x、y虚拟控制输入ux和uy：

同上，则：

由式(13)可知，在给定目的偏航角值后，通过改变和控制姿态角的期望输出x3d、x1d即可实现需要的控制输入ux和uy，经过姿态角反解运算求得：

2.3 观测器设计

在所求各个控制率表达式中，含有未知干扰项D（实际中包括外部风力、负载变化、重心不平衡、参数未知等）。在此，通过设计和添加干扰观测器，无需额外的传感设备，即可实现控制率输入对干扰的实时补偿，保证四旋翼鲁棒飞行能力。

取翻滚角通道干扰观测器为

该观测器是用估计输出与实际输出的差值对估计值做修正。相对于观测器的动态特性，干扰D1的变化是缓慢的，即=0，则：

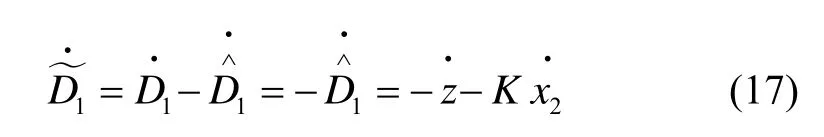
将式(16)中第二式代入式(17)，得：

因而得到的观测器观测误差方程为

观测误差为指数收敛稳定，式(19)解为

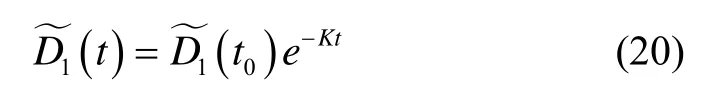
另外，取Lyapunov函数为

由式(18)和式(21)知，则其导数为

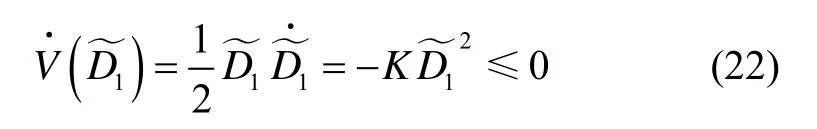
将式(23)代入式(6)，并令观测器指数收敛系数K取较大值，即观测器相对于控制系统为快变子系统，则有，参数k2、k1、1应满足多项式p2+k2p+k1为Hurwitz，其中p为Laplace算子。通过合理选取参数K、k1、k2的值，闭环控制系统即为指数收敛稳定。

其余 5个通道的观测器设计形式如式(16)，基于指数收敛控制器输入表达式形式如式(23)。

3 四旋翼无人机控制的仿真实验与分析

四旋翼飞行仿真试验中，分别对轨迹追踪、悬停和姿态控制飞行能力进行了实验设计与分析。

· 轨迹追踪：四旋翼无人机由起始点(0, 0, 0)开始垂

直起飞，5 s后到达(0, 0, 5)，以2 m为半径顺时针历时20 s匀速旋转一周，最后无人机从点(0, 0, 5)经过5 s返航至原点(0, 0, 0)。

· 悬停：在点(0, 0, 5)悬停。

· 姿态控制：姿态角φ、θ和ψ分别控制在 0.1、0.1和0rad。

针对四旋翼无人机飞行过程中常见问题添加相应干扰：考虑到机身配重不平衡，三个姿态角通道添加常值干扰；考虑到载重的连续性变化（如农药喷洒），高度通道添加斜坡函数干扰；考虑到无人机在平移过程中受到外部风扰动的影响，水平通道添加正余弦函数干扰。

四旋翼仿真结果如图3～6所示。

图3为指数收敛干扰观测器对外部未知干扰观测效果图，其中蓝色线为干扰实际值，红色线为估计值。从图3可以看出，所设计观测器对外部干扰具有较好的实时估计能力，增加了四旋翼无人机系统的稳定性与飞行的鲁棒性。

图4为四旋翼无人机轨迹追踪效果图，其中黑色线为所设定轨迹，红色线为线性反馈控制下的轨迹追踪，蓝色线为基于指数收敛观测器组合控制下的轨迹追踪。由图4可知，所设计的基于指数收敛的控制系统提高了轨迹追踪的精度及系统的稳定性，很好地满足了其鲁棒自适应飞行要求。

图5为悬停控制效果图，其中蓝色五角星所在位置为期望悬停点(0, 0, 5)，红色线为线性反馈控制下的悬停状态，蓝色线为基于指数收敛观测器组合控制下的无人机悬停状态。由图5可知，所设计的指数收敛观测器组合控制能够更好地保障旋翼无人机悬停的稳定性。

图3 干扰观测器观测效果图Fig.3 Effect of observer on estimating unknown disturbances

图4 四旋翼轨迹追踪图Fig.4 Trajectory tracking of quadrotor in 3D

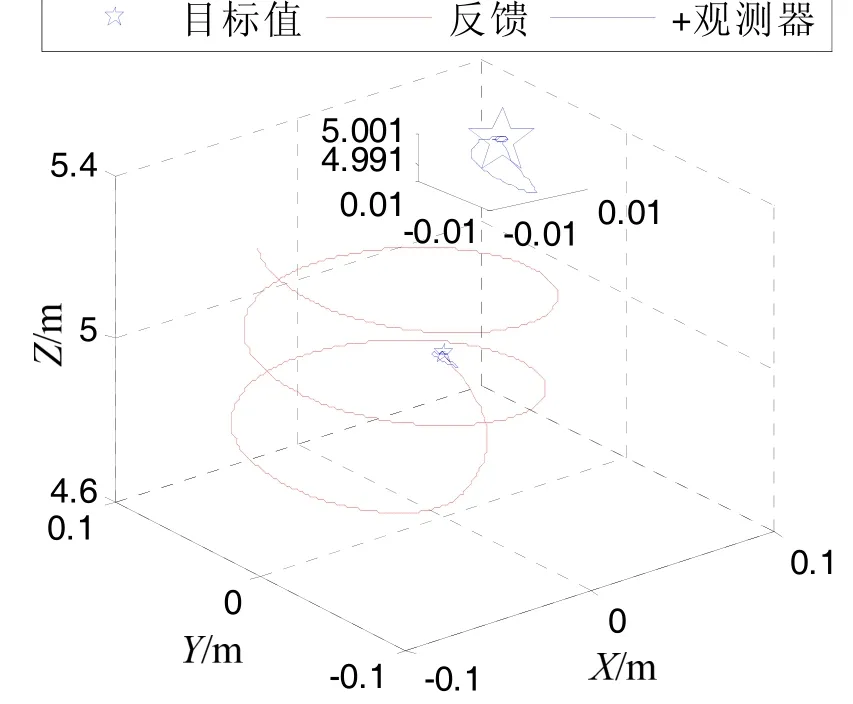
图5 悬停控制效果图Fig.5 Hover effect of quadrotor

图6为四旋翼无人机姿态控制效果图，其中黑色线为目的姿态角，红色线为线性反馈控制下的姿态追踪，蓝色线为基于指数收敛观测器组合控制下的姿态追踪。由图6可知，所设计基于指数收敛观测器组合控制能够实现无人机姿态角高精度追踪，提高了系统的鲁棒飞行能力。

图6 姿态追踪效果图Fig.6 Attitude tracking’s effect of quadrotor

4 结 论

本文基于牛顿-欧拉方程建立了四旋翼动力学模型，并将其分为转动和平动两个子系统。初步采用了线性化反馈控制器，解决了系统欠驱动、强耦合的非线性特性难题，实现了四旋翼无人机的基本飞行能力。在此基础上，针对四旋翼在实际飞行过程中存在的内外部位未知干扰，在线性化反馈控制基础上设计和添加了基于指数收敛的干扰观测器，它具有良好的干扰观测能力，并能实时对控制输入进行补偿，实现了四旋翼无人机的自适应鲁棒飞行能力。这种基于干扰观测器的鲁棒控制策略对于其它飞行器的抗干扰也具有较好的参考意义。

（References）：

[1] Wang Hong-yu, Zhao Jian-kang, Yu Wen-xian, et al. Modeling and position tracking control for quadrotor vehicle[J]. Journal of Chinese Inertial Technology, 2012, 20(4): 455-458.

[2] Salih A. Flight PID controller design for a UAV quadrotor[J]. Scientific Research and Essays, 2010, 23(5): 3660-3667.

[3] Diao C, Xian B, Zhang X, et al. An output feedback attitude tracking controller design for quadrotor unmanned aerial vehicles using quaternion[C]//Proceedings of the 2013 IEEE/RSJ International Conference on Intelligent Robots and Systems. Tokyo, Japan, 2013: 3051-3056.

[4] Basri M, Husain A, Kumeresan A. Enhanced backstepping controller design with application to autonomous quadrotor unmanned aerial vehicle[J]. Journal of Intelligent & Robotic System, 2015, 79(2): 295-321.

[5] Zheng En-hui. Second order sliding mode control for a quadrotor UAV[J]. Original Research Article ISA Transactions, 2014, 53(4): 1350-1356.

[6] 李劲松, 杨炼, 王乐天. 小型四旋翼无人直升机自适应优化控制[J]. 上海交通大学学报, 2015, 49(2): 202-208. Li Jin-song, Yang Lian, Wang Le-tian. Control of a small scale quad-rotor helicopter using adaptive control-optimization[J]. Journal of Shanghai Jiao Tong University, 2015, 49(2): 202-208.

[7] Lee D, Kim H, Sastry S. Feedback linearization vs. adaptive sliding mode control for a quadrotor helicopter [J]. International Journal of Control Automation and Systems, 2009, 7(3): 419-428.

[8] Alireza M, Mandi K. A novel nonlinear hybrid controller design for an uncertain quadrotor with disturbances[J]. Aerospace Science and Technology, 2015, 45(): 294-308.

[9] 陈彦民, 何勇灵, 孔令博, 等. 四旋翼飞行器分散 PID神经元网络控制[J]. 中国惯性技术学报, 2014, 22(2): 185-190. Chen Yan-min, He Yong-ling, Kong Ling-bo, et al. Decentralized PID neural network control for a quadrotor helicopter[J]. Journal of Chinese Inertial Technology, 2014, 22(2): 185-190.

[10] Heriberto R. Robust backstepping control based on integral sliding modes for tracking of quadrotors[J]. Journal of Intelligent & Robotic Systems, 2014, 73(1-4): 51-56.

[11] Efe M. Neural network assisted comupationally simple control of a quadrotor UAV[J]. IEEE Trans. Ind. Informat, 2010, 21(1): 50-66.

[12] Gautam D. Control of a quadrotor using a smart selftuning fuzzy PID controller[J]. International Journal of Advanced Robotic Systems, 2013, 10(5): 1-9.

[13] Escareno J. Trajectory control of a quadrotor subject to 2D wind disturbances[J]. Journal of Intelligent & Robotic Systems, 2013, 70(1-4): 51-63.

[14] 窦景欣, 孔祥希, 闻邦椿. 四旋翼无人机模糊自抗扰姿态控制及稳定性分析[J]. 中国惯性技术学报, 2015, 23(6): 824-830. Dou Jing-xin, Kong Xiang-xi, Wen Bang-chun. Attitude fuzzy active disturbance rejection controller design of quadrotor UAV and its stability analysis[J]. Journal of Chinese Inertial Technology, 2015, 23(6): 824-830.

Robust and adaptive flight control of quadrotor based on exponential convergence

ZHANG Ju-qian, REN Zhao-hui, ZHOU Lai-hong, WEN Bang-chun
(School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China)

A novel control algorithm based on exponential convergence is proposed for the flight control of quadrotor. Considering the under-actuated and strong coupled characteristics of quadrotor system, a feedback linearization control is adopted to realize its basic flight controls, such as trajectory tracking and hovering. In view that the feedback control is sensitive to the unknown inner and external disturbances existing in the system, an observer based on exponential trending law is designed to eliminate their adverse influence on the system. The adaptive and robustness flight of the quadrotor is realized by the proposed feedback control with observer. The hybrid control system realizes stable convergence based on exponential trending law. Simulation results show that the values of the disturbances can be perfectly estimated using the designed observer. The proposed hybrid control system is simple, and it has increased the stability of quadrotor in the presence of unknown disturbances, meeting the requirements of the quadrotor’s robust and adaptive flight performances.

quadrotor; trajectory tracking; feedback control; disturbance observer; exponential convergence; robust and adaptive

V249.1

：A

2016-04-21；

：2016-06-30

国家自然科学基金资助项目（51375080）；中央高校基本科研业务研究生科研创新项目（N1503060002）

张居乾（1988—），男，博士研究生，从事飞行器振动与控制方面的研究。E-mail: zhangjuqian@126.com

联 系 人：闻邦椿（1930—），男，教授，博士生导师，中国科学院院士。E-mail: bcwen1930@vip.sina.com

1005-6734(2016)04-0548-06

10.13695/j.cnki.12-1222/o3.2016.04.022