基于低频调制激励的硅微陀螺仪自动模态匹配技术

杨 成，李宏生，徐 露，朱昆朋

（1. 东南大学 仪器科学与工程学院，南京 210096；2. 东南大学 微惯性仪表与先进导航技术教育部重点实验室，南京 210096）

基于低频调制激励的硅微陀螺仪自动模态匹配技术

杨 成1,2，李宏生1,2，徐 露1,2，朱昆朋1,2

（1. 东南大学 仪器科学与工程学院，南京 210096；2. 东南大学 微惯性仪表与先进导航技术教育部重点实验室，南京 210096）

根据二阶质量-弹簧-阻尼系统的幅频特性和相频特性关于谐振频率对称的特点，提出了一种低频振荡激励的实时模态匹配技术，根据检测模态的输出响应来判别驱动模态和检测模态的匹配程度。首先简要介绍了带频率调谐功能的双质量线振动硅微陀螺仪，该陀螺利用负刚度效应来调节检测模态的谐振频率；然后通过理论推导以及系统仿真验证了基于低频调制激励的自动模态匹配技术的可行性和有效性；最后设计了一种基于现场可编程逻辑阵列（FPGA）的数字控制电路，并且对同一测试陀螺进行了模态匹配和模态不匹配下的性能对比。试验结果表明，相比模态不匹配条件下，陀螺零偏稳定性从5.89 (°)/h提高到1.26 (°)/h，角度随机游走从0.36 (°)/√h提高到0.079 (°)/√h，性能分别提高了4.7倍和4.6倍。

负刚度效应；硅微陀螺仪；低频振荡调制；模态匹配；自动频率调节

随着微机电（MEMS）技术的发展，越来越多的微传感器进入各种应用领域，其中，硅微陀螺仪作为MEMS技术的典型代表，具有集体小，成本低，易于批量生产，耐冲击等突出优点，使其在军用和民用领域有广泛的应用前景[1]。但目前受加工工艺等因素的制约，硅微陀螺仪的性能还不能满足高精度领域的应用要求。在现有加工工艺基础上提高硅微陀螺仪性能是本领域的重要课题。近年来，模态匹配成为研究热点，由于模态匹配可以极大提高陀螺结构的机械灵敏度，因此可以提高信噪比，改善陀螺的性能。模态匹配就是让陀螺的驱动模态和检测模态的自然频率趋于相等，由于加工的非理想因素以及环境温度的不确定性，很难保证实际工作频率与设计频率完全相等。因此，不少机构对频率调节的后加工技术进行了研究，比如激光微调技术[2]，带选择性的多晶硅沉淀技术[3]以及局部热应力技术[4]等。这些技术都需要人工调节，对结构会造成不可修复的损坏，而且由于温度的变化，导致输出也会出现不稳定。目前更流行、更有效的方法是利用结构特有的负刚度静电效应[5-7]，通过改变调谐直流电压来改变结构的刚度，从而改变陀螺结构的频率以达到模态匹配的目的。静电调节方式可以通过人工或者自动调节调谐电压的方式实现，可以利用模态匹配状态下的幅值和相位信息来判断模态匹配程度。文献[5-6]介绍了利用相位信息，基于锁相环控制，根据模态匹配下输入输出相移 90°的特性来判断模态匹配。文献[7]则利用响应信号的幅值信息，当模态匹配下，正交耦合信号的输出幅值最大。这两种方法只能在静态情况下进行频率调谐，当有角速度输入下，相位和幅值是变化的，无法完成实时模态匹配。

本文提出一种基于低频调制信号激励的实时模态匹配方案，利用课题组自主研制的带调谐电极的双质量线性振动硅微陀螺仪，通过在反馈梳齿上加载低频调制振荡信号，根据二阶质量-弹簧-阻尼系统的幅频特性和相频特性关于谐振频率对称的特点，通过比较频率响应来判别驱动模态和检测模态的匹配程度，从而达到实时模态匹配。

1 双质量线振动硅微陀螺仪频率调谐原理

带有频率调谐功能的双质量线性振动硅微陀螺结构示意图[8]如图1所示。该结构主要由三部分组成，分别是驱动框架、检测框架以及检测质量块。驱动框架和检测框架通过 U型梁达到解耦的目的，只沿 x轴或 y轴一个方向运动；检测质量块感应哥氏耦合力，具有双自由度，可沿x轴和y轴方向自由运动。利用压膜梳齿的静电负刚度效应[9]，在频率调谐电极施加直流电压可以改变检测框架的等效刚度，从而调节检测模态的谐振频率。调谐梳齿的局部细节图如图2所示，活动梳齿沿y轴运动。等效静电负刚度的表达式推导如下：

式中：n表示调谐梳齿的个数；h0为梳齿的厚度；d0为活动梳齿与固定梳齿之间的间距；l0为活动梳齿与固定梳齿之间重合的长度；ε为梳齿间的介电常数；Vdc为加载在活动梳齿与固定梳齿之间的直流调谐电压。

图1 双质量线振动硅微陀螺仪结构示意图Fig.1 Structural schematic of the dual-mass silicon MEMS gyroscope

图2 单个调谐梳齿电容结构示意图Fig.2 Structural schematic of the tuning comb-capacitor

因此，检测框架的等效刚度为

式中：kny为陀螺检测模态初始静电刚度。因此，直流调谐电压Vdc下的检测模态谐振频率表达式为

式中：my为检测质量块质量。

为了验证硅微陀螺仪的频率调谐特性，通过在调谐电极上施加不同的直流调谐电压，观察驱动和检测模态谐振频率的变化，实验结果如图3所示。检测初始谐振频率高于驱动谐振频率，驱动模态的谐振频率不受调谐电压的影响。检测模态的谐振频率随着电压的增加而减小，当电压为dc7.82V V=时，两模态的频率相同而达到模态匹配。

图3 调谐电压作用下驱动和检测模态谐振频率变化曲线Fig.3 Frequency tuning characteristics of drive mode and sense mode under the function of tuning voltage

2 基于低频调制激励的自动模态匹配工作原理

频率自动调节的原理图如图4所示，在陀螺检测反馈电极上施加一个调制信号，该调制信号是将低频振荡信号ωdem调制在与驱动位移同相位的信号ωd上，即得到ωd+ωdem和ωd-ωdem两个频率的双边激励信号。根据二阶质量-弹簧-阻尼系统的幅频和相频特性关于谐振频率具有对称性的特点，通过比较两个激励信号的响应来判别硅微陀螺仪驱动频率ωd与检测模态谐振频率ωy的匹配程度。

令驱动模态位移输出为x=Axcosωdt ，则哥氏力表达式为Fc=-2myΩzAxωdsin ωdt ，正交力表达式为正交力与驱动位移信号同相，哥氏力与驱动位移信号正交。在检测反馈电极施加调制力Fdem，它是将低频振荡信号调制在与驱动位移同相位的信号上。下面只考虑频率调节通道，等效调节环路如图5所示。

图4 检测模态自动频率调节控制框图Fig.4 Block diagram of automatic frequency tuning of the sense mode

图5 检测模态自动频率调节等效环路Fig.5 Equivalent loop of automatic frequency tuning of the sense mode

施加在陀螺检测反馈电极的等效调制力表达式为

式中：Adem为低频振荡信号的幅值；ωdem为低频振荡信号的频率；kvf为反馈静电力转换增益。因此，该调制力经过陀螺检测模态的电压响应输出为：

式中，kyv为检测接口位移/电压转换增益，其中，

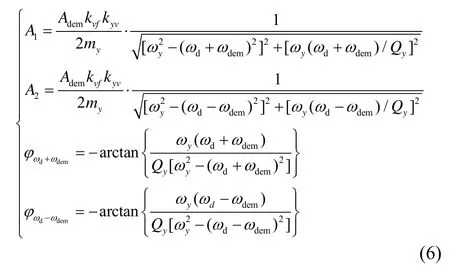
Vdem1进入速率解调通道，即被驱动位移参考信号解调，然后经过低通滤波得到输出：

随后，Vdem2进入频率控制通道，被低频振荡信号解调再经过低通滤波得到最终输出：

等式(8)即是检测通道模态匹配判断的表达式。将ωy=ωd+Δω代入式(8)，得到关于驱动模态和检测模态之间频差Δω的表达式：

为了让模态匹配，即Δω=0，代入上式(9)，得到基准控制电压Vref的值：

当陀螺结构和电路参数确定，式(10)中的各参量都是已知量，即能得到确定的基准控制电压值。

3 硅微陀螺仪模态自动匹配环路仿真与实验

3.1 仿真验证

硅微陀螺仪结构参数以及频率调节各环节的设计参数如表1所示。根据等式(9)绘制模态匹配判断信号关于频差的变化曲线，如图6所示。从图6可以发现，频差在-60Hz＜Δf＜60Hz 范围内，频率匹配点有唯一对应的电压值V(0)=0.0028V，这个电压值就是模态匹配控制环路的判断点。

表1 硅微陀螺仪和自动模态匹配模块设计参数Tab.1 Parameters of the silicon MEMS gyroscope and the mode-matching module

根据第2节图4介绍的自动模态匹配控制系统，在Simulink仿真系统中建立了整个控制模型，将表1给出的各个参数代入仿真模型中，分别得到陀螺系统输入输出响应曲线、检测模态频率变化曲线以及调谐电压变化曲线，如图7所示。从图7可以发现，经过一秒左右的调节时间，检测模态的谐振频率从初始3830 Hz最终稳定在驱动模态谐振频率3780 Hz，调节电压稳定在8.307 V，达到了模态匹配的效果。

图6 频率匹配判断信号与频差的变化关系Fig.6 Relationship between the distinguishing signal of mode-matching and the frequency difference

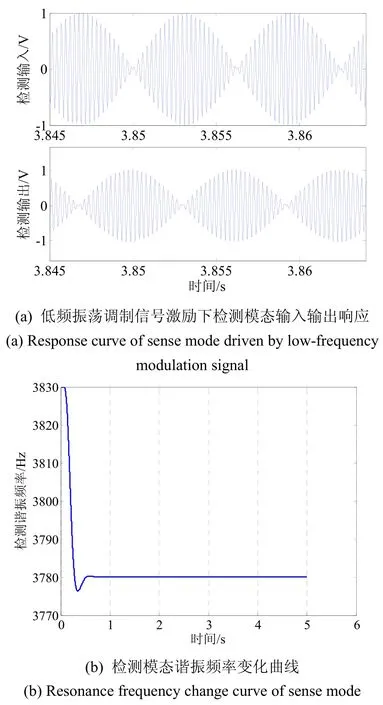
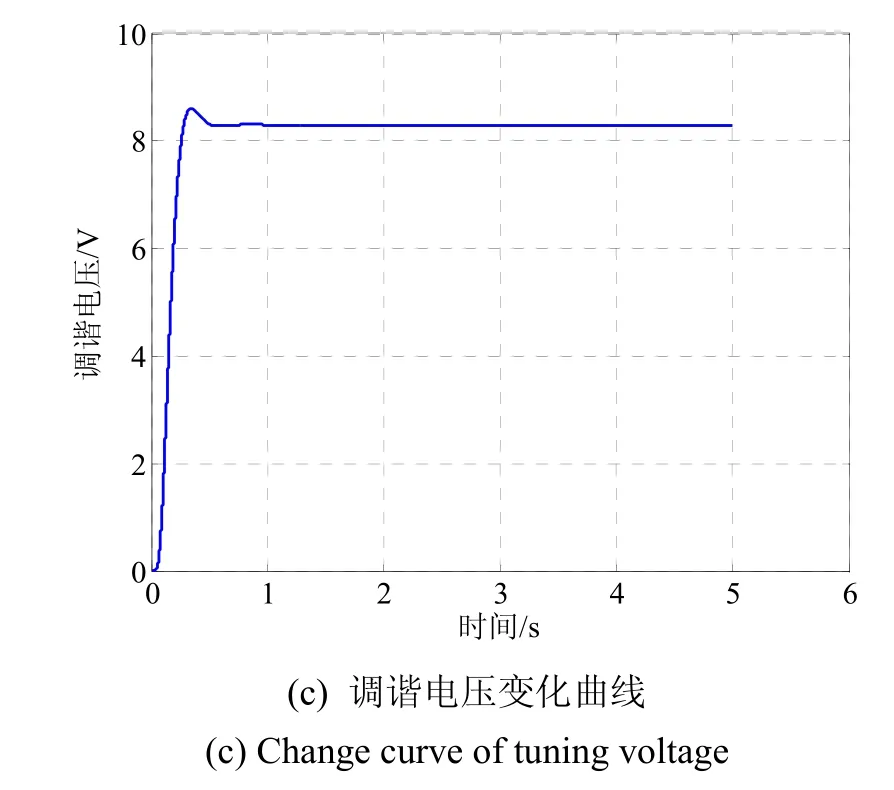
图7 自动模态匹配Simulink系统仿真图Fig.7 Simulation graph of the automatic mode-matching

3.2 实 验

为了进一步验证硅微陀螺仪自动模态匹配控制环路在实际系统的运行效果，设计了基于FPGA的电路控制方案，如图8所示。驱动环路以及前端解调电路已经在文献[10-11]进行了详细介绍，本文不再赘述。检测环路在原有开环检测的基础上添加了模态自动匹配控制环路。运用频率直接合成(DDS)技术，在检测反馈电极上施加一个低频振荡调制力，该调制力是将低频振荡信号调制在与驱动位移同相的参考信号上。调制力在检测模态的响应输出经过前端解调电路进入FPGA数字信号处理模块，将检测同相分量即速率通道的信号用低频振荡信号来解调，经过低通滤波后与参考电压合成作为频率调节环路控制器的输入信号，得到的输出经过D/A转换器，即得到最终的频率调谐电压，施加在硅微陀螺仪频率调谐电极上。

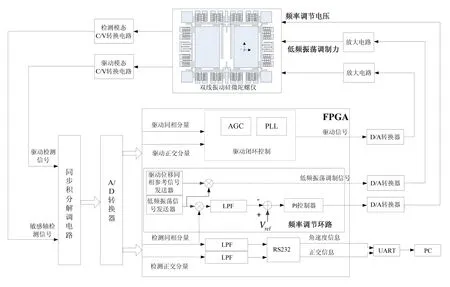
图8 硅微陀螺仪频率自动匹配数字控制方案Fig.8 Digital control scheme of automatic mode-matching of the silicon MEMS gyroscope

带自动模态匹配功能的陀螺数字控制系统与实验设备如图9所示。用示波器观察低频调制信号与检测响应信号，波形如图10所示。从图10可以发现其与仿真系统中模态匹配下的输入输出曲线图7(a)完全一致。为了验证模态匹配下硅微陀螺性能变化，分别在模态匹配以及模态不匹配(Vdc=0V)条件下对被测陀螺进行性能测试。标度因数变化曲线以及阿伦方差曲线如图11所示，并将被测陀螺的测试结果汇总于表2。从表2可以发现，相比模态不匹配条件下，陀螺标度因数从0.889 mV/(°/s)变为11.3 mV/(°/s)，零偏稳定性从5.89 (°)/h提高到1.26 (°)/h，角度随机游走从0.36 (°)/√h提高到0.079 (°)/√h，静态性能分别提高了4.7倍和4.6倍。

图9 陀螺测控电路及实验设备Fig.9 Circuit of the gyroscope and test equipments

图10 实际陀螺系统检测模态输入输出波形Fig.10 Actual waveform of response of sense mode driven by low-frequency modulation signal

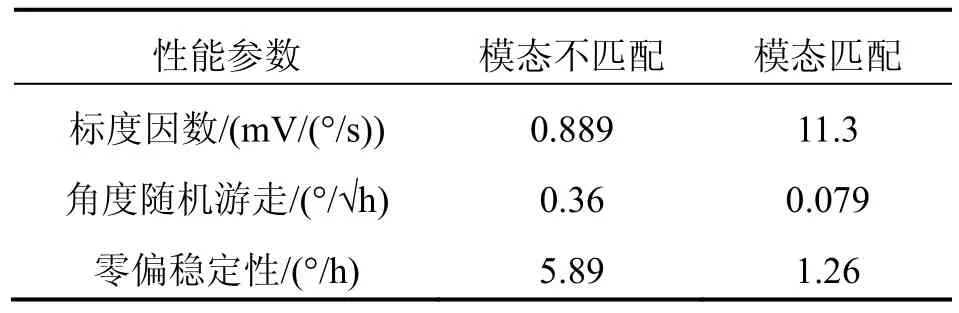
表2 被测陀螺测试结果Tab.2 Test results of the studied gyroscope

图11 被测陀螺分别在模态匹配和模态不匹配下的测试曲线Fig.11 Test curves of the studied gyroscope with mode-matching and mode-mismatching

4 结 论

本文根据二阶质量-弹簧-阻尼系统的幅频和相频特性关于谐振频率具有对称性的特点，提出了一种基于低频调制激励的实时模态匹配控制方案。通过理论推导、系统仿真以及实验验证，证明了该方案的可行性与有效性。该方案不仅在静态情况下切实可行，而且在有角速度输入下，频率自动调节环路也能正常工作，保证了陀螺在正常工作中的模态实时匹配。对测试陀螺进行了一系列的性能测试，相比模态不匹配条件下，陀螺零偏稳定性提高了4.7倍，角度随机游走提高了4.6倍，陀螺在模态匹配下的性能得到明显提高，为进一步提升陀螺精度提供了可行方案。下一步的工作将集中于模态匹配下的陀螺工作带宽拓展以及检测力反馈的设计。

（References）：

[1] 曹慧亮, 李宏生, 申冲, 等. 双质量硅微机械陀螺仪正交校正系统设计及测试[J]. 中国惯性技术学报, 2015, 23(4): 544-549. Cao Hui-liang, Li Hong-sheng, Shen Cong, et al. Structure model and system simulation of MEMS gyroscope [J]. Journal of Chinese Inertial Technology, 2015, 23(4): 544-549.

[2] Abdelmoneum M A, Demirci M M, Lin Y W, et al. Location-dependent frequency tuning of vibrating micromechanical resonators via laser trimming[C]//Proceedings of the 2004 IEEE International Conference on Frequency Control Symposium and Exposition. 2004: 272-279.

[3] Joachim D, Lin L. Characterization of selective polysilicon deposition for MEMS resonator tuning[J]. Journal of Microelectromechanical Systems, 2003, 12(2): 193-200.

[4] Remtema T, Lin L. Active frequency tuning for micro resonators by localized thermal stressing effects[J]. Sensors and Actuators A: Physical, 2001, 91(3): 326-332.

[5] Sung S, Sung W T, Kim C, et al. On the mode-matched control of MEMS vibratory gyroscope via phase-domain analysis and design[J]. IEEE/ASME Transactions on Mechatronics, 2009, 14(4): 446-455.

[6] Sonmezoglu S, Alper S E, Akin T. An automatically mode-matched MEMS gyroscope with wide and tunable bandwidth[J]. Journal of Microelectromechanical Systems, 2014, 23(2): 284-297.

[7] Sharma A, Zaman M F, Ayazi F. A sub-0.2 hr bias drift micromechanical silicon gyroscope with automatic CMOS mode-matching[J]. IEEE Journal of Solid-State Circuits, 2009, 44(5): 1593-1608.

[8] Xu Lu, Li Hong-sheng, Ni Yun-fang, et al. Frequency tuning of work modes in z-axis dual-mass silicon microgyroscope[J]. Journal of Sensors, 2014, 2014(3): 1-13.

[9] Sonmezoglu S, Alper S E, Akin T. An automatically mode-matched MEMS gyroscope with wide and tunable bandwidth[J]. Journal of Microelectromechanical Systems, 2014, 23(2): 284-297.

[10] Yang Cheng, Li Hong-sheng. Digital control system for the MEMS tuning fork gyroscope based on synchronous integral demodulator[J]. IEEE Sensors Journal, 2015, 15(10): 5755-5764.

[11] 杨成, 李宏生. 硅微陀螺仪驱动模态离散控制分析[J].中国惯性技术学报, 2015, 23(6): 780-785. Yang Cheng, LI Hong-sheng. Discrete control analysis on drive mode of silicon micromachined gyroscope[J]. Journal of Chinese Inertial Technology, 2015, 23(6): 780-785.

Automatic mode-matching technology for silicon MEMS gyroscope based on low-frequency modulation signal

YANG Cheng1,2, LI Hong-sheng1,2, XU Lu1,2, ZHU Kun-peng1,2
(1. School of Instrument Science and Engineering, Southeast University, Nanjing 210096, China; 2. Key Laboratory of Micro-Inertial Instrument and Advanced Navigation Technology of Ministry of Education, Southeast University, Nanjing 210096, China)

In view that the 2nd-order mass-spring-damper system has approximate symmetry resonance frequency characteristics, an automatic mode-matching technology driven by low-frequency modulation signal is presented. At first, the dual-mass silicon MEMS gyroscope with the function of frequency tuning is introduced, which uses the gyroscope’s negative stiffness effect to adjust the resonance frequency of the sense mode. Then, the automatic mode-matching technology of low frequency modulation is verified by theoretical derivation and system simulation. Finally, the digital control circuit based on field programmable logic array (FPGA) is designed, and the performances of the proposed gyroscope are tested under the mode-matching condition and mode-mismatching one, respectively. Experiment results demonstrate that the gyroscope’s performances under mode-matching condition are significantly improved compared with those under mode-mismatching condition, in which the bias instability is improved from 5.89 (°)/h to 1.26 (°)/h, and the angle random walk is improved from 0.36 (°)/√h to 0.079 (°)/√h, showing that the performances are improved by about 4.7 times and 4.6 times, respectively.

negative stiffness effect; silicon MEMS gyroscope; low-frequency modulation; mode-matching; automatic frequency tuning

U666.1

：A

2016-04-26；

：2016-06-30

江苏省科技支撑计划项目（BE2014003-3）；预研基金资助项目（9140A09011313JW06119）

杨成（1989—），男，博士研究生，从事微机械系统方面研究。E-mail: ycbb_yc@163.com

联 系 人：李宏生（1964—），男，教授，博士生导师。E-mail: hsli@seu.edu.cn

1005-6734(2016)04-0542-06

10.13695/j.cnki.12-1222/o3.2016.04.021