带有攻击角约束的多导弹协同制导律

宋俊红，宋申民，徐胜利

（1. 哈尔滨工业大学 控制理论与制导技术研究中心，哈尔滨 150001；2. 上海航天技术研究院 上海机动工程研究所，上海 201109）

带有攻击角约束的多导弹协同制导律

宋俊红1，宋申民1，徐胜利2

（1. 哈尔滨工业大学 控制理论与制导技术研究中心，哈尔滨 150001；2. 上海航天技术研究院 上海机动工程研究所，上海 201109）

针对带有攻击角约束的多导弹同时攻击机动目标问题，提出了一种带有攻击角约束的协同制导律。首先基于平面内的导弹-目标相对运动方程，建立了带有攻击角约束的协同制导模型；其次，把协同制导律的设计过程分离为两个部分：一是基于图论的有关内容，运用有限时间一致性理论设计沿着视线方向上的加速度指令来保证所有导弹与目标的相对距离在有限时间内到达一致，进而保证所有的导弹同时击中机动目标；二是利用非齐次干扰观测器对机动目标的加速度进行估计，并运用滑模控制设计视线法向上的加速度指令来保证每枚导弹与目标间的视线角速率收敛到零和视线角收敛到期望的终端视线角，即每枚导弹以期望的终端视线角成功击中目标；最后，对三枚导弹同时打击同一机动目标的情况进行仿真，仿真结果表明本文设计的带有攻击角约束的协同制导律的有效性和正确性。

协同制导律；攻击角约束；非齐次干扰观测器；滑模控制；通信拓扑；有限时间一致性

多导弹协同攻击以调整作战理念、适应未来环境为目的，打破作战过程中各导弹之间没有任何联系与合作的传统思想，将所有导弹看作一个整体，多导弹之间通过信息共享实现配合、协作，共同完成打击任务，极大地提高了导弹的杀伤力和突防能力，而且能够完成单枚导弹无法完成的任务，因此研究多导弹协同攻击具有非常重要的实际意义。

文献[1]提出了一种攻击时间可控的多导弹时间协同制导律，该制导律是在比例制导律基础上附加攻击时间的误差反馈，但是该制导律需要事先指定攻击时间，然后各枚导弹单独采用该制导律进行指导，完成同时攻击的目的。文献[2]提出了一种基于虚拟领弹的带有时间限制的多导弹协同制导的方法，是将攻击时间同时达到问题转化为各枚导弹-虚拟领弹的弹目相对距离和前置角的跟踪问题，从而使各枚被领弹都按照虚拟领弹的指定攻击时间同时攻击目标，实现多导弹时间协同导引。文献[3]基于动态面控制理论和干扰观测器技术研究了制导与控制一体化的多导弹协同打击目标问题。文献[4-5]基于滑模控制方法提出带有攻击时间控制的制导律。以上文献所提出的协同制导方法针对的都是静止的目标，而且需要人为地事先指定攻击时间，还有在制导过程中各导弹之间没有动态的信息交互，不能实现真正意义上的导弹协同。

为了实现真正意义上导弹协同，文献[6]基于分布式协同制导方法，分别设计了分散化协同制导律和分布式自适应协同制导律，实现多导弹协同攻击。文献[7]研究了固定拓扑和切换拓扑两种情况下同时存在通信时延和拓扑结构不确定的多导弹协同齐射攻击问题。文献[8]研究了切换拓扑下存在通信时延的基于领弹-从弹的多导弹协同制导的一致性问题。以上多导弹协同攻击的目标也都是静止的。针对多导弹协同攻击机动目标的研究还比较少[9-12]，文献[9-10]在各导弹之间不存在信息交互下的情况下设计的多导弹协同制导律，文献[11-12]研究了在以通信拓扑结构形式来表示导弹之间的信息交互下，提出攻击机动目标的协同制导律。

目前，国内外学者针对多导弹存在信息交互并协同攻击机动目标的问题研究还非常有限，尤其是带有攻击角约束[13]的多导弹协同攻击机动目标问题。在多导弹同时攻击目标时以不同或相同的攻击角击中目标，不仅能够提高导弹的突防能力，而且还有进一步提高导弹的杀伤力和全方位的攻击能力。所以，本文基于有限时间一致性理论和滑模控制理论，提出了带有攻击角约束的多导弹协同攻击机动目标的协同制导律，同时满足各导弹之间具有动态的信息交互和各导弹以所期望的攻击角同时击中目标。基于协同制导模型，文中设计的协同制导律分为两个部分：一是基于非齐次干扰观测器和滑模控制设计视线法向上的加速度指令来保证每枚导弹与目标间的视线角速率收敛到零，即每枚导弹成功拦截，并且满足指定的攻击角约束；二是运用有限时间一致性理论设计沿着视线方向上的加速度指令来保证所有导弹同时击中机动目标。最后进行仿真验证协同制导律的有效性。

1 协同拦截的问题描述

针对平面拦截问题，导弹与目标的相对运动几何关系如图1所示，其中M和T分别表示导弹和目标的质心，r代表导弹和目标之间的相对距离，q代表视线角， φm、 φt分别代表导弹和目标的速度方向角，Vm、Vt分别代表导弹和目标的速度。由图1可导出导弹与目标的相对运动方程[14]为

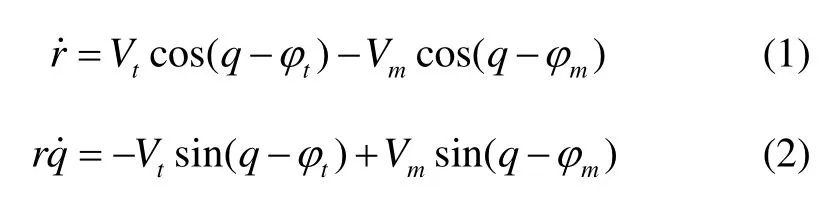
图1 单枚导弹与目标的相对运动关系Fig.1 Relative motion of a single missile and the target

对式(1)和(2)分别对时间求导，得到：

式中：ur和wr分别是导弹加速度和目标加速度在视线方向上的分量；uq和wq分别是导弹加速度和目标加速度在视线法向上的分量。在末制导过程中，目标主要在视线法向上进行机动，因此，可以假设目标加速度在视线方向的分量为零，即wr=0。

其中，qd是期望的终端视线角，可获得：

图 2给出了多枚导弹与目标的相对运动几何关系，每枚导弹的初始条件可以不同。带有角度约束的协同拦截目地是针对每枚导弹设计制导律，使得所有的导弹在分布式的通信拓扑下同时击中机动的目标，并且视线角达到期望的终端视线角。正如图 2所示的，每枚导弹的状态用对应下标i(i=1,2,…,n)表示，第i枚导弹与目标的相对运动方程表示为

基于以上分析，由式(6)可知，在多导弹攻击单一目标的协同制导问题中，协同制导律的设计过程可以分成两部分：通过设计视线法向上的加速度指令uqi使弹目相对距离收敛，即使得每枚导弹的视线角收敛到期望的终端视线角和视线角速率收敛到零；通过设计视线方向上的加速度指令uri，使得多枚导弹与目标的相对距离在有限时间内到达一致，即ri→rj，进而保证多导弹同时击中目标。

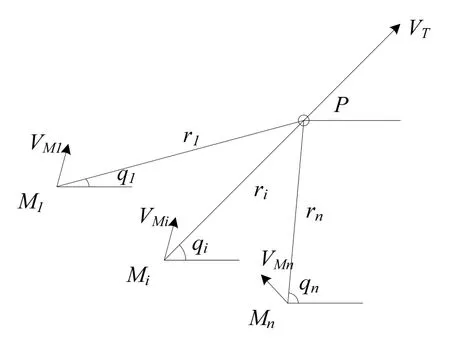
图2 多枚导弹与目标的相对运动关系Fig.2 Relative motion of the missiles and the target

注 1 传统的末制导律设计只是通过设计视线法向的加速度指令保证视线角速率收敛到零。这是因为导弹目标相对速度的变化率是很小的，并且初始的相对速度比零小很多，沿着视线方向的加速度指令通常被设定为零。但是，为了使得导弹与目标的相对距离在有限时间内到达一致，来达到同时攻击目标的目的，视线方向的加速度指令应该被设计。

注 2 设计视线方向上的加速度指令需要考虑有限时间一致性，而不是渐进一致性，这是因为每枚导弹相对于目标的相对距离应该在导弹目标碰撞时间前达到一致。

2 协同制导律设计

2.1 视线方向上的加速度指令设计

在本小节中，基于二阶多智能体系统有限时间一致性原理设计了视线方向上的加速度指令，来保证所有的导弹同时击中机动目标。

在多导弹协同制导中，导弹通过信息交互获得其它导弹的状态信息以完成多导弹协同一致性问题，这种信息交互可以通过图论来描述。下面简单介绍一下图论的基础知识。

在本文中，用无向图G=(v,ζ,C)来代表多导弹之间的通讯拓扑关系，其中v描述图中节点组成的集合，ζ代表节点之间的连线，矩阵C=[cij]∈Rn×n代表权系数矩阵，节点vi代表第i枚导弹。图G中的任意边可以描述为(vi,vj)，其中(vi,vj)代表无序节点对，若第i枚导弹和第 j枚导弹之间能够进行信息交换，则，否则cij=0，特别的cii=0, i∈{1,2,…,n}，由于G是无向图，有cij=cji。若节点vi和节点vj之间存在一条通道，则通路上连续的节点都是相邻的。如果无向图中任意两个节点间都存在至少一条通路，则整个图是连通的。

在设计视线方向上的加速度指令之前，先给出了一个关于二阶多智能体系统有限时间一致性收敛的引理。考虑如下二阶多智能体系统：

式中，xi表示位移，vi表示速度，ui表示控制输入，初始条件为xi(0)=xi0，vi(0)=vi0。

引理 1[15]考虑具有n个个体的多智能体系统(7)，在其通信拓扑结构图G无向且连通时，设计有如下控制输入：

上述引理给出了二阶多智能体系统有限时间一致性收敛的充分条件。基于上述引理，针对式(6)中前两个方程描述的子系统：

通过设计uri来控制所有的导弹与目标的相对距离在有限时间内到达一致，即 ri→rj，以实现多导弹同时拦截。下面以定理的形式给出视线方向上的制导律设计。

定理 1 针对系统(9)，在其通信拓扑结构图G无向且连通时，那么视线方向上的加速度指令uri设计为

证明：定理1的证明很容易由引理1得到。

2.2 视线法向上的加速度指令设计

在本小节中，基于滑模控制和非齐次干扰观测器来设计视线法向上的加速度指令，使每枚导弹的视线角收敛到期望的终端视线角和视线角速率收敛到零，既保证每枚导弹能够以期望的视线角成功拦截目标。

考虑式(6)中后两个方程描述的子系统如下：

针对式(11)所示的带有角度约束的制导系统，通过对每枚导弹的视线法向上的加速度指令uqi进行设计来保证每枚导弹与目标间的视线角速率收敛到零和视线角收敛到期望的终端视线角。

注 1[16]在制导过程中，弹目相对距离 r满足

iri0≤ri≤ri(0)，其中ri0是导引头存在的最小作用距离，ri(0)代表弹目相对距离的初始值。

在实际的制导过程中，如果目标进行机动，其机动加速度是个很难获得量，把它视为系统的外界干扰，但在制导过程中是有界量。于是有下面的假设：

为了消除带有角度约束的制导子系统(11)中由于目标机动带来的外界总干扰di(t)，利用文献[17]提出的有限时间收敛的非齐次干扰观测器来估计系统(11)式中的外界总干扰。针对制导子系统(11)，通过设计以下形式的非齐次干扰观测器(12)来估计外界总干扰。

对于带有角度约束的制导子系统(11)，在外界干扰存在的情况下，设计视线法向上加速度指令uqi使得视线角速率渐进收敛到零和终端视线角渐进收敛到期望的攻击角。同一般的滑模控制方法设计相似，首先是设计滑模面，来获得所期望的控制效果。则选取如下线性滑模面：

式中，ki＞0为设计常数。

为了让制导系统状态快速地从初始状态收敛到滑模面(13)，选取以下的快速幂次趋近律：

式中，k1i,k2i＞0，0＜ρi＜1。

在描述定理之前，先给出如下的引理。

引理2[18]假设存在连续、正定函数V(t)满足如下的微分不等式：

式中，α,β＞0，0＜γ＜1均为常数，那么系统状态将在有限时间内收敛到平衡点。到达平衡点的时间tf满足下面不等式：

下面给出视线法向上的制导律设计。

定理2 针对带有角度约束的制导子系统(11)，如果滑模面设计为式(13)，趋近律选为式(14)，以及利用非齐次干扰观测器(12)式对子系统(11)中外界总干扰进行估计，在以下设计的视线法向上的加速度指令(17)的作用下，滑模面在有限时间内收敛到零。进而可得视线角速率指数收敛到零，视线角qi指数收敛到期望的终端视线角qdi，即实现导弹以期望的攻击角精确命中目标。

证明：选取如下Lyapunov 函数

对Vi求导，并将式(11)(13)(17)代入其中，可得：

由引理2可得，滑模面si在有限时间内收敛到零。

在滑模面si=0上，，即解得，从而即视线角qi(t)指数收敛到期望的终端视线角qdi，且

即视线角速率也指数收敛到零，证毕。

3 仿真分析

为了验证本文所提出的带有角度约束的协同制导律(10)和(17)的有效性，下面考虑三枚导弹同时攻击一个机动目标的情形，进行仿真验证。目标的初始位置为(0m,0m)，速度为1700 m/s，初始航向角0°，目标加速度为2

30cos(t)m/s。三枚导弹的初始条件如表 1所示，各导弹可用过载为30g，g=9.8 m/s2。仿真步长取0.001 s。

三枚导弹之间的通信网络如图 3所示，该通信网络是连通的，且对应的权系数矩阵可以描述为

图3 三枚导弹之间的通信拓扑Fig.3 Communication topology among three missiles

非齐次干扰观测器(12)的参数取为： λ0i=1.1，λ1i=1.5，λ2i=2，μ0i=3，μ1i=6，μ2i=8， Li=100，其中，i=1,2,3。

沿视线方向的加速度指令(10)的参数选取如下：函数φk取为φk(x)=x，(k =1,2)；γ1=0.6，γ2=3/4。

视线法向上的加速度指令(17)参数取为：ki=1，k1i=6，k2i=2，ρi=2/3。

表1 导弹的初始条件Tab.1 Initial conditions of the missile

本文所设计的带有角度约束的协同制导律(10)和(17)作用下的仿真结果如图4～图8和表2所示。

表2 脱靶量、制导时间和角度误差Tab.2 Miss distance, guidance time and angle error

由表2可见，三枚导弹都以较小的脱靶量0.0774 m精确命中目标，并且制导时间一致，从而保证了三枚导弹同时击中目标，并且都以期望的末端视线角打击目标，角度误差不超过0.002°。

从图4可以看到，在协同制导律的作用下，各导弹的弹目相对距离由不同的初始值逐渐趋于一致，大约在7 s时达到一致，并且最后收敛到零，从而使表2中显示的三枚导弹最终在25.77 s时同时击中机动目标。

图4 弹目相对距离Fig.4 Relative distance between missile and target

图5显示了3枚导弹视线方向的加速度指令曲线，由图可见，三枚导弹的加速度曲线在初始阶段有弯曲，这是为了调整 3枚导弹的弹目相对距离快速趋于一致，实现对机动目标的快速协同攻击，当弹目相对距离趋于一致后，过载曲线很快趋于一致并收敛到零。

图5 视线方向加速度指令Fig.5 Acceleration commands in line-of-sight direction

图6为导弹的视线法向上的加速度指令曲线，为了能够使视线角速率收敛到零，制导初期加速度值比较大，但随着视线角速率收敛到零加速度变的平缓并趋于零附近。

图6 视线法向加速度指令Fig.6 Acceleration commands in line-of-sight’s normal direction

由图7可见，相应的视线角速率曲线也较弯曲，但随着弹目距离的接近，视线角速率曲线快速变小趋于零，这保证了导弹能精确命中目标。

图8为三枚导弹相应的视线角曲线，可见都收敛到相应的期望值。

从图4～图8和表2可以看出，本文所提出的带有攻击角约束的协同制导律能够产生非常好的制导性能，而且应该指出设计视线方向上加速度指令来实施协同攻击是很有必要的。

图7 视线角速率Fig.7 Line-of-sight angle rate

图8 视线角Fig.8 Line-of-sight angle

4 结 论

本文针对多导弹同时攻击同一机动目标，并且以一定的期望攻击角击中目标问题进行了研究，基于带有角度约束的协同制导模型，设计了一种带有角度约束的协同制导律。协同制导律的设计过程分为两方面分别设计：一是运用有限时间一致性理论设计了沿着视线方向上的加速度指令来保证所有的导弹同时击中机动目标；二是利用非齐次干扰观测器和滑模控制理论设计视线法向上的加速度指令来保证每枚导弹都能以期望的攻击角成功击中目标。针对三枚导弹同时打击同一目标机动目标情况，仿真结果验证了所设计的带有角度约束的协同制导律的有效性。

（References）：

[1] Jeon I S, Lee J I, Tahk M J. Impact-time-control guidance law for anti-ship missiles[J]. IEEE Transactions on Control Systems Technology, 2006, 14(2): 260-266.

[2] Zhao S Y, Zhou R, Wei C, et al. Design of timeconstrained guidance laws via virtual leader approach[J]. Chinese Journal of Aeronautics, 2010, 23(1): 103-108.

[3] Wang X F, Zheng Y Y, Lin H. Integrated guidance and control law for cooperative attack of multiple missiles[J]. Aerospace Science and Technology, 2015, 42: 1-11.

[4] Kumar S R, Ghose D. Sliding mode control based guidance law with impact time constraints[C]//American Control Conference. 2013: 5760-5765.

[5] Cho D, Kim H J, Tahk M J. Nonsingular sliding mode guidance for impact time control[J]. Journal of Guidance, Control, and Dynamics, 2016, 39(1): 61-68.

[6] 邹丽, 孔繁峨，周锐. 多导弹分布式自适应协同制导方法[J]. 北京航空航天大学学报，2012, 38(1): 128-132. Zou Li, Kong Fan-e, Zhou Rui. Distributed adaptive cooperative guidance for multi-missile salvo-attack[J]. Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(1): 128-132.

[7] 王青, 后德龙, 李君, 等. 存在时延和拓扑不确定的多弹分散化协同制导时间一致性分析[J]. 兵工学报，2014, 35(7): 982-989. Wang Qing, Hou De-long, Li Jun, et al. Consensus analysis of multi-missile decentralized cooperative guidance time with time-delays and topologies uncertainty[J]. Acta Armamentarll, 2014, 35(7): 982-989.

[8] Sun X J, Zhou R, Hou D L, et al. Consensus of leaderfollowers system of multi-missile with time-delays and switching topologies[J]. Optik, 2014, 125: 1202-1206.

[9] 周锐, 孙雪娇, 吴江, 等. 多导弹分布式协同制导与反步滑模控制方法[J]. 控制与决策, 2014, 29(9): 1617-1622. Zhou Rui, Sun Xue-jiao, Wu Jiang, et al. Multi-missile distributed cooperative guidance integrating backstepping sliding mode control[J]. Control and Decision, 2014, 29(9): 1617-1622.

[10] Guo C, Liang X G. Cooperative guidance law for multiple near space interceptors with impact time control [J]. International Journal of Aeronautical and Space Sciences, 2014, 15(3): 281-292.

[11] Zhang P, Liu H T, Li X B. Fault tolerance of cooperative interception using multiple flight vehicles[J]. Journal of the Franklin Institute, 2013, 350(9): 2373-2395.

[12] Shaferman V, Shima T. Cooperative optimal guidance laws for imposing a relative intercept angle[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(8): 1395-1408.

[13] 周慧波, 宋申民, 刘海坤. 具有攻击角约束的非奇异终端滑模导引律设计[J]. 中国惯性技术学报, 2014, 22(5): 606-618. Zhou Hui-bo, Song Shen-min, Liu Hai-kun. Nonsingular terminal sliding mode guidance law with impact angle constraint[J]. Journal of Chinese Inertial Technology, 2014, 22(5): 606-611.

[14] 宋俊红, 宋申民. 考虑输入受限和自动驾驶仪延迟的自适应滑模制导律[J]. 中国惯性技术学报, 2015, 23(3): 339-344. Song Jun-hong, Song Shen-min. Adaptive sliding mode guidance law with input constraints and autopilot lag[J]. Journal of Chinese Inertial Technology, 2015, 23(3): 339-344.

[15] Wang X, Hong Y. Finite-time consensus for multi-agent networks with second-order agent dynamics[C]//Proceedings of the IFAC World Congress, 2008: 15185-15190.

[16] He S M, Lin D F, Wang J. Robust terminal angle constraint guidance law with autopilot lag for intercepting maneuvering targets[J]. Nonlinear Dynamics, 2015, 81: 881-892.

[17] Li P, Peng X F, Ma J J, et al. Non-homogeneous disturbance observer-based second order sliding mode control for a tailless aircraft[C]//Proceedings of Chinese Automation Congress. 2013: 120-125.

[18] Song J H, Song S M. Three-dimensional guidance law based on adaptive integral sliding mode control[J]. Chinese Journal of Aeronautics, 2016, 29(1): 202-214.

Cooperative guidance law for multiple missiles with impact angle constraints

SONG Jun-hong1, SONG Shen-min1, XU Sheng-li2
(1. Center for Control Theory and Guidance Technology, Harbin Institute of Technology, Harbin 150001, China; 2. Institute of Shanghai Academy of Spaceflight Technology, Shanghai Electro-mechanical Engineering Institute, Shanghai 201109, China)

To solve the problem in multiple missiles attacking a maneuvering target simultaneously, a novel cooperative guidance law with impact angle constraints is proposed. At first, based on missile-target relative motion equation in plane, the cooperative guidance model with impact angle constraints is constructed. Then, the process of cooperative guidance law design is divided into two parts. In the first part, with the use of the graph and finite-time consensus theory, the acceleration command on the LOS direction is developed to guarantee that all relative distances from the missile to the target reach the agreement in finite time, and all missiles reach the maneuvering target simultaneously. In the second part, based on the sliding mode control and the non-homogeneous disturbance observer employed to estimate the acceleration of the maneuvering target, the acceleration command along the normal direction of the line-of-sight (LOS) is designed to guarantee that the LOS angular rate between each missile and the target converges to zero and the LOS angle converges to the desired terminal LOS angle. Thus every missile can successfully hit the target with the desired terminal LOS angle. Finally, simulation results for the interception scenario of three missiles intercepting a maneuvering target are provided, which demonstrate the effectiveness and superiority of the proposed cooperative guidance law with impact angle constraints.

cooperative guidance law; impact angle constraints; non-homogeneous disturbance observer; sliding mode control; communication topology; finite-time consensus

V448.133

：A

2016-04-12；

：2016-07-27

航空科学基金（20140177002）；上海航天科技创新基金（SAST201402）；国家自然科学基金创新群体项目（61021002）

宋俊红（1987—），女，博士研究生。E-mail: hitsjh@163.com

联 系 人：宋申民（1968—），男，教授，博士生导师，研究方向为非线性系统的稳定性分析、鲁棒控制、导弹制导与飞行器控制。E-mail: songshenmin@hit.edu.cn

1005-6734(2016)04-0554-07

10.13695/j.cnki.12-1222/o3.2016.04.023