遥操作主手机器人精度标定研究*
2016-01-22罗继曼李根标
罗继曼,李根标
(沈阳建筑大学 机械工程学院,沈阳 110168)
遥操作主手机器人精度标定研究*
罗继曼,李根标
(沈阳建筑大学 机械工程学院,沈阳110168)
摘要:为了提高遥操作主手并联机器人的运动精度,提出了一种利用激光检测仪和最小二乘解对并联机器人进行精度标定的研究方法。通过机构运动过程中的闭环链识别出有效的参数误差源,利用机器人的运动学正解方程构造误差的Jacobian矩阵。其方法是,首先通过激光检测仪测量出运动过程中末端执行部件的实际位置;其次采用最小二乘法对构造的误差Jacobian矩阵进行求解,识别出误差参数,将误差补偿到理论运动学模型中求解包含误差的末端执行部件的位置,将标定前后的值与理论值进行对比;最后通过定位精度、标准误差、均方根误差等性能评价指标检验标定结果;结果显示,标定后的定位精度比之前提高了65%,标准误差比之前提高了79.47%,机构的绝对定位精度和稳定性得到提高。
关键词:遥操作主手机器人;激光检测仪;最小二乘法;标定技术
0引言
遥操作主人是一台具有空间3平移自由度通常应用于医学领域和航天领域的高精密小型机器人。其通过人对主手机器人的控制,来实现从手的远程动作。主手的运行精度直接影响了从手的工作,因为对主手机器人进行运动学标定,使其运动精度满足实际工况的需要显得尤为重要。运动学标定的基本原理是,利用闭链约束和误差可观性,构造实测信息与模型输出间的误差传递函数,并用非线性最小二乘法计算识别出的误差值,将误差结果带入控制器中的逆解模型参数进行修正,进而达到精度补偿的目的。其通常可以分为4个部分:系统建模、参数辨识、误差测量和误差补偿。
机器人标定的目的在于提高机器人在加工过程中的绝对精度,保证加工质量。目前在机器人标定方面国内外很多学者对其进行了深入而广泛研究。文献[1]在对Hexapod进行标定的过程中分析了使用牛顿迭代法和最小二乘法之间的区别,使得在求解过程中能够减少计算量得到高精度的解;文献[2-4]提出了利用最小二乘近似的标定算法,并给出了包含结构误差项的运动学模型;文献[5-6]研究了模型的复杂性对机器人精度的影响,论述了误差对运动学精度的影响;他们的研究表明,非几何误差只有在无法达到所需的精度要求时才加以考虑;文献[7]考虑了标定时测量的系统误差对标定结果的影响,将并联机器人的基准参考坐标系变换到测量仪器的基准坐标系中,改进并联机器人的标定建模方式,克服了测量数据的基准与并联机器人的基准不统一的问题。
本文通过采用标定技术分析出影响机器人精度的关键因素,并利用最小二乘法识别出参数误差,从而有效的对精度进行补偿。
1遥操作主手标定模型介绍
本文自主研发了遥操作主手机器人对并联Delta构型工业机器人进行分析。其结构由3个半圆盘(在此可视为主动杆)和3条从动杆组成的相互对称的结构,并联机构整体上具有行X、Y、Z三个方向的平动;其运动学通常通过D-H坐标变换构造封闭链,利用矢量合成进行计算。通过得到运动学方程,在识别出的误差的基础上建立相应的误差补偿模型。
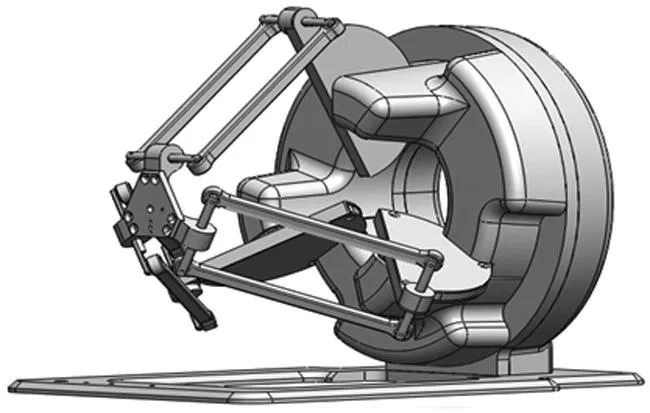
图1 三自由度并联机器人模型
由于机构的3条支链都是相互对称的机构,故可以将其运动学写成通式的形式,其运动学模型:以红线部分构造闭环建立方程为例:
Li=(xp+xi)2+(yp+yi)2+(zp+zi)2
(1)
xi,yi,zi—并联机器人铰链点的位置参数和姿态参数。
将式(1)变换为通式的形式:
Li=fi(X,U,R)X=(xpypzp)
(2)
其中:X=(xpypzp)代表末端的位置矩阵;U为铰链点坐标矩阵,R为铰链的夹角矩阵。i=1,2,3代表3杆的位姿,对式(2)两边求全微分,可得并联机器人的误差关系表达式:
(3)
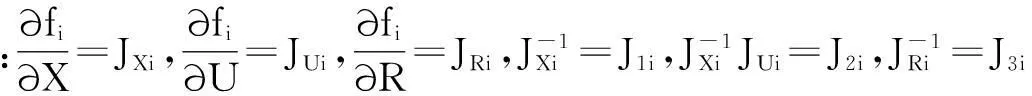
(4)
式(4)中dX—实际输出与名义输出间的位置误差矩阵,dLi—杆长在实际运动过程中受压力和热变形等外界因素引起的误差矩阵;dU—在生产和安装过程中,铰点位置变化引起的结构误差矩阵;J1i,J2i,J3i—并联机器人的固定平台姿态参数的名义值与实际值的误差矩阵;J1i,J2i,J3i—其各个误差矩阵所对应的系数矩阵。模型的优点在于既考虑了结构参数和姿态参数在实际加工过程中造成的误差,又将在并联机器人运动过程中内部作用力和外部环境所造成的误差加以考虑,避免了误部分随机误差的影响。本文在第3节介绍在利用此模型的优点的基础上,在初始标定的过程中,消除了部分误差的影响,将误差采用新的方式进行补偿,避免了一些复杂的求解过程,所以本文的研究在一定程度上具有利用的价值。
2标定过程
2.1并联机器人模型机构简化
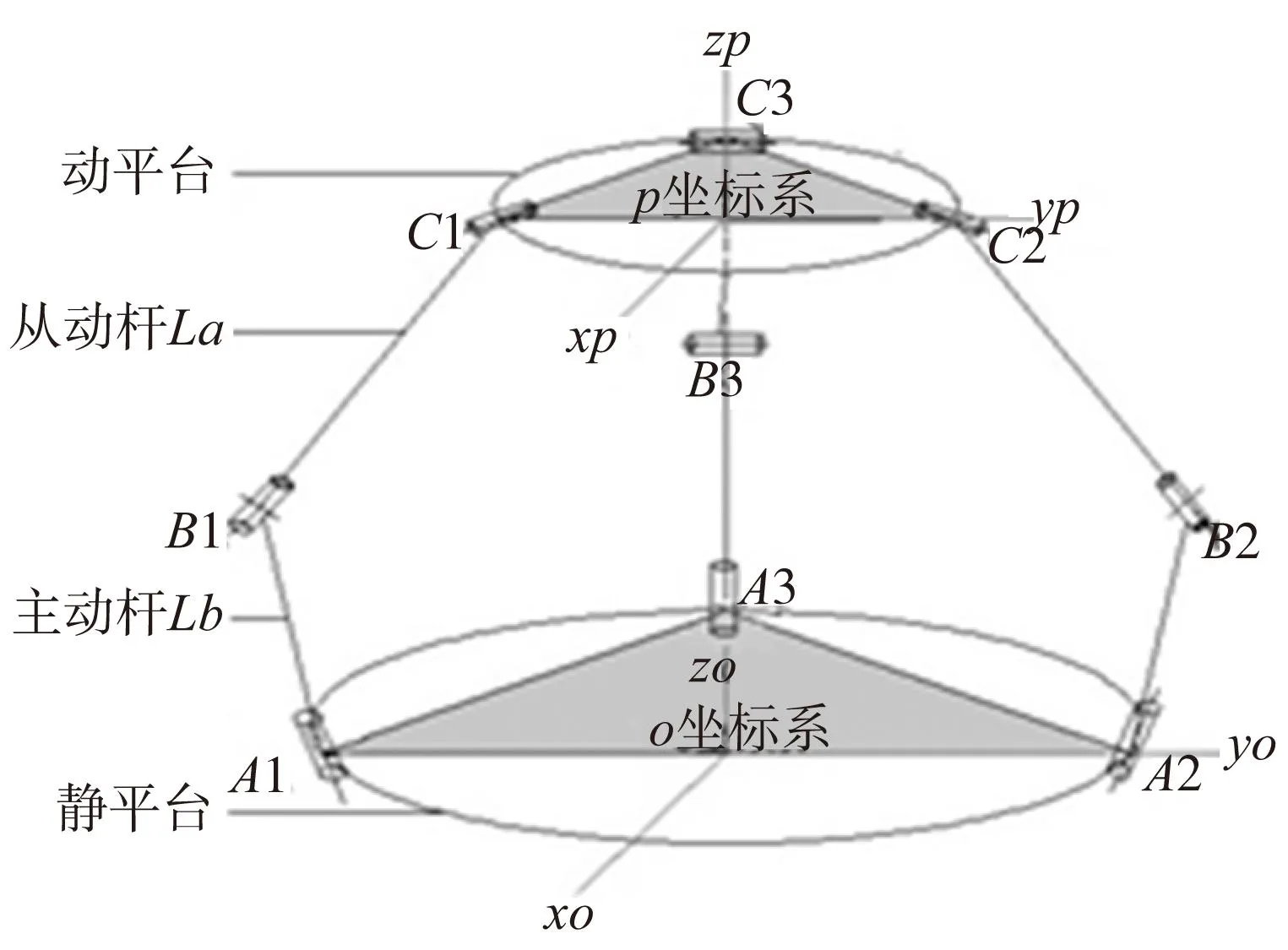
图2 并联机构结构简图
Ai—静平台中对应的三个铰点;
Bi—主、从动杆连接的铰点;
Ci—动平台中对应的三个铰点;
ai=π/6+2π(i-1)/3—动、静平台铰点与各自坐标系的夹角;
θi—主动杆绕X轴的转角。
Lai—从动杆;
Lai—主动杆;
其中(i=1,2,3)为三个对称结构的序号。
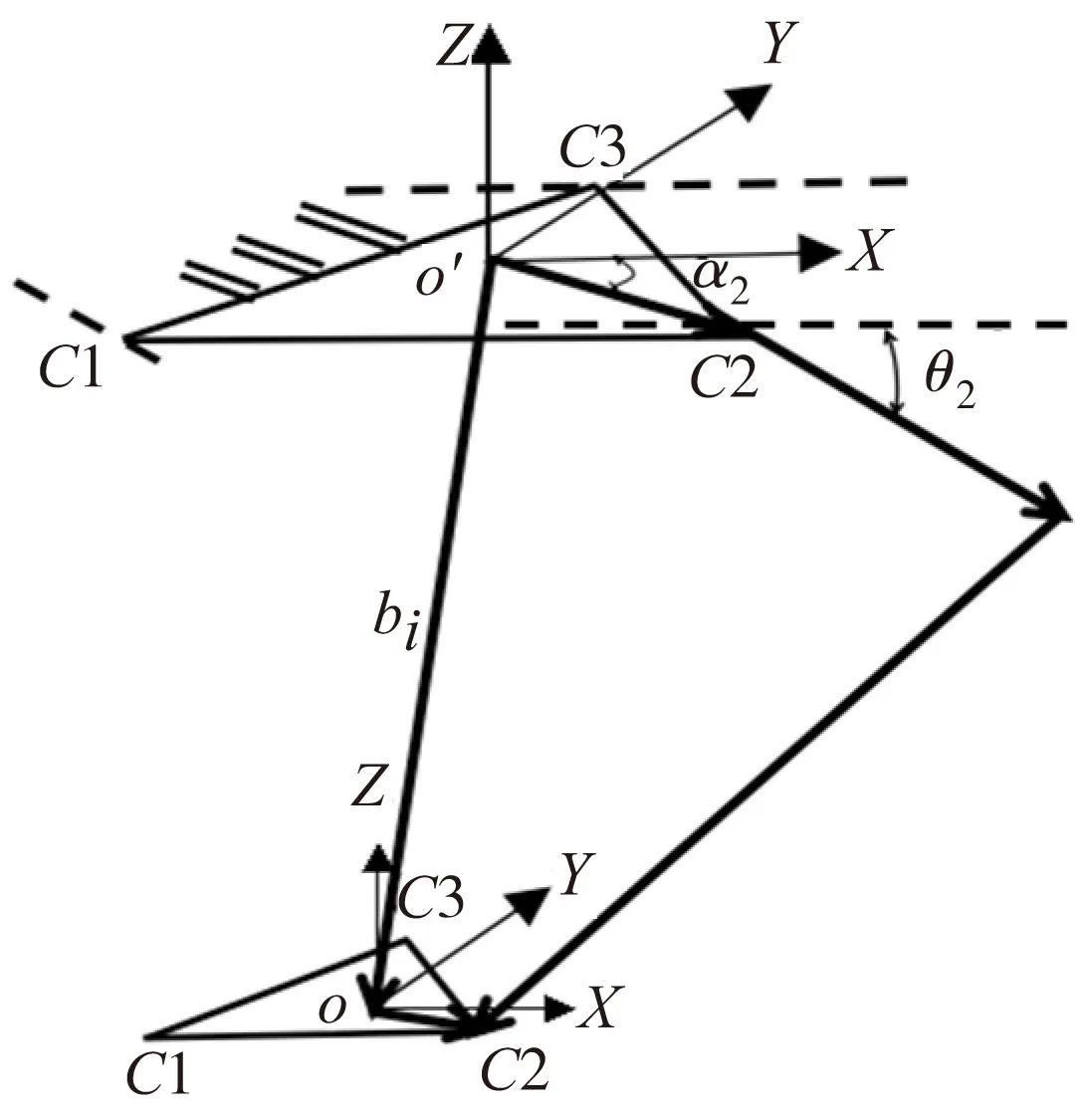
图3 并联机构标定简图
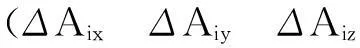
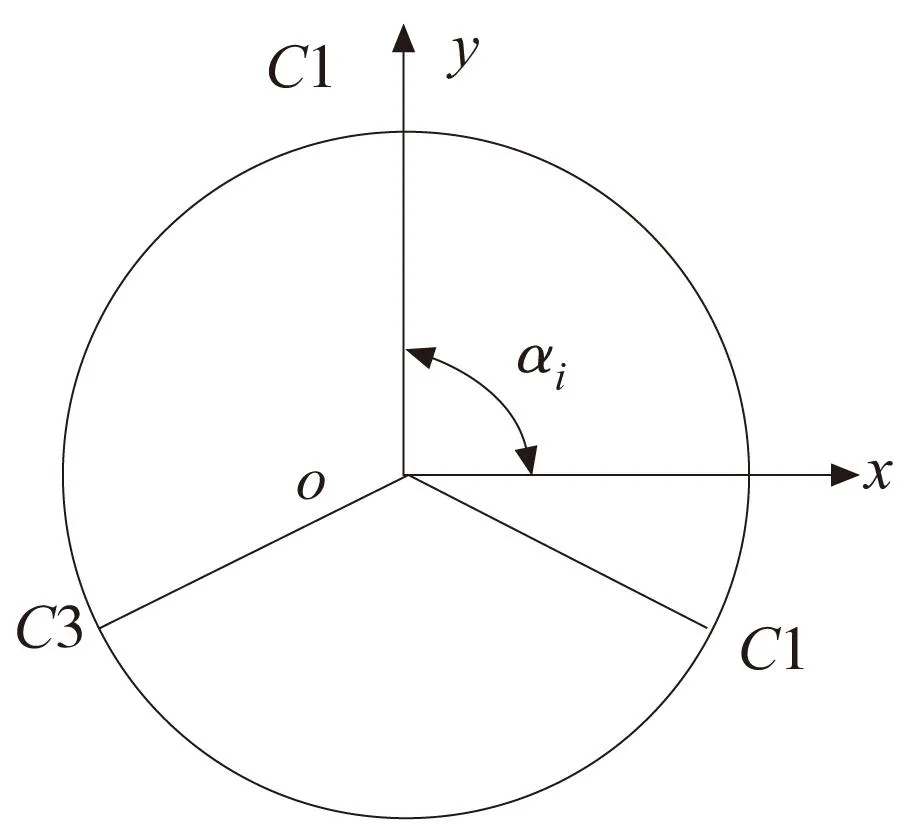
图4 动平台铰点分布
如图4所示,为求解ΔCix、ΔCiy,只需将其转化为求解每个铰点对应的圆半径补偿量Δr和夹角补偿量即可。综上所述,本位最终需要标定的参量为18个,分别是ΔAix、ΔAiy、ΔCix、ΔCiy、Δθi、ΔLai。
2.2标定模型的求解
由文献[8]可得,3自由度并联机构的正解公式为:
(5)
(6)
其中,(xp,yp,zp)为图3中动平台中心点在静平台中的位置坐标;R、r分别为静、动平台中心点到各自铰点的半径值。将公式(5)、(6)整理可得:
Fi(X,θi,αi,R,r,La,Lb)=0
(7)
(8)
将公式(8)化简:
dX=-ABdθi-ACdαi-ADdR-AEdr-AFdLa-AGdLb
(9)
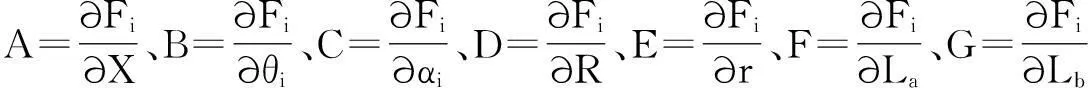
由公式(9)得,
(10)
需要注意的是,此时的补偿模型式(10)中的、和是为了补偿ΔAix、ΔAiy、ΔCix、ΔCiy;其中,
(11)
C、D、E、F、G的形式均与B相似。所以只要能够测取6个以上的位置点,即能够求得所有的补偿值。
2.3测量及计算方案
选取测点:首先保证误差雅可比矩阵非奇异,其次保证机器人历经所有可控的自由度。遥操作的运动空间近似半球形,常用的选点方式是以Z轴为圆心,进行绘制一系列相互平行的圆,共50个,再在这50个圆上由内向外绘制10个平行圆,每个圆上相隔30度取一个位置点,共计(50×50×10)。这种方式取点相对较为繁琐,为更简洁的表现说明问题,采用如图5所示的取点方式,在整体运动空间的对角线上进行选取。
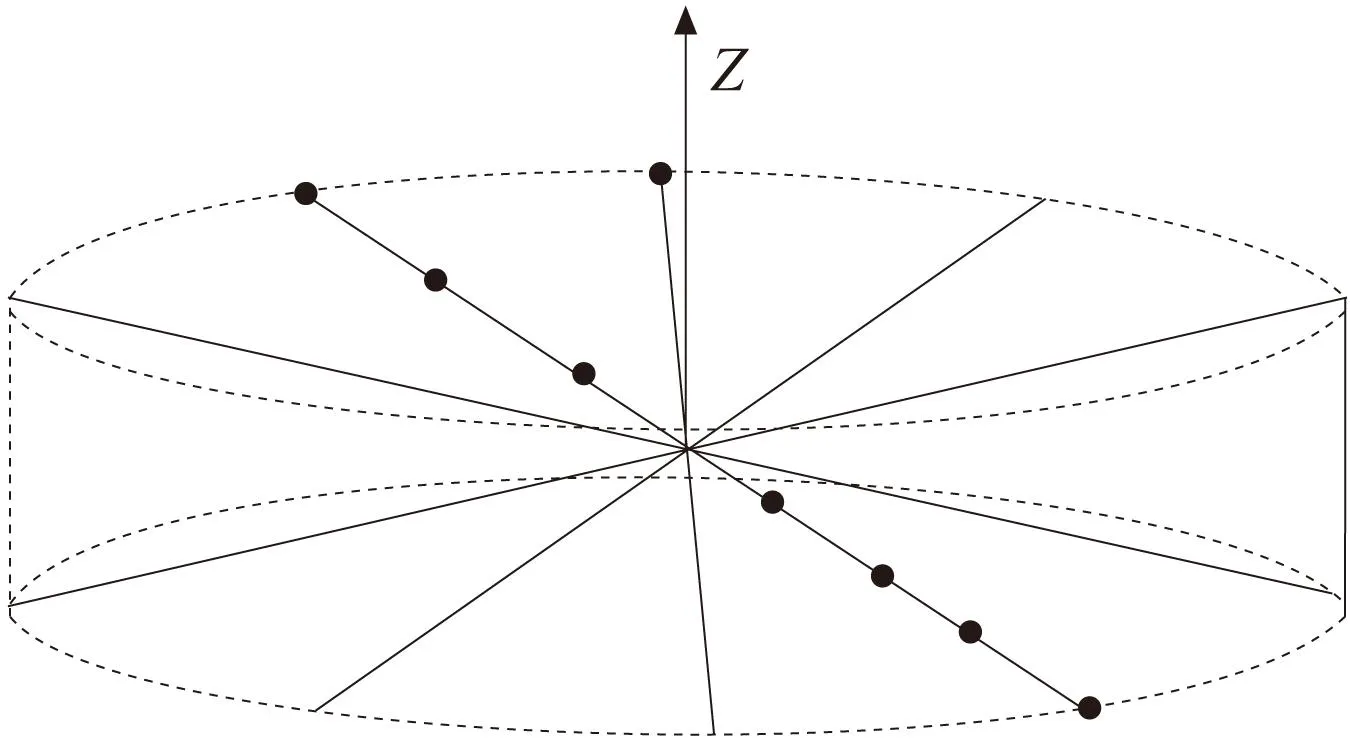
图5 取点示意图
在实际进行标定的过程中,通过激光检测仪测量出末端执行部件到静平台中心点的长度L’以及其单位矢量(cosχsinα,cosχcosα,sinχ),其中,χ为Z轴方向上的夹角,为L’在XY平面内的投影线与X轴的夹角,通过计算可求得实测点的位置坐标。运用最小二乘法计算补偿值,更新理论运动学参数。反复迭代,直到理论输出与实际输出之间的差值满足精度为止。
采用如下的流程框图进行分析计算:
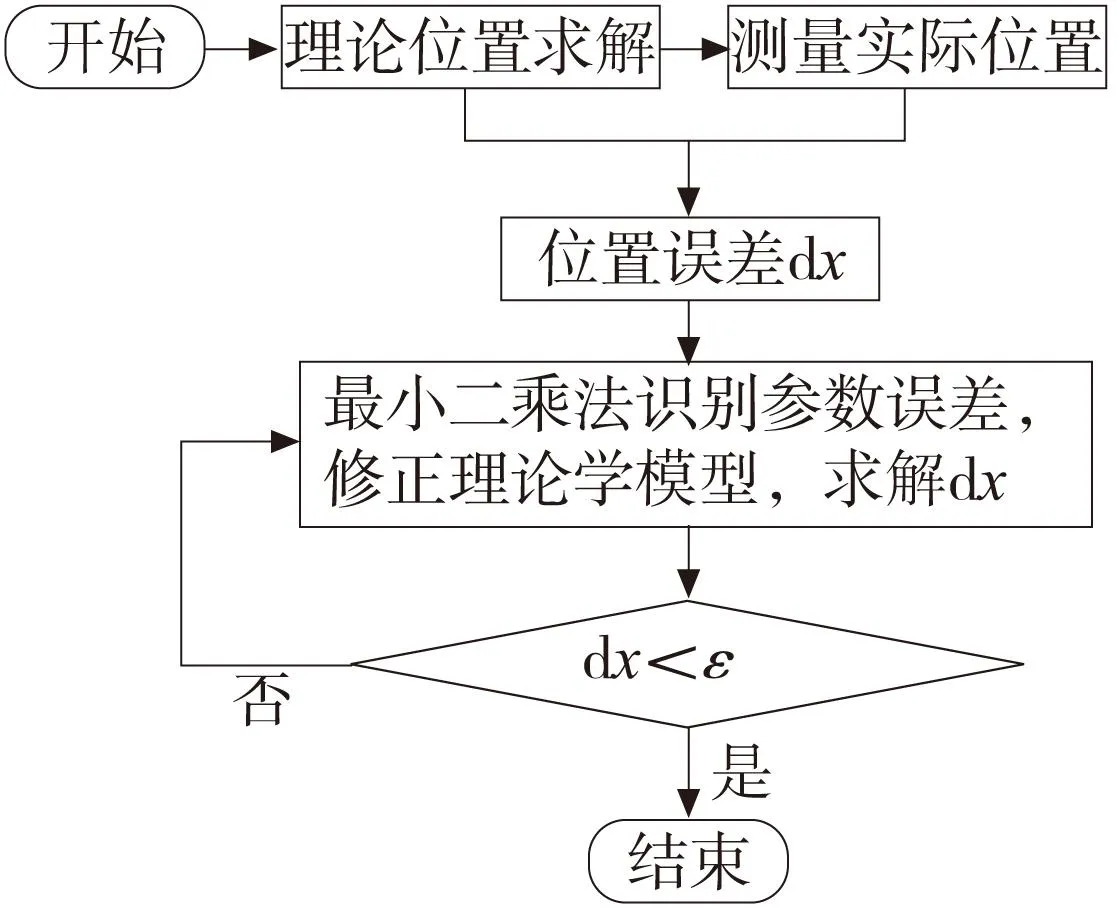
图6 标定流程框图
2.4测量结果分析
由于文章篇幅的限制,下面以选取的20个测量点进行说明。这20个点均是主手机器人在运动过程中能够灵活到达的,不存在边界奇异点的情况。利用前15个点根据上面的流程图计算出补偿值,使用后5个点进行验证所求的结果是否达到预期效果。利用matlab中的最小二乘法构造线性回归方程对参数进行识别。
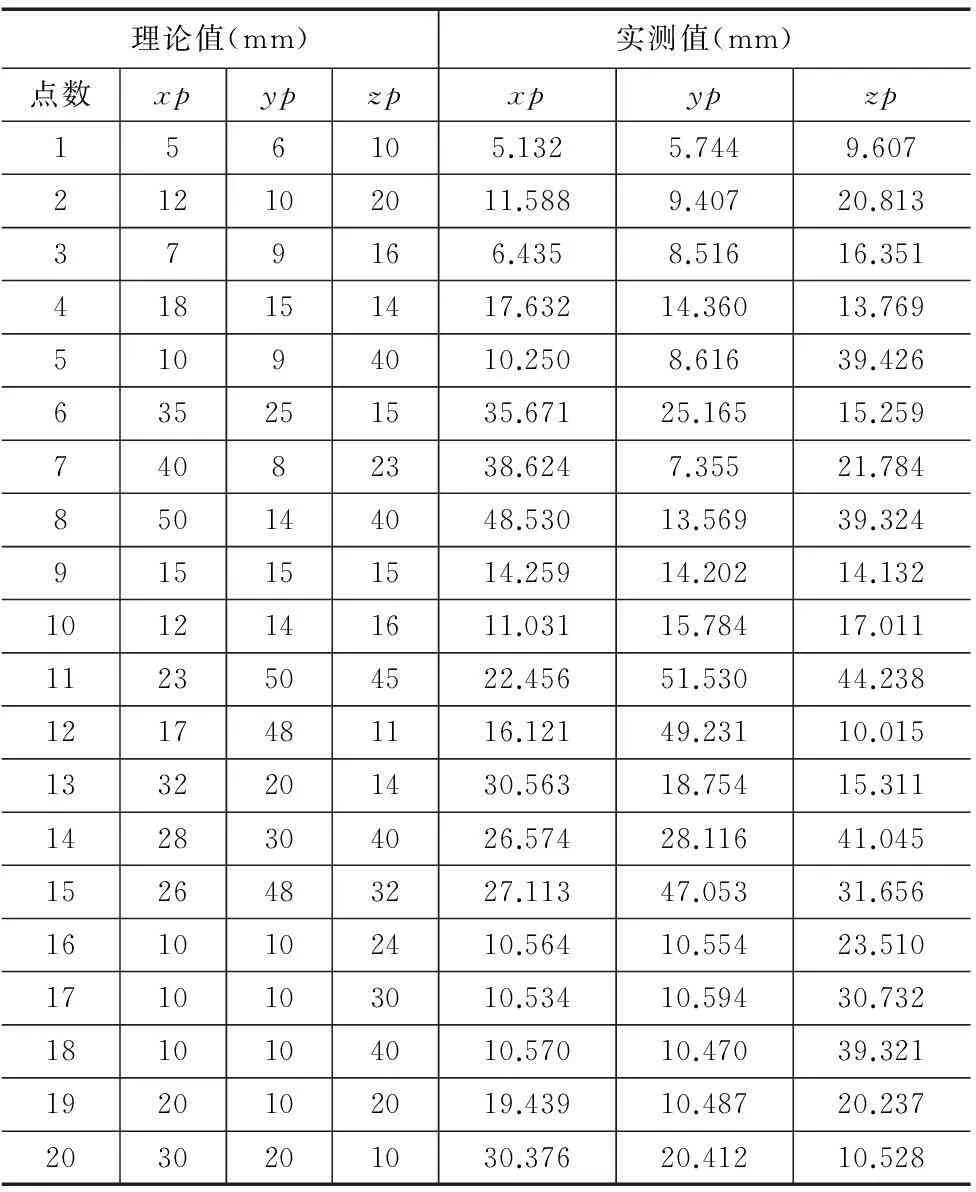
表1 20组实测值与理论值对比
将表1中的数带入公式(10)使用matlab中的最小二乘法[9]对误差进行识别,其18项几何误差辨识结果如表2所示(线性误差项单位:mm,角度误差项单位:deg)
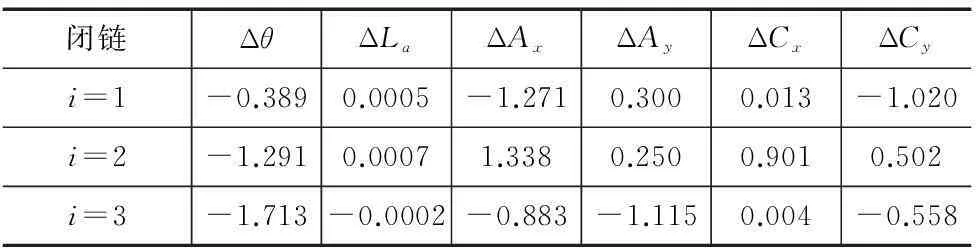
表2 误差辨识结果
3实验结果分析
将辨识的18项误差值带入理论的运动学模型中,求解补偿后的动平台中心点的位置,将补偿前后的位置坐标进行对比,其结果如表3所示。
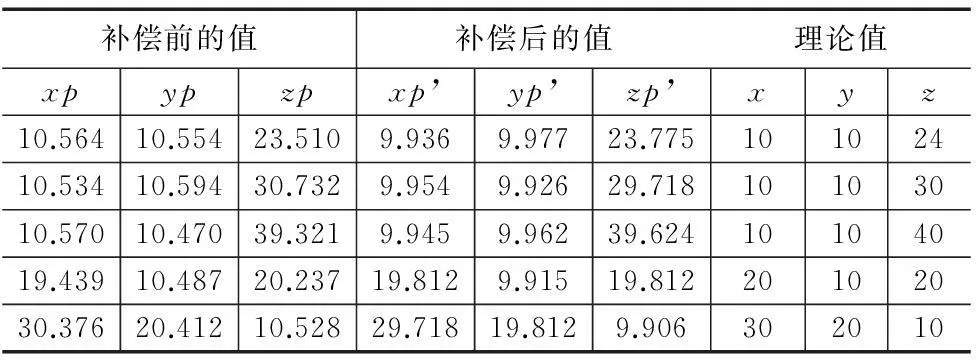
表3 补偿前后机器人的位置在极坐标下的值
定位精度误差常作为机器人运动精度的评定指标,其计算公式为:标定前,标定后:文献[10]的计算结果如表4所示。
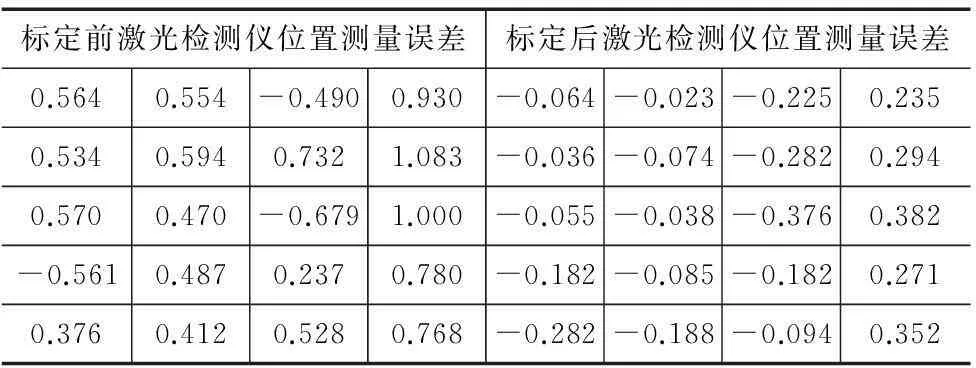
表4 标定前后定位误差
标定前后的定位误差如图7所示。
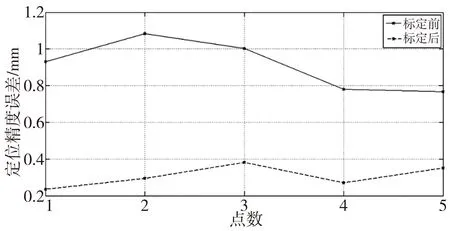
图7 标定前后定位误差
本文用标准方差、均方根误差、最大误差作为对定位精度进行验证[11-12]:
标准误差的求解公式:
(12)
均方根误差的求解公式:
(13)
最大误差的求解公式:
(14)
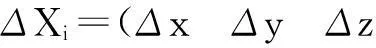
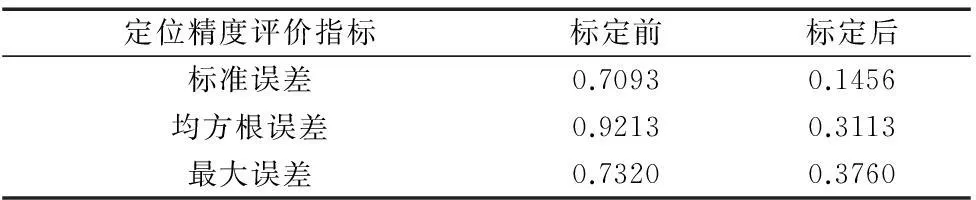
表5 标定结果评价验证
4结论
开发了一款遥操作并联机器人,利用构造的封闭环识别参数误差源,分析排除在求解过程中可避免的误差源,利用机构的运动学正解方程构造了参数误差的雅克比矩阵,结合最小二乘法对其进行误差识别,将标定前后机构的定位误差对比标定后,各几何误差均控制在小范围之内,计算结果符合实际需要,成功的修正了机器人的结合结构参数,从标定前后的定位误差、标准误差、均方根误差、最大误差4个评价指标上,验证了改标定方案改善了机构的绝对定位精度。
标定后机构绝对定位精度有了一定的提高,但此精度还无法满足高精度场合的要求,仍需进一步提高。为此,在进一步的标定过程中①需要设计高精度模具,在初始数据的测量中得到更高的精度。②将连杆的重力因素加以考虑,不仅仅是补偿其拉伸方向的值,对其产生的扭转变形也加以补偿。③改进测量的方法,使得测量的实际数据更接近与真实值,更有效的识别出参数误差。
[参考文献]
[1] 张国庆,杜建军.精密小型Hexapod并联机器人标定实验及精度分析[J].纳米技术与精密工程,2013,11(1):34-40.
[2] Zhuang H Q, Roth Z S. Method for kinematic calibration of Stewart platforms[J].Journal of Robotic Systems, 1993, 10(3):391-340.
[3] Masory O, Wang J, Zhuang H Q. On the accuracy of a Stewart platform-Part II Kinematic compensation and calibration [C]// Proceedings of IEEE International Conference on Robotics and Automation. Atlanta GA, USA, 1993,1:725-731.
[4] 刘新山,周宝庆,王冠群,等.一种双摆工作台式五轴联动机床动态精度的标定方法[J].组合机床与自动化加工技术,2013(5):19-22.
[5] Jdd R P, Knasinski A B.Technique to calibrate industrial Robots with experimental verification.IEEE Trans.on Robotics&Automation,1990,6:20-30.
[6] Mooring B W, Padavala S S Effect of kinematic model complexity on manipulator accuracy In:Proceedings of IEEE Inter.Conf.on Robotics and Automation,1989:593-598.
[7] 彭彬彬,高峰.并联机器人的标定建模[J].机械工程学报,2005,41(8):132-135.
[8] 李长军.面向外科手术的力反馈型遥操作主手研究[J].哈尔滨:哈尔滨工业大学,2010.
[9] 唐国宝,黄田.Delta并联机构精度标定方法研究[J].机械工程学报,2003, 39(8):55-60.
[10] Jiangping Mei, Yi Li, Ce Zhang.The error modeling and accuracy synthesis of a 3-DOF parallel robot delta-s[D].Proceedings of the 9 th Biennial ASME Conference on Engineering Systems Design and Analysis,2008.
[11] 杨丽红,秦绪祥,蔡锦达,等.工业机器人定位精度标定技术的研究[J].控制工程,2013,20(4):785-788.
[12] 吴彬彬,黄筱调,方成刚,等.数控成形磨齿机在线测量系统标定误差的辨识及补偿[J].组合机床与自动化加工技术,2015(6):74-77.
(编辑赵蓉)
Research on Teleoperation Master Hand Robot with Precision Calibration
LUO Ji-man, LI Gen-biao
(School of Mechanical Engineering,Shenyang Jianzhu University, Shenyang 110168,China)
Abstract:In this paper, proposing the method of use laser detector and least squares calibration for parallel robot in order to improve the accuracy of the Master hand parallel robot.By process of kinematic closed-loop chain to identify valid parameter error sources, The use of the robot kinematics Positive Solutions construct Jacobian errors matrix equation .The method is,Firstly, through laser detector to measure actual position of the end part in robot movement ,then,using the least squares method for solving constructed error Jacobian matrix and identify error parameters,the error compensation to theoretical pharmacokinetic model and solve contains the location of the end of the execution unit errors,comparing before and after values of the calibration to theoretical values .Finally, though precision and standard deviation or root mean square error and other performance evaluation to test calibration results.The results show that the positioning accuracy after calibration by 65% than before and standard error than the previous increase of 79.47%, absolute positioning accuracy and stability of the institutions is improved.
Key words:teleoperation master hand robot ;laser detector;least squares;calibration
中图分类号:TH165;TG659
文献标识码:A
作者简介:罗继曼(1966—),女,四川双流县人,沈阳建筑大学教授,研究方向为机器人设计和制造技术,(E-mail)Syljm2006@sjzu.edu.cn。
*基金项目:国家科技计划课题—精细遥操作主从机器人与人机交互控制系统(2012GB102005)
收稿日期:2015-07-15;修回日期:2015-08-11
文章编号:1001-2265(2015)12-0019-04
DOI:10.13462/j.cnki.mmtamt.2015.12.006
