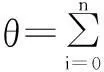基于离心角变化的椭圆插补算法研究*

李银华，赵　凡，黄军垒

(1.郑州轻工业学院 电气信息工程学院，郑州　450002；2.郑州斯倍思机电有限公司，郑州　450001)



基于离心角变化的椭圆插补算法研究*

李银华1，赵凡1，黄军垒2

(1.郑州轻工业学院 电气信息工程学院，郑州450002；2.郑州斯倍思机电有限公司，郑州450001)

摘要：为提高椭圆焊缝的焊接质量，针对现有插补算法存在的不足，研究一种基于椭圆离心角变化的插补算法。该算法通过离心角增量来计算插补点横纵坐标进给量与相应进给速度，并将其传给相应伺服电机。在焊接中算法可时刻保持椭圆焊缝焊接线速度一致，焊缝平滑，确保焊接质量。分析算法的基本原理，算法实现步骤并进行仿真实验。仿真结果进一步验证算法的可行性、有效性与优越性，为椭圆焊缝的实现提供了一种新的理论依据。

关键词：离心角；椭圆；插补算法

0引言

据统计表明，90%散热器漏水漏气现象都是由焊接质量不好所造成的[1]。目前大多数厂家对于复杂焊缝焊接是采用手工焊接。手工焊接对工人的技术要求高，由于氩弧焊的危险性，工人不能长期从事此行业，以免危害身体，这就造成了行业内熟练工人的短缺。有部分厂家采用自动焊，其焊接系统是由雕刻机改装而成，由于焊机本身磁场较大，会对焊接系统产生很大干扰，极大地影响了焊机焊接轨迹，使得焊机不能严格按照所给焊道进行焊接，严重影响焊件质量。因此如何才能高效地实现高质量焊接就成为亟待解决的问题。本文主要研究的是椭圆焊缝自动焊接，主控制器采用软PLC，研究的重点是椭圆焊缝的插补算法，使其可保证焊接平滑性与焊接高质量。

自动化系统常用插补算法有逐点比较法与数字积分法(DDA)。逐点比较法可以保证在焊接过程中速度的平和性，但在多轴联动系统中插补不均匀，这对于对密封性能要求较高的散热器管道焊接来说，很不适用；数字积分法利用弦长近似等于弧长来求插补点，在多轴联动系统中易于实现，且运算效率高，很适用于函数运算。但其在计算过程中使用了除法，使得数据处理起来比较复杂，且在实现过程中速度会随着被积函数的大小而变化，插补速度不平稳，插补精度不高，很容易产生焊接缺陷[2-4]。文献[3]提出了一种比较积分法，结合了比较法和积分法的优点，在每一次脉冲进给时需比较各坐标进给脉冲间隔的大小，才能确定每次具体进给的基准轴，每输出一个脉冲就得作偏差判别、坐标进给和新偏差计算，此外还需要进行过象限处理，计算繁琐[5]。本文基于生产实际情况考虑，提出了一种基于椭圆离心角变化的插补算法，该算法基于软件可很大程度上发挥上位机的计算优势，加快系统运行速度，减小硬件部分的负担。

1焊接要求

散热器焊接，包括管板焊接与管管焊接，本文主要研究管板焊接。管板焊接通用的几种方法：手工氩弧焊、焊条电弧焊、脉冲自动全位置氩弧焊[6-7]。脉冲自动氩弧焊是管板焊接的主流发展方向。在焊接过程中焊接线速度基本一致，不会出现因材料受热不均匀所产生的焊不穿或焊透等缺陷，使得焊接质量、加工柔性、焊接精度等都显著提高，这是自动化焊接的基本要求。

散热器的管板焊接轨迹为几个并排的椭圆，如图1所示。

图1　散热器焊接图

焊机控制的核心问题就是如何控制焊枪的移动，如何使焊枪能够按照指定轨迹运行。在管板类型焊件的实际焊接过程中，由于焊件受热会变形，导致焊缝收缩，焊接轨迹会发生变化，因此要实时修改焊接的轨迹，是非常必要的。而且在焊接过程中，焊接不可能严格的按照预定的焊接轨迹来运行，即使预定轨迹是直线，也不可能。因此，要实时的提供无限的接近圆弧的直线来实现椭圆轨迹的焊接，这就需要研究适合椭圆曲线的插补算法[8]。

2插补算法的选择

在焊接系统中运用比较普遍的可控步长实时插补算法，它适用于相交的圆柱管相贯线接缝的焊接[8]。这种曲线线速度与角速度之间有明确的函数关系，计算比较简单，而椭圆曲线角速度与线速度的函数关系比较复杂，用类似的算法很难得出进给量。

文献[9]采用基于弧长的插补算法，直接利用弧长来求插补点，根据x与y两个变量对弧长的影响程度将椭圆曲线分成了四个区域，然后各自求其弧长、插补点与进给量[9]。这种方法精准度很高，但是计算过于复杂。

为选择一种适用于椭圆圆弧的插补算法，要以实现快速、简便、并能达到一定精度要求为主要目标[10]。运用可控步长实时插补算法的设计理念——根据角度的变化推导出各个坐标轴的进给量，加以改进，简化其计算过程，根据椭圆的参数方程，推导出变离心角实时插补算法。此种算法不需考虑插补过程中的步长问题，插补全过程都保持线速度一致。插补过程中根据具体的运动轨迹确定焊接曲线的变化，并转化为离心角的变化，由此来推导具体插补轨迹。

3变离心角插补算法

对椭圆曲线焊接是通过微小直线段来无限逼近的，因此插补算法需解决的重点就是对直线段的轨迹和速度的确定。

本文所研究的变离心角插补算法，就是在线速度与插补步长一定的情况下，根据椭圆曲线及步长值得到下一插补点的离心角增量，已知起始点坐标和离心角的增量，就可以根据椭圆的参数方程计算出下一插补点的坐标值，进而可以推导出下一插补点各坐标的进给量与进给速度，以此类推就可得到有限步插补的进给量与进给速度。将各坐标轴的进给量与速度作为控制量来控制相应轴的伺服电机，即可实现椭圆曲线的焊接。最终的插补效果就是用有限条等长的直线段去无限接近椭圆上的圆弧。前提是每次插补的线段长度是一定的。由于椭圆曲线的曲率不断变化，使得等长的直线段对应的圆弧长度和离心角的大小都不相同，所以称为变离心角插补算法。计算过程使用椭圆的参数方程所求得变化后的坐标值，因此在插补过程中不会产生累计误差，插补精度较高。

3.1算法原理

在已知椭圆中，设其长轴为a，短轴为b，则椭圆的参数方程为：

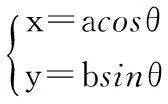
(1)

式(1)中的θ与圆的参数方程中的φ意义不同，圆的参数方程为：

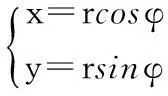
(2)

其中r为圆半径，参数φ是圆半径的旋转角，称为圆心角。θ是椭圆长轴(或短轴)所对应曲率圆半径的旋转角，如图2所示，称为椭圆离心角，如图中∠AOD为点C的离心角。设椭圆上任意点为M(xi,yi)、N(xi+1,yi+1)，则M、N点对应离心角为θi、θi+1。椭圆中也有圆心角之说，椭圆圆心角ψ是指椭圆上的点与椭圆焦点O之间的连线与X轴所形成的角，如∠COD为点C的圆心角。椭圆的离心角θ和圆心角ψ之间的关系为：

(3)

图2　椭圆离心角示意图

椭圆上点M到焦点O距离OM为点M对应的曲率圆半径Ri，则OM=Ri，且有

(4)

插补步长ΔL与插补周期T、线速度v三者满足关系式：

ΔL=v×T

(5)

若T一定，系统确定了v，则插补步长ΔL亦可确定。而v是X轴方向速度vx与Y轴方向速度vy合成值，三个量之间满足三角函数关系[11]：

(6)

在实际运行中，焊接的起始点确定，坐标为(xi,yi)，则起始的离心角θ与圆心角ψ也确定。在焊接过程中，随着插补轨迹从M点移动到N点，离心角由θi变为θi+1，离心角增量Δθ可表示为：

(7)

如果焊接时采用顺时针方式进行焊接，则圆心角ψ和离心角θ会越来越小。反之，采用逆时针，圆心角ψ和离心角θ会越来越大。

在具体插补中，若插补周期T很小，且ΔL<

(8)

因此，知道第i个插补点M的坐标(xi,yi)，便可根据式(7)与式(8)得出第i+1个插补点N的离心角θi+1。从M点到N点的横纵坐标的增量Δxi+1、Δyi+1的求解公式为：

(9)

根据式(9)和式(1)，由椭圆第i个插补点的坐标(xi,yi)即可得出第i+1个插补点N的坐标(xi+1,yi+1)及相应坐标轴进给量Δxi+1、Δyi+1。各轴的进给量与进给速度满足关系式为：

(10)

由此推算出各轴的进给速度。插补过程实质就是控制伺服电机的速度和进给量，使其能够按照给定的速度和位移来进行移动，用有限条无限接近圆弧的直线段代替圆弧，实现椭圆轨迹的焊接。这种插补方法是由椭圆离心角变化推导出插补进给量和插补速度，因此称为变离心角增量插补方法。

3.2插补步骤

焊接轨迹由两排相同大小的椭圆焊孔组成。在实际焊接中，若先沿一排焊孔焊接会造成工件严重变形，因此，需要在保证焊接完整的基础上，在上下两排焊孔之间来回焊接。对于具体椭圆的焊接，我们只需要研究其中一个椭圆的插补算法即可。

在实际焊接过程中，如果线速度不一致，就会造成焊接轨迹不均匀，严重者会造成焊不透或焊穿。因此在焊接过程中要始终保持焊接速度一致性，即线速度v不变。

在插补过程中，插补步长ΔL和插补周期T是固定的，由式(5)可知线速度v也确定，保证了焊接过程的实际需要。

具体插补过程流程图如图3所示。在椭圆参数方程中，都是以椭圆焦点作为原点，在实际插补过程中往往不能满足这个条件，因此在插补开始前需进行坐标转换。

图3　插补过程流程图

3.3插补实例

在焊接控制系统中，插补算法将得到横纵坐标进给量和进给速度传递给相应的伺服电机，使伺服电机带动焊枪按指定轨迹移动，如图4所示。

图4　插补示意图

为验证此算法的插补效果，需在软件上进行算法仿真。

设椭圆其长轴a=20mm，短轴b=16mm，起始点坐标为(0,16)，仿真过程只插补第一象限，则终点坐标为(20,0)，采用顺时针方式，插补速度为5mm/s，插补周期为10ms，则插补步长值为0.05mm，采用变离心角增量插补算法插补此椭圆。根据本文所研究的插补算法公式，得到如图5a的实际插补轨迹图。由于在实际操作中，焊缝是由一个个焊接点组成，因此在仿真过程中，采用圆点来代替焊接点。图5b是理想椭圆曲线与焊接曲线的对比图。由两种轨迹对比，可知插补算法达到了预期的目的，可实现焊接。插补的结果很平滑，插补曲线即为给定的焊接曲线。由于插补算法是建立在椭圆曲线的参数方程的基础之上，每个插补点都满足此方程。因此插补的步长值的选择将直接影响到焊接的精度。在实际运行过程中，要根据实际焊机运行情况选择适合的焊机速度与插补周期，以期得到最好的焊接轨迹。

图5　仿真图

图6　插补轨迹路线图

图6是各种不同插补算法的具体插补轨迹，逐点比较法每一步只能提供某一个方向的插补进给，并由偏差方程确定下一个插补点的具体方向，只需要满足向使加工偏差减小并趋向轨迹终点的方向插补即可，插补效果如图6a所示。因此插补的精度比较低，不适用于对插补精度要求高的场合[13]。

比较积分插补算法是根据偏差函数来判断进给方向并确定进给量，插补点不一定都在椭圆曲线上，因此插补的误差比较大，会造成焊接的轨迹偏离原轨迹，如图6b所示，影响焊接的美观性和焊接质量[14]。

运用变离心角插补算法所得出的每个插补点都满足椭圆方程，因此插补点不会产生偏差，如图6c，插补的结果相对的比较贴合椭圆轨迹，提高了插补的精度和质量。不同的算法其逼近方法不同，就造成了插补精度的差异，影响焊接质量。

这种变离心角增量插补算法其优点如下：

(1)每一个插补点的坐标都是满足椭圆方程，因此都在椭圆曲线上，不会因为插补次数太多而产生累积误差，但会因为计算精度问题而产生逼近误差，这是不可避免的。

(2)运用原理和计算方法简单，每次插补时，同时给出两个坐标轴的进给量，且不用考虑跨象限问题，实现方便。

(3)插补过程速度平稳，满足曲率大的地方步长值小，使焊机焊接均匀，质量稳定。

该算法的不足之处是：插补过程中，所用点的坐标都是基于椭圆焦点为圆心时所计算的结果，因此在每个椭圆插补之前，都需要进行坐标转换，这增加了程序编写的难度和复杂度。

4总结

本文通过分析了以往焊接插补算法的弊端，将变步长插补算法加以改进，使其适用于椭圆曲线，提出了一种适用于椭圆焊缝的变离心角插补算法，并对算法加以仿真研究，结果表明，此算法插补精度高，很容易实现椭圆曲线焊缝的焊接，对于椭圆焊缝的管板焊接水平的提高有很大的促进所用，可明显提高焊接的质量。该算法可适用于由PLC作为主控制器，由伺服系统作为执行机构的焊接控制系统，伺服系统执行插补算法，实现对各个轴的进给，完成了焊枪的移动，实现对椭圆焊接曲线的焊接。

[参考文献]

[1] 王振民，张栋，李晋,等．基于ARM的全数字管板自动化焊机[J]．焊接学报，2010，31(12)：1-4．

[2] 白刚．基于DSP处理器的DDA插补算法改进措施研究[J]．机电产品开发与创新，2012，25(3)：156-157．

[3] 王琨琦，王润孝，孙林丽．椭圆曲线的比较积分插补方法研究[J] ．西安工业学院学报，2005，25(1)：1-2．

[4] 田浩．椭圆插补的数字积分法研究[J] ．价值工程，2013(17)：33-34．

[5] 陈天炎．一种实用高效的轨迹插补方法——比较积分法[J]．闽江学院学报，2010，31(5)：40-43．

[6] J Kruger, S K Marya． On Recent Trends in Orbital TIG Welding of Tubes[J]．International Journal for the Joining of Materials．1994，6(1)：27-32．

[7] 刘永平．全位置深孔管板焊机机构设计及运动仿真[D].哈尔滨：哈尔滨工业大学，2006．

[8] 霍孟友，王新刚，尹萍．自动焊接相贯线接缝的实时插补控制算法与仿真[J] ．焊接学报，2006,27(11)：37-40．

[9] 殷晨晨，吴文江．基于弧长的椭圆插补新算法[J] ．组合机床与自动化加工技术，2012(4)：1-4．

[10] 龙春国，史耀耀．基于OpenGL五轴联动数控机床仿真的插补算法及软件实现方法研究[J] ．机械科学与技术，2003，22(11)：183-185．

[11] 杨帆，廖知，肖贝,等．改进插补算法在数控雕刻系统中的应用[J]．华中科技大学学报，2011，39(2)：27-31．

[12] 朱国力，段正澄，黄胜,等．基于圆心角分割的椭圆插补算法研究[J]．机械工业自动化，1996，18(1)：41-43．

[13] GAN Ming，LIN Gui-qing，YUAN Zheng-ping． Elliptic Interpolation of Multi-Arc Fitting and Adaptive Algorithm[C]．2009 International Conference on Environmental Science and Information Application Technology,608-610．

[14] 赵庆志，席港港．基于基础坐标概念的逐点比较法圆弧插补原理及其应用[J]．制造业自动化，2012，34(11)：69-71．

(编辑赵蓉)

Research of the Ellipse Interpolation Algorithm Based on Centrifugal Angle Change

LI Yin-hua1,ZHAO Fan1,HUANG Jun-lei2

(1.College of Electric and Information Engineering ,Zhengzhou University of Light Industry,Zhengzhou 450002, China; 2.Zhengzhou Spaceme Co. Ltd., Zhengzhou 450001, China)

Abstract：Improving quality of elliptical welding an ellipse interpolation algorithm based on centrifugal angle change was been proposed against the deficiency of interpolation algorithm in existence. The feed and feed speeds of interpolated points were calculated with the increment value of centrifugal angle to control servo motors in this algorithm. Line velocity can remains constant during welding, so weld seam is smooth to ensure quality. The theory of algorithm and implementation steps are introduced, simulation experiment is done. Application and result of simulation shows that algorithm is feasible, has a high accuracy, calculates simply. Therefore, a new theoretical basis for welding of ellipse is provided.

Key words：centrifugal angle；elliptic；interpolation algorithm

中图分类号：TH123；TG659

文献标识码：A

作者简介：李银华(1964—)，男，湖北应城人，郑州轻工业学院教授，研究生导师，工学硕士，研究方向为嵌入式系统的开发、智能仪表应用及自动化控制系统，(E-mail)zzfcc@126.com。

*基金项目：郑州轻工业学院校研究生科技创新基金第一批立项项目(01002)；2013年河南省重点科技攻关计划项目(132102210057)；2013年郑州市产学研项目(131PCXYY141)；2014年郑州市工业重点攻关项目(141PZDGG119)

收稿日期：2014-12-30；修回日期：2015-03-06

文章编号：1001-2265(2015)12-0039-04

DOI:10.13462/j.cnki.mmtamt.2015.12.011