铣削颤振及其可靠度分析*

冯吉路，孙志礼，孙洪哲，柴小冬

(东北大学 机械工程与自动化学院，沈阳　110819)



铣削颤振及其可靠度分析*

冯吉路，孙志礼，孙洪哲，柴小冬

(东北大学 机械工程与自动化学院，沈阳110819)

摘要：通过铣削颤振动力学建模，考虑了影响参数的随机性，在解析法分析铣削系统阻尼比、刚度、固有频率、铣削径向切削宽度以及铣削力系数对铣削颤振稳定性的影响的基础上，应用蒙特卡洛算法，分别对不同阻尼比和刚度的铣削系统进行了铣削颤振可靠性分析。结果表明，主轴转速和铣削颤振可靠度呈现明显的非线性关系。在稳定域按照极限切削深度进行铣削加工时，仅有在特定速度段能够保障不发生颤振现象，刚度的增加几乎不会影响铣削颤振可靠度，增加铣削系统阻尼可容易地得到铣削稳定域所对应的主轴速度。

关键词：铣削颤振；极限切削深度；可靠性；蒙特卡洛

0引言

铣削加工是一种最常见和最通用的加工方式，其具有良好的材料去除性能，因此在工业生产中扮演了重要的角色[1]。然而，在某些条件下铣削加工过程中会产生颤振现象，这不仅会引起铣削系统的自激振动和受迫振动，从而导致加工过程中的噪声加剧，并且会影响被加工工件的表面质量和刀具的使用寿命，严重的影响加工效率[2]。因此，研究人员对铣削加工过程中的颤振预测和颤振抑制进行了广泛的研究。

Tobias和Tlusty等[3-4]首先提出了切削过程中的颤振稳定性预测模型，建立了单自由度特征方程。Altintas和Budak[5]提出了铣削过程中二自由度的颤振解析模型，该模型建立过程中假设系统的动态参数不变且切削系数是时不变的。迟玉伦等[6]对铣削颤振稳定域叶瓣图确定方法进行了研究，得到了与实验测量结果相一致的铣削颤振稳定域叶瓣图。刘战强等[7]通过分析斜角切削的几何关系，分析了铣刀参数对铣削稳定性的影响。祝长生等[8]应用内置力执行器对铣削颤振进行了主动控制，并在抑制铣削颤振取得了明显效果。李茂月等[9]通过变主轴转速在线抑制颤振算法实现了抑制铣削颤振。Jui-Pin Hung等[10]分析了主轴系统对铣削刀具动态性能的影响，分析得到结构刚度和轴承刚度是影响铣削动态性能的主要因素之一。铣削系统的刚度、阻尼比、固有频率以及材料切削力系数和径向切削深度等值在实际实验测试时，均为随机变量。然而，上述研究并没有考虑铣削系统动力学参数的随机性对铣削颤振的影响，这样会导致即便按照极限切削深度进行加工时，仍然发生颤振现象的情况，因此有必要对铣削系统进行颤振可靠性分析。

本文通过铣削动力学建模仿真，分别分析了各个参数对铣削颤振的影响，得到了铣削颤振稳定性叶瓣图。考虑了铣削系统动力学参数的随机性，通过蒙特卡洛算法对铣削可靠性进行了分析，为实现铣削颤振的主动抑制提供了有效依据。

1铣削颤振动力学建模

在铣削过程中，前一个刀齿切削留下了波纹，由下一个刀齿进行去除，并在新的表面上形成波纹，两个波纹之间的相位移会使得切屑的厚度产生变化，从而使得切削力发生变化。当铣削力变化的频率接近铣削系统的某阶模态时，系统会发生颤振现象。

主轴-铣刀-工件所构成的铣削动态模型如图1所示。铣削系统的刚度和阻尼由主轴-刀具系统决定，模型中铣刀具有4个刀齿，x方向为刀具的进给方向。铣削系统简化模型其动力学微分方程可表示：

(1)

式中，mx、my、ξx、ξy、kx、ky分别为铣削系统X、Y方向上的质量、阻尼和刚度，Fx(t)和Fy(t)分别为刀齿上铣削力在X、Y方向上的分量。

铣削过程中动态铣削力可以表示：

(2)

式中，a为轴向切削深度，Kt为切削系数，[A0]为切削方向系数矩阵，Δ(t)为切削厚度变化。

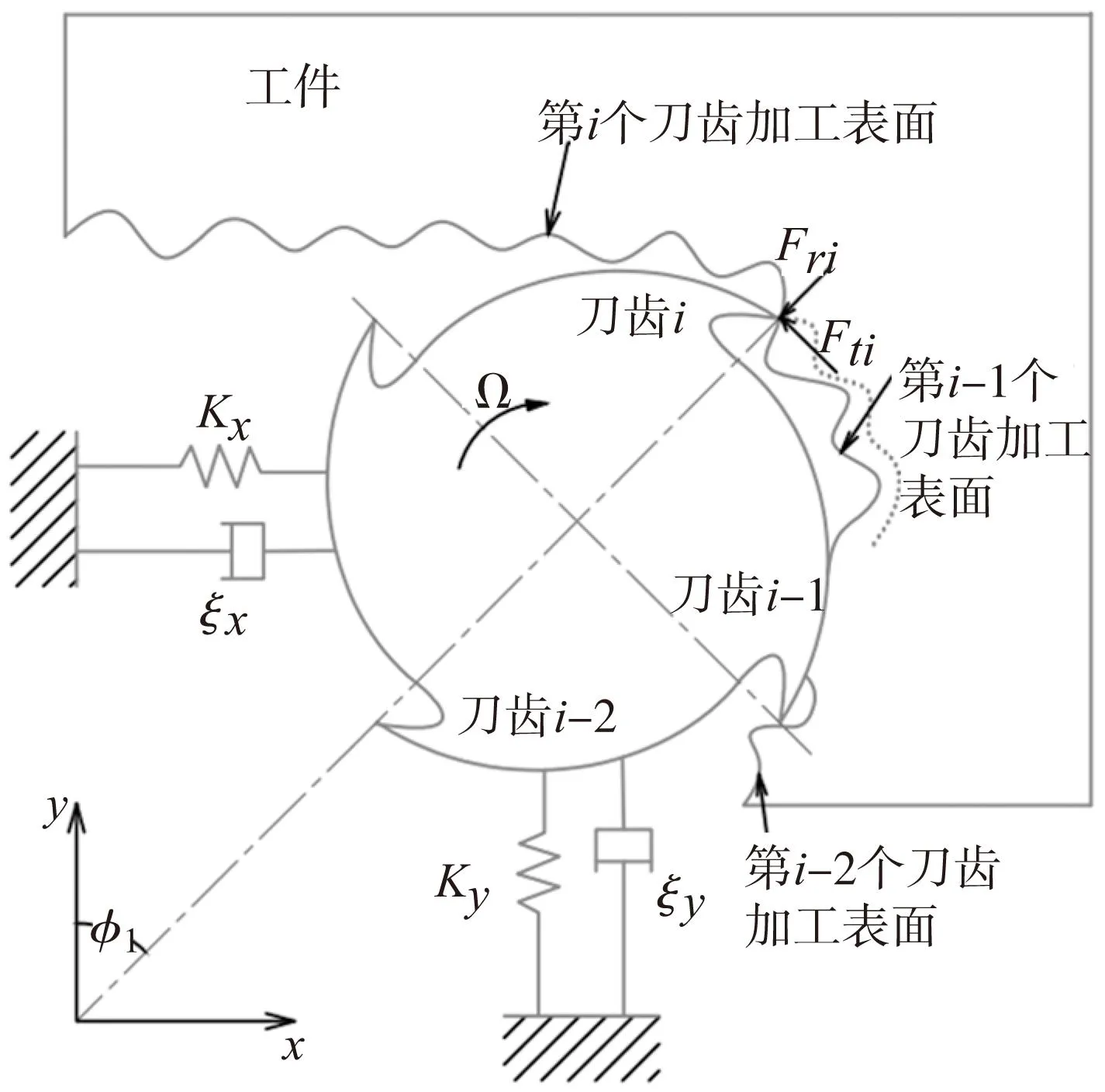
图1　铣削系统动力学模型

考虑再生效应的动态切削力表达式：

(3)

式中，[G(iw)]刀具-工件接触区传递函数矩阵。

通过求解方程的特征根可得到颤振频率为wc时的极限切削深度：

(4)

式中，ΛRe为特征方程的实部，κ为特征方程虚部与实部的比值，N为铣刀的齿数。

根据特征方程虚部与实部的比值可以求得主轴对应的转速：

(5)

式中，k为叶瓣数。

2铣削颤振结果分析

通过对上述方程分析结果可知，铣削颤振稳定性分别由铣削系统的动力学参数、刀具参数和材料属性决定。为分析铣削动力学参数对颤振稳定性的影响，假设铣削系统的X和Y方向的动力学参数完全相同。仿真时的参数分别：Wn=600Hz、ξ=0.02、K=12500N/mm、N=4、Kt=800N/mm2、Kn=170N/mm2、ae=2.0mm。

保持其它影响参数不变的前提下，改变铣削系统阻尼，分析其对颤振稳定性的影响，得到铣削颤振稳定域叶瓣图如图2所示。铣削稳定性叶瓣图随铣削系统阻尼的增加整体上移，极限切削深度随阻尼比的增加而增大。系统阻尼比为0.0125、0.0150、0.0175和0.0200所对应的极限切削深度分别为2.85mm、3.42mm、3.99mm和4.57mm。

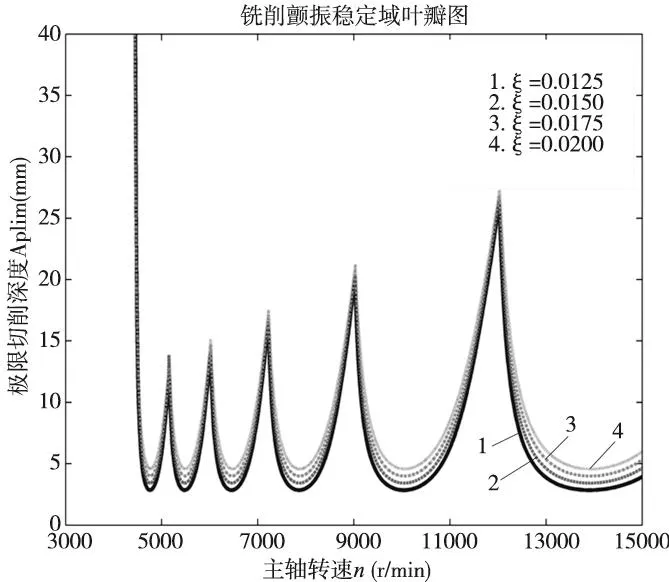
图2　铣削系统阻尼比对颤振稳定性的影响

保持其它影响参数不变的前提下，改变铣削系统刚度，分析其对颤振稳定性的影响，得到铣削颤振稳定域叶瓣图如图3所示。铣削稳定性叶瓣图随铣削系统刚度的增加整体上移，但与图2相比，极限切削深度的峰值变化更为明显。极限铣削深度随系统刚度的增加而增大。铣削系统刚度为12500N/mm、15000N/mm、17500N/mm和20000N/mm所对应的极限切削深度分别为4.57mm、5.48mm、6.40mm和7.31mm。

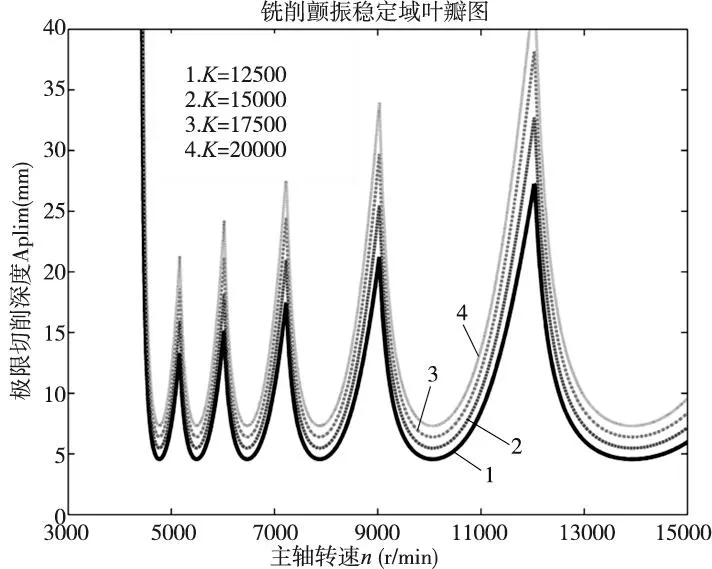
图3　铣削系统刚度对颤振稳定性的影响

改变铣削系统固有频率进行铣削颤振分析，得到铣削颤振稳定域叶瓣图如图4所示。铣削系统的固有频率不会影响极限切削深度，但会使得稳定域叶瓣图整体右移，颤振稳定域的面积逐渐减小。

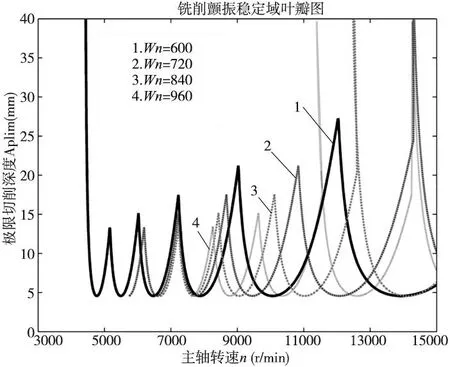
图4　铣削系统固有频率对颤振稳定性的影响

图5为改变径向铣削宽度得到的铣削颤振稳定域叶瓣图。通过分析可得，稳定域叶瓣图会随着径向铣削宽度的增加整体下移。径向铣削宽度的增加会使极限铣削深度减小。即铣削宽度越大，越不容易实现铣削稳定。径向铣削宽度为2.0mm、2.4mm、2.8mm和3.2mm所对应的极限切削深度分别为4.57mm、3.73mm、3.16mm和2.73mm。

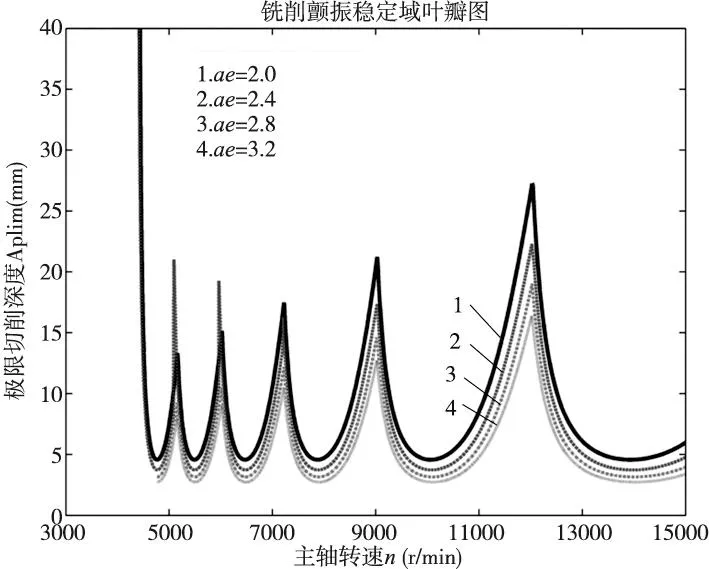
图5　径向铣削宽度对颤振稳定性的影响

如图6所示，铣削力系数变化对颤振稳定性的影响，该图显示极限切削深度与铣削力系数成反比。铣削力系数反应了材料的难加工程度，切削力系数越大，材料越难加工。分析可知，铣削力系数越大，材料加工时越容易产生颤振现象。材料的铣削力系数为600N/mm2、800N/mm2、1000N/mm2和1200N/mm2所对应的极限切削深度分别为6.09mm、4.57mm、3.65mm和3.05mm。

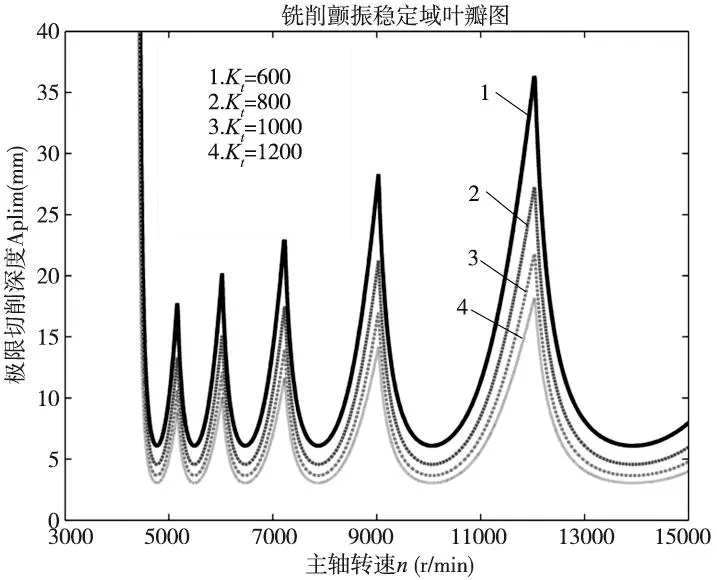
图6　铣削力系数对颤振稳定性的影响

3铣削颤振可靠度分析

在铣削加工过程中，切削深度超过极限切削深度时会发生颤振现象，进而导致被加工工件的表面质量和刀具寿命降低，并会使得切削噪声加剧。在计算得到极限切削深度的情况下，由于机床的动力学参数、材料的铣削力系数和铣削径向切削宽度等参数具有随机性，在使用极限切削深度进行铣削加工时仍然有可能发生颤振现象。

设铣削系统X、Y方向的动力学参数相同，铣削的极限切削深度由下式表达：

flim ap=y(wn,ξ,K,Kt,ae)

(6)

式中，wn，ξ，K，Kt，ae为随机参数向量。假设随机参数服从标准正态分布，其均值为muX=(muwn，muξ，muK，muKt，muae)，根据6σ原则，其方差为sigmaX=0.005muX。

根据铣削颤振定义可得铣削颤振的极限状态函数：

Z=Aplim-flim ap

(7)

当Z≤0时，视为发生铣削颤振现象，当Z>0时，视为正常铣削加工状态。

应用MonteCarlo法对铣削极限状态函数进行n直接抽样计算，其中Z>0的次数为s，因此，铣削颤振可靠度：

(8)

应用MonteCarlo算法进行107抽样模拟，其中，模拟参数muX1=(600Hz，0.02，12500N/mm，800N/mm2，2.0mm)， muX2=(600Hz，0.05，12500N/mm，800N/mm2，2.0mm)； muX3=(600Hz，0.02，12500N/mm，800N/mm2，2.0mm)， muX4=(600Hz，0.05， 25000N/mm，800N/mm2，2.0mm)，方差根据6σ原则进行取值。模拟结果分别如图7～图10所示。

如图7所示，铣削系统阻尼均值muξ=0.02时，不同主轴转速所对应的铣削颤振可靠度。该图中主轴转速和可靠度在低速状态下并没有一一对应的关系。在稳定域按照极限切削深度进行铣削加工时，仅有在特定速度段能够保障不发生颤振现象。在转速为10500r/min～11500r/min时，铣削颤振可靠度等于1，在该条件下铣削工件会获得较好的表面质量。在其它转速下，不能保障不发生颤振现象。

与如图7相对应，图8为铣削系统阻尼均值muξ=0.05时，不同主轴转速所对应的铣削颤振可靠度。该图中主轴转速和可靠度在全转速下存在着一一对应关系，且铣削颤振可靠度在多个转速段等于1。对比图7和图8的结果可得，提高铣削系统的阻尼可以实现对铣削颤振的主动抑制。

通过对比图9和图10可知，铣削系统刚度的变化不会对铣削可靠性产生影响。在转速为5000r/min～8500r/min时，对应的极限切削深度进行铣削加工能够保障不发生颤振现象。

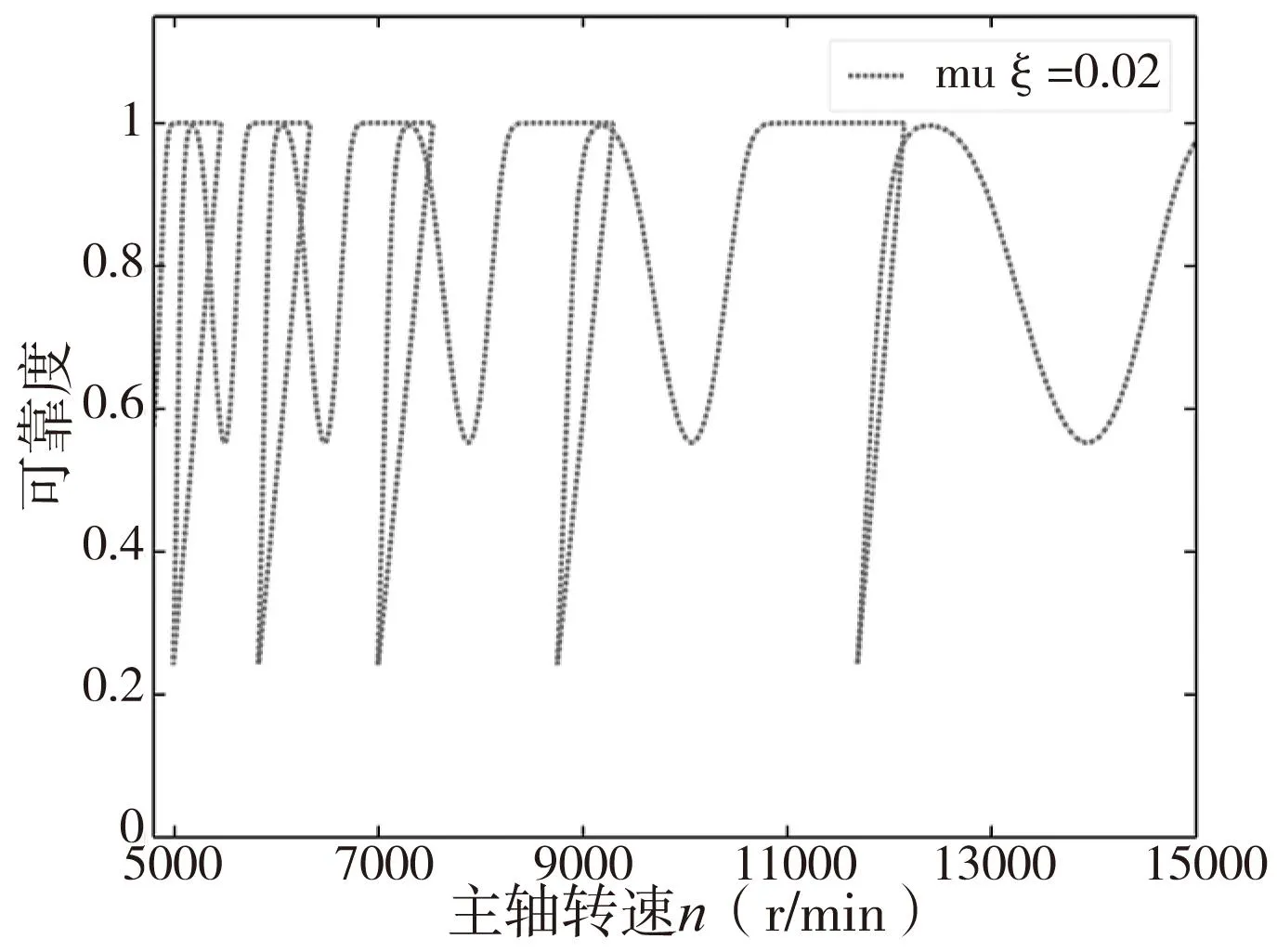
图7　铣削系统阻尼均值muξ=0.02时的铣削可靠性

图8　铣削系统阻尼均值muξ=0.05时的铣削可靠性

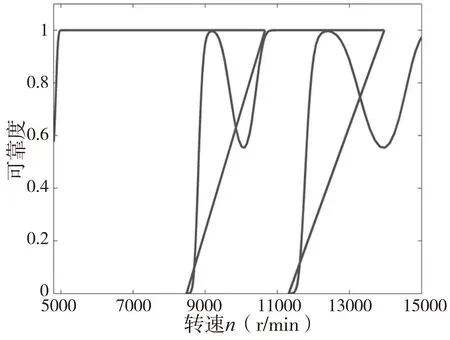
图9　铣削系统刚度均值muK=12500N/mm时的铣削可靠性

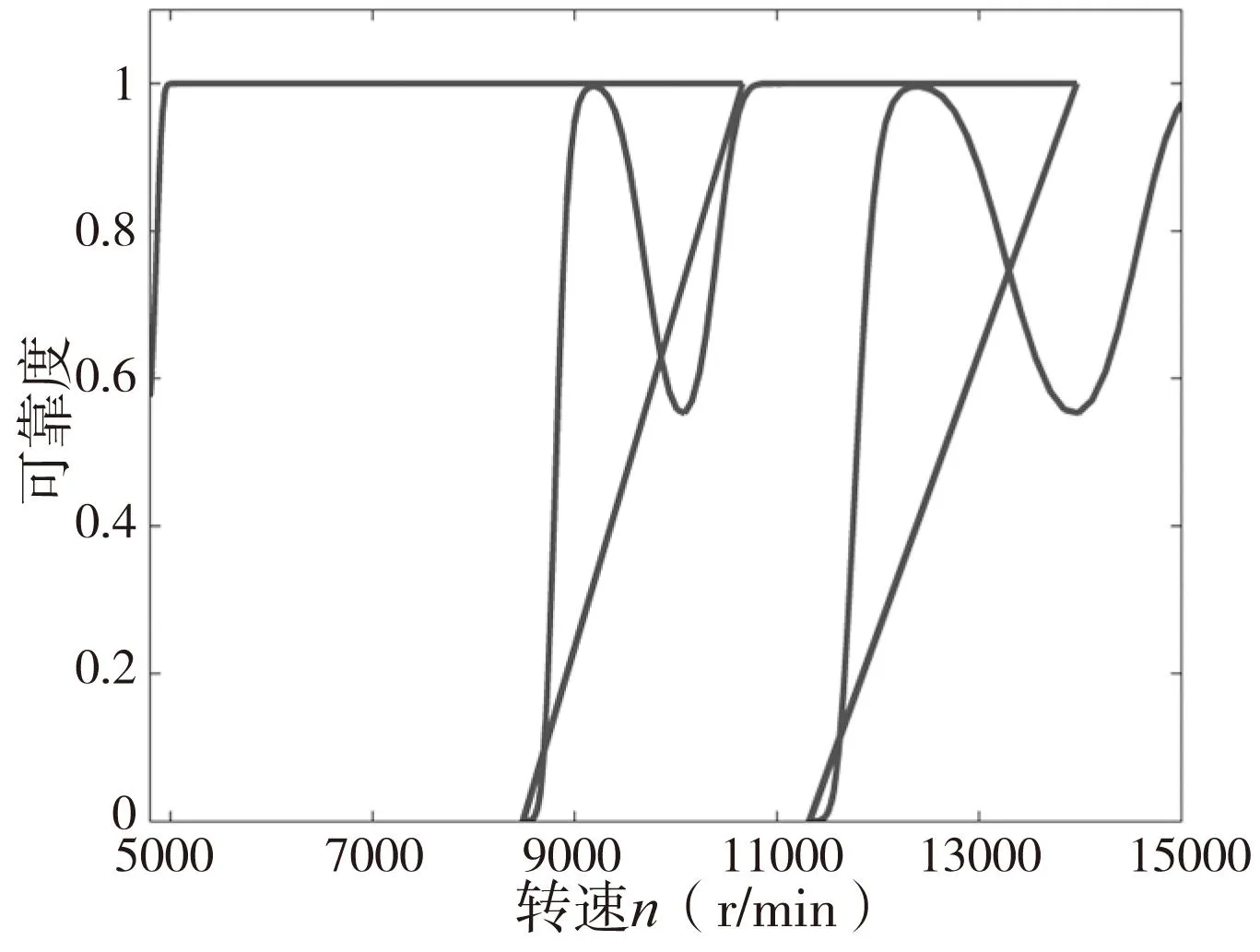
图10　铣削系统刚度均值muK=25000N/mm时的铣削可靠性

4结论

通过数值模拟，分析了各个因素对铣削颤振稳定性的影响，应用MonteCarlo进行铣削颤振可靠度的求解，得到如下结论：

(1)铣削颤振稳定性随铣削系统的阻尼和刚度的增加而增大，随径向铣削宽度和铣削力系数的增加而减小。铣削系统的固有频率对铣削的极限切削深度没有影响，但会使铣削颤振叶瓣图整体右移。

(2)铣削系统刚度的变化不会对铣削颤振可靠度产生影响。

(3)在稳定域按照极限切削深度进行铣削加工时，仅有在特定速度段能够保障不发生颤振现象，且增加铣削系统阻尼可容易地得到铣削稳定域所对应的主轴速度。

[参考文献]

[1] Grossi N, Sallese L, Scippa A, et al. Chatter Stability Prediction in Milling Using Speed-varying Cutting Force Coefficients[J]. Procedia CIRP. 2014, 14: 170-175.

[2] Peng Z K, Jackson M R, Guo L Z, et al. Effects of bearing clearance on the chatter stability of milling process[J]. Nonlinear Analysis: Real World Applications, 2010, 11(5): 3577-3589.

[3] J Tlusty, M Polacek.The stability of the machine tool against self-excited vibration in machining[J]. Proceedings of the ASME International Research in Production Engineering,1963: 465-474.

[4] S A Tobias, W Fishwick.The chatter of lathe tools under orthogonal cutting conditions[J].Transactions of the ASME ,1958 (80): 1079-1088.

[5] Altinta. Analytical Prediction of Stability Lobes in Milling[J]. CIRP Annals - Manufacturing Technology. 1995, 44(1): 357-362.

[6] 迟玉伦，李郝林. 铣削颤振稳定域叶瓣图确定方法研究[J]. 振动与冲击,2014(4): 90-93.

[7] 汤爱君，刘战强. 铣刀参数对薄壁零件铣削稳定性的影响[J].华南理工大学学报(自然科学版), 2009, 37(2): 29-34.

[8] 乔晓利，祝长生. 基于内置力执行器的铣削颤振的主动控制[J]. 机械工程学报,2012,48(1): 185-192.

[9] 李茂月，韩振宇，富宏亚，等. 基于开放式控制器的铣削颤振在线抑制[J]. 机械工程学报,2012, 48(17): 172-182.

[10] Hung J, Lai Y,et al. Analysis of the machining stability of a milling machine considering the effect of machine frame structure and spindle bearings: experimental and finite element approaches[J]. The International Journal of Advanced Manufacturing Technology. 2013, 68(9-12): 2393-2405.

(编辑赵蓉)

Investigation of the Milling Chatter and its Probability

FENG Ji-lu，SUN Zhi-li，SUN Hong-zhe，CHAI Xiao-dong

(School of Mechanical Engineering & Automation, Northeastern University, Shenyang 110819, China)

Abstract：The analytical method was applied to account for the influence of the damping ratio，stiffness，natural frequency，radial milling width and milling force coefficient on the milling stability by the dynamical model of milling chatter. Taking the randomness above parameters into consideration，the Monte Carlo methoad was used to explain the milling chatter reliability in the different damping ratios and stiffness.Current results show that the relationship between the spindle speed and milling chatter reliability is clearly nonlinear. The increasing stiffness of milling system has no effect on the milling chatter reliability. The chatter phenomenon just only can not be occurred in the specific speed zone when machining at the zone of milling stability，which associated with the spindle speed can be easily obtained by increasing the damping ratio of milling system.

Key words：milling chatter;limit cutting depth;reliability;Monte Carlo

中图分类号：TH166;TG506

文献标识码：A

作者简介：冯吉路(1988—)，男，天津人，东北大学博士研究生，研究方向机床主轴动力学及加工动力学，(E-mail)fengjilu123@sina.com; 孙志礼(1957—),男,山东巨野县人,东北大学教授，博导，研究方向为高档数控机床性能分析与可靠性设计。

*基金项目：国家科技重大项目(2013ZX04011-011)

收稿日期：2015-03-02

文章编号：1001-2265(2015)12-0008-04

DOI:10.13462/j.cnki.mmtamt.2015.12.003