＊颅内动脉瘤支架柔顺性能有限元分析

郑清丽，韦明堂，由 衷，安美文，1b，李志强，1b

（1．太原理工大学a．应用力学与生物医学工程研究所，b．材料强度与结构冲击山西省重点实验室，太原030024；

2．英国牛津大学工程科学系，牛津OX1 3QR）



＊颅内动脉瘤支架柔顺性能有限元分析

郑清丽1a，韦明堂1a，由 衷2，安美文1a，1b，李志强1a，1b

（1．太原理工大学a．应用力学与生物医学工程研究所，b．材料强度与结构冲击山西省重点实验室，太原030024；

2．英国牛津大学工程科学系，牛津OX1 3QR）

摘 要：设计一种新型镍钛合金颅内动脉瘤导流支架，采用有限元方法研究了6种具有不同表面筋宽度、厚度和内弧半径的非对称支架模型，系统分析了在弯曲状态下几何参数对其最大等效单轴拉应变及纵向柔顺性的影响，并与Neuroform3颅内支架和PED（pipeline embolization device）支架进行比较分析。结果显示：在弯曲过程中，该支架最大等效单轴拉应变很小，始终处在镍钛合金可恢复应变范围内；最大等效单轴拉应变及弯矩随着支架筋宽度和内弧半径增加而增大，筋厚度对弯曲性能的影响较小；支架柔顺性优于Neuroform3支架和PED支架，能顺利到达目标血管，合理的支架设计对脑动脉瘤血管重建至关重要。

关键词：颅内动脉瘤；导流支架；有限元分析；纵向柔顺性

脑动脉瘤是指脑动脉内腔的局限性异常扩大所导致的动脉壁的一种瘤状突出，具有高发病率和致命率，目前治疗方法有开颅动脉瘤夹闭术和血管内弹簧圈栓塞术［1－2］。开颅动脉瘤夹闭术是一种具有侵入性和技术上相对复杂的操作过程，伴随着很高的风险性。至于血管内弹簧圈栓塞术，由于近年来血管内介入治疗材料科学、介入放射科学、颅内血管内治疗技术的发展，特别是出现了remodeling技术、三维弹簧圈篮筐技术、球囊辅助技术，尤其是颅内专用支架（如Neuroform支架，Leo支架以及Enterprise支架等）广泛使用，在一定程度上改变了动脉内及瘤颈处的血流动力学，降低了动脉瘤的复发率，使绝大多数复杂颅内动脉瘤治疗成为可能［3－5］。随着血管内支架的应用，血管重建也开始被重视，它能够使动脉瘤部位血管恢复到正常的生理结构，变“动脉瘤囊内治疗”为“载瘤血管重建”的治疗理念也逐步形成［6］。根据目前研究，使用脑动脉瘤导流支架是一种有效的方法，其发病率和死亡率在可接受的范围内［7－8］。为此本文提出一种新型镍钛合金颅内动脉瘤导流支架，从实际情况出发建立有限元模型，比较非对称结构模型在不同表面筋宽度、厚度和圆弧半径条件下其最大等效单轴拉应变及纵向柔顺性。

1　计算模型与方法

1．1 几何模型

新型导流支架是由镍钛合金薄壁管经激光切割通过连接键构成的管网状结构。由于支架在本文受力过程中无塑性应变，考虑到计算效率，可取其一部分作为研究对象。支架的几何模型（图1）由以下5个参数进行控制，分别是决定支架周长的半径R0、支架筋宽度w、厚度t、支架表面圆弧部分半径r及

图1　支架的几何模型Fig．1 Geometry model of the stent

相邻筋间的最小距离d。本文取支架半径R0均为1．9mm，最小距离d为0．05mm，通过不同参数w、t和r来研究其对支架柔顺性能的影响，支架模型几

何参数具体数值见表1。

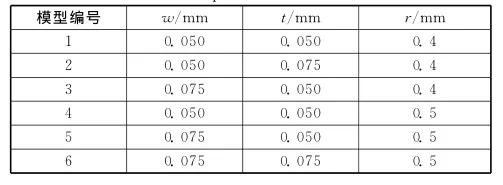
表1　支架模型几何参数Table 1 Geometric parameters of the stent models

1．2 有限元模型

根据模型几何图形特殊性，为保证计算结果精确性，防止由于划分网格产生网格畸变而导致计算过程难以顺利进行，导流支架有限元模型由UG （Unigraphics NX）、MATLAB软件包及ABAQUS／Standard有限元分析软件三者共同完成，通过UG软件包进行三维实体侧面展开图建模，在ABAQUS中进行网格划分，之后在MATLAB软件包中对网格节点进行坐标转换，最终导入ABAQUS有限元分析软件中进行计算。每个模型网格均采用C3D8R且模型筋宽度和厚度方向应至少划分三层网格以确保其精确度。采用超弹性镍钛合金材料，其应力－应变曲线如图2所示。通过嵌入ABAQUS内置的用户子程序来定义材料属性［10］，相关参数见表2。

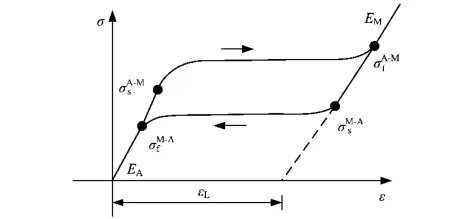
图2　镍钛合金超弹性应力－应变曲线示意图Fig．2 Stress－strain curve of nitinol super－elastic alloys

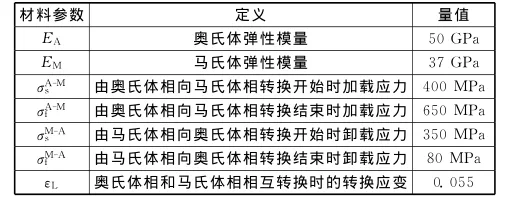
表2　镍钛合金材料性能参数Table 2 Material properties of nitinol

1．3 载荷和边界条件

本文主要研究支架在弯曲过程中，各参数对其最大等效单轴拉应变及纵向柔顺性的影响。以全局坐标轴x轴作为支架中心轴，两端中心轴处各设一参考点（P1，P2）。通过刚体约束将参考点与端部节点6个自由度联系起来，在两端参考点绕z轴各施加90°角位移，分析支架在弯曲状态下的受力情况。具体边界条件如下：

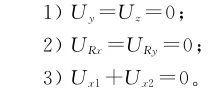
由于在弯曲过程中，曲率达到一定值时支架内侧相互接触，故选择自接触为其接触条件。

2　结果与讨论

2．1 支架在不同弯曲方向下的柔顺性

纵向柔顺性是衡量支架的一个重要因素，柔顺性好的支架能够在错综复杂的血管中协同工作而不会失稳。文中支架是非对称结构，为了更全面地了解支架柔顺性能，以模型4为例，从3个角度（图3）对支架进行弯曲对比分析。其中，状态A为支架在弯曲时，连接键位于支架最下端；B为A状态下反向弯曲；C在A的基础上绕中心轴（x轴）顺时针旋转45°后进行弯曲。3种状态下弯矩－曲率曲线如图4所示。

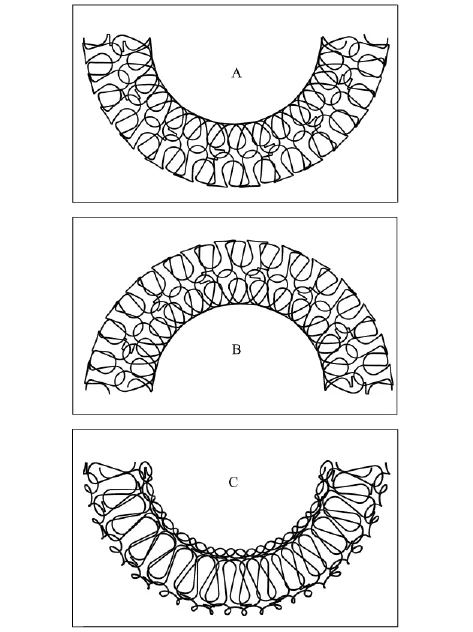
图3　模型4的三种弯曲状态Fig．3 Three kinds of bendings of the model 4

经分析，图3中3种弯曲状态下的弯矩涵盖了支架的最大和最小弯矩。从图4可以看出，支架处于A和B状态下，弯矩－曲率曲线基本完全重合；相同曲率条件下，C状态下的弯矩小于前两种，说明在C状态下，支架的柔顺性更好。对于同一支架，相同曲率、不同弯曲状态下弯矩大者柔顺性差。故为了更有力地说明支架的柔顺性，下文所探讨的支架模型均在A状态下进行弯曲。

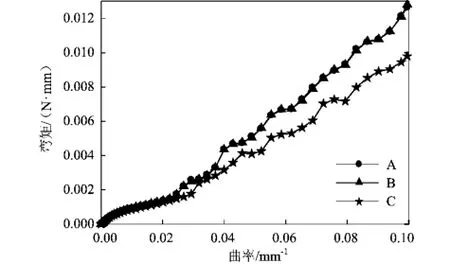
图4　模型4的弯矩－曲率曲线图Fig．4 Bending moment－curvature curves of the model 4

2．2 支架最大等效单轴拉应变

对于自膨式导流支架来说，最大等效单轴拉应变在8%范围内，即可确保镍钛合金支架弯曲后材料未进入塑性状态。表3给出了在弯曲状态下支架模型最大等效单轴拉应变。

表3　最大等效单轴拉应变εmaxTable 3 Maximum equivalent uniaxial tensile strainεmax

从表3中可以看出，支架在弯曲状态下最大等效单轴拉应变εmax均远小于8%，完全处于镍钛合金可恢复应变范围内。支架弯曲过程是通过图1中间距d的增大带动支架中性轴以下圆弧部分张开来实现的。比较模型1和3、模型4和5可知，t和r相同时，模型3的εmax是模型1的1．85倍，模型5是模型4的1．8倍；说明w较大者其εmax也相应增大，因此弯曲过程中，宽度w可作为抵抗支架弯曲变形的主要参数。对比模型1和2、5和6可知，w和r相同时，t大者相应的εmax略有增加；这是因为支架在发生弯曲变形时，其圆弧部分所受的弯矩方向大致垂直于宽度w方向，而平行于厚度t方向，基于初等梁理论，t对εmax影响甚微，不作为其关键参数。从模型1和4、3和5可以看出，随着支架几何参数r的增加，εmax增大，故r也是支架弯曲过程中εmax需考虑的一个重要参数。

2．3 支架柔顺性

从图3支架绕z轴弯曲状态下应变云图中可以看出，相对转角为180°时，支架仍然处于良好的工作状态。图5列出了6种模型支架的弯矩－曲率曲

线图。

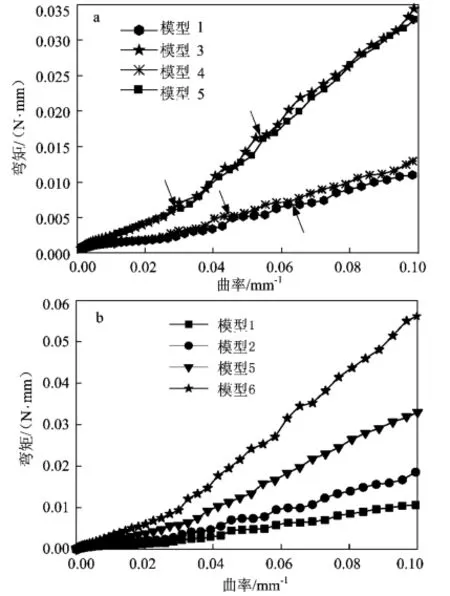
图5　弯曲状态下支架的弯矩－曲率曲线Fig．5 Bending moment－curvature curvesof the stents under bending

从图5中发现，支架模型在图中箭头所标示处均出现曲率增加弯矩却几乎不变的现象，这是由于镍钛合金中应力诱发马氏体相变过程伴随产生滞后效应。图5a中模型1和3、4和5分别具有相同的t 和r，随着支架宽度w增加，弯矩增加幅度较大，其柔顺性变差。当曲率为0．1时，模型3的弯矩是模型1的3．26倍；模型5是模型4的2．67倍；由此可看出宽度w对支架柔顺性的影响较大。模型1和4、3和5的弯矩－曲率曲线很接近，说明了t对支架纵向柔顺性的影响很小，原因与之前描述的支架圆弧部分所受的弯矩方向大致垂直于宽度w方向，而平行于厚度t方向是一致的。t对弯矩的影响甚微，这为支架尺寸优化设计提供了依据，即在w和r一定的条件下，通过改变t，在柔顺性变化很小范围内，探讨支架压握和膨胀性能所能达到符合血管支架的最优状态。图5b中模型1和2、5和6分别具有相同的w和t，随着r增加，其柔顺性也变差。当曲率为0．1时，模型2的弯矩是模型1的1．75倍，模型6是模型5的1．67倍；可知r对支架柔顺性也存在一定影响，但相比较宽度w，其影响会略小。

为了评估本文中新型支架的柔顺性，我们以Neuroform3［11］和PED两种支架为参考目标，这两种支架目前均广泛应用于脑动脉瘤的治疗，且具有良好柔顺性。两者半径均与本文中支架半径R0相同，其中Neuroform3支架与模型4具有相同的w、t，PED编织支架所用镍钛合金丝径为0．05mm，编织角度为60°。经有限元计算分析，模型4与两参考支架的弯矩－曲率关系曲线如图6所示。相同曲率下，模型4的弯矩最小，说明在柔顺性方面，模型4

图6　模型4、PED支架和Neuroform3支架的弯矩－曲率曲线Fig．6 Bending moment－curvature curves of the model4stent，the PED stent and the Neuroform3stent

优于Neuroform3和PED两种支架。因此，作为脑动脉瘤导流支架，本文中新型支架满足血管对其纵向柔顺性的要求。

3　结论

1）弯曲过程中，6种支架模型的最大等效单轴拉应变εmax均小于8%，在其材料可恢复应变范围内。支架筋宽度w和圆弧半径r决定着支架最大等效单轴拉应变，模型构造中厚度t对其影响却很小。

2）支架筋宽度w和圆弧半径r越小，柔顺性越好，其中筋宽度w对其影响尤为明显；厚度t对支架柔顺性影响很小，不作为主要因素，这为后续我们对支架的进一步优化设计提供依据。

3）与Neuroform3和PED两种支架相比，在相同条件下，本文所研究的支架柔顺性优于以上两种支架，说明该新型支架在柔顺性方面作为治疗脑动脉瘤支架具有一定的实用性。

参考文献：

［1］ Brisman J L，Song J K，Newell D W．Medical progress：cerebral aneurysms［J］．New England Journal of Medicine，2006，355：928－939．

［2］ Linfante I，Wakhloo A K．Brain aneurysms and arteriovenous malformations advancements and emerging treatments in endovascular embolization［J］．Stroke，2007，38（4）：1411－1417．

［3］ Linn F H H，Rinkel G J E，Algra A，et al．Incidence of subarachnoid hemorrhage：role of region，year and rate of computed tomography：a meta－analysis［J］．Stroke，1996，27：625－629．

［4］ 王志锁，王宏磊．Enterprise支架在颅内动脉瘤栓塞中的应用研究［D］．长春：吉林大学，2013．

［5］ 朱旭成，魏建军．Neuroform支架在颅内宽颈动脉瘤中的临床应用研究［D］．合肥：安徽医科大学，2010．

［6］ 刘建民，黄清海．血管内支架在脑动脉瘤治疗中的价值［J／EB］．中华脑血管杂志：电子版，2009，3（1）：1－3．

［7］ Lubicz B，Collignon L，Raphaeli G，et al．Flow－diverter stent for the endovascular treatment of intracranial aneurysms：aprospective study in 29patients with 34aneurysms［J］．Stroke，2010，41（10）：2247－2253．

［8］ Pierot L．Flow diverter stents in the treatment of intracranial aneurysms：Where are we？［J］．Journal of Neuroradiology，2011，38（1）：40－46．

［9］ McKelvey A，Ritchie R．Fatigue－crack propagation in nitinol，a shape－memory and superelastic endovascular stent material［J］．Journal of Biomedical Materials Research，1999，47（3）：301－308．

（编辑：张红霞）

［10］ Kusy R P，Whitley J Q．Effects of surface roughness on the coefficient of friction in modern orthodontic systems［J］．Biomechanics，1990，23（9）：913－925．

［11］ Ma Jiayao，You Zhong，James Byrne，et al．Design and mechanical properties of a novel cerebral flow diverter stent［J］．Annals of Biomedical Engineering，2014，42（10）：960－970．

?

ZHENG Qingli1a，WEI Mingtang1a，YOU Zhong2，AN Meiwen1a，1b，LI Zhiqiang1a，1b
（1．a．Institute of Applied Mechanics and Biomedical Engineering；b．Shanxi Key Lab．of Material Strength ＆Structural Impact，
Taiyuan University of Technology，Taiyuan030024，China；
2．Department of Engineering Science，University of Oxford，Oxford OX1 3QR，UK）

Abstract：A novel nitinol flow diverter stent of intracranial aneurysms has been investigated under bending．Finite element analysis has been conducted to study the maximum equivalent uniaxial tensile strain and longitudinal flexibility of six asymmetric stent models with different strut width，thickness，and inner radius of the arc．Compared with Neuroform3stent and Pipeline Embolization Device（PED），the results show that，in the process of bending，the stent has a small maximum equivalent tensile strain within the range of the recoverable strain of the nitinol．The maximum equivalent uniaxial tensile strain and bending moment both increase with the width and arc radius of strut，while the thickness has a negligible effect on the bending．Superior to the Neuroform3stent and PED in flexibility，the novel stent can access to target blood vessels smoothly．Reasonable design of the stent is essential for the treatment of cerebral aneurysms revascularization．

Key words：cerebral aneurysm；flow diverter stent；finite element analysis；longitudinal flexibility

作者简介：郑清丽（1986－），女，山西运城人，硕士生，主要从事固体力学研究，（E－mail）qingli＿522＠126．com

基金项目：山西省“百人计划”专家资助项目：在放置支架后的颅内动脉瘤演变；国家自然科学基金资助项目（11372208）

收稿日期：＊2014－09－15

文章编号：1007－9432（2015）03－0352－05

DOI：10．16355／j．cnki．issn1007－9432tyut．2015．03．021

文献标识码：A

中图分类号：R318．01

通讯联系人：由衷（1963－），博士，教授，博导，（Tel）0351－6018226，（E－mail）zhongyou＠eng．ox．ac．uk