某型履带车辆诱导轮结构强度分析

朱兴高，顾 亮（北京理工大学机械与车辆学院，北京100081）



某型履带车辆诱导轮结构强度分析

朱兴高，顾 亮
（北京理工大学机械与车辆学院，北京100081）

摘 要：为配合某型履带车辆轻量化研制工作，研究分析了诱导轮所受履带张紧力的大小、方向以及位置，验证了诱导轮结构设计的合理性。建立了诱导轮的有限元模型，并进行结构强度的计算，对计算结果进行分析比较。结果表明，诱导轮的最大应力值位于包角为145°的轮毂边缘和部分加强筋处，小于材料的许用应力，满足设计要求。本研究为诱导轮的轻量化优化设计提供依据。

关键词：履带车辆诱导轮；应力应变；结构强度分析；有限元法

（E－mail）zhuxinggao2008＠126．com，（Tel）18810328092

通讯联系人：顾亮，男，教授，博导，主要从事振动与噪声控制、车辆智能悬挂研究，（E－mail）guliangbit＠gmail．com

履带装甲车辆的行动系统作为整车的重要组成部分，其性能的好坏直接影响到车辆性能的发挥。随着我国军用履带装甲车辆的不断发展，车辆行动系统零部件结构强度和轻量化的设计分析已经成为重要的研究内容。在以往的结构设计中，设计人员基本上将注意力集中在行动系统的通过性和减振性能上，而往往忽略行动系统零部件结构强度分析和轻量化设计。履带车辆行动系统的质量占到整车质量的20%以上，开展车辆行动系统零部件的结构强度分析和轻量化设计是我国履带装甲车辆业界的重点［1］。诱导轮是车辆行动系统中的关键件之一，其功用是用来支撑上支履带段和改变上支履带段的运动方向［2］。诱导轮安装在履带张紧机构的曲臂轴上，靠张紧机构移动诱导轮来张紧和调节履带的松紧度［3］。分析诱导轮所受载荷的情况，计算诱导轮的结构强度，可以为履带车辆行动系统的设计提供理论依据，并为今后进一步可靠性研究及实测试验奠定基础。

1　诱导轮三维几何模型

诱导轮按轮缘的数量分为单排和双排诱导轮，按减振程度分有全金属（无减振）诱导轮、内部减振诱导轮和外部减振（外橡胶圈）诱导轮。诱导轮轮盘的支撑体是由多个“T型”筋组成，“T型”筋之间设计有多个具有排泥和减重功能的扇形孔。由于其采用铝制材料，强度相对较低，需对其进行强度计算，分析其能否满足要求［4］。本文研究为双排外部减振诱导轮，利用建模软件CATIA建立诱导轮三维几何模型见图1所示；诱导轮几何参数及质量属性见表1所示。

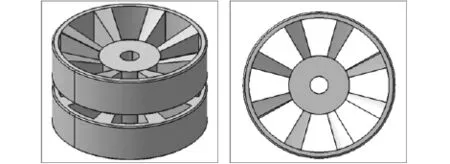
图1　诱导轮三维几何模型

表1　诱导轮几何参数及质量属性

2　诱导轮有限元模型建立

把三维几何模型导入Hypermesh软件中，建立有限元分析模型，主要内容包括几何模型的简化和离散、模型导入和材料特性的定义、单元类型的选择和网格划分、边界条件处理以及载荷条件处理。

2．1 几何模型的简化和离散

由于软件之间的接口技术问题，在进行模型的导入时，有可能发生几何特征丢失或者产生一些不必要的小碎面，这些几何错误都需要进行清理，否则会导致网格无法划分，影响计算的精度和速度，严重时可能会造成计算无法收敛［5］。针对上述问题，具体解决方法有：对模型中的微小几何特征进行简化；对较为复杂的CAD模型，可以利用几何清理工具来实现面的缝合、修补或合并，以及重新划分、线的压缩、相邻点的合并。由于本文计算模型结构简单，简化过程只是删除了对应力计算影响较小的倒角和外部的橡胶轮缘，其他的结构并未改动。诱导轮由多个面构成，很难全部直接用规则的六面体单元划分网格，因此诱导轮比较适合用四面体单元划分自由网格。将诱导轮离散为一系列单元，各单元在节点处相联，相邻单元之间通过公共节点传递力和力矩。模型共计146 728个节点和633 705个单元，诱导轮有限元离散模型和局部放大图如图2所示。

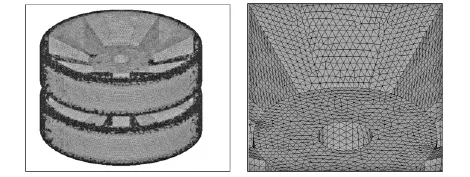
图2　诱导轮有限元离散模型和局部放大图

2．2 材料特性

诱导轮材料采用铝合金LD10，材料特性见表2。

表2　诱导轮材料特性

2．3 边界条件和施加载荷2．3．1 边界条件处理

诱导轮通过轮毂和轴承安装在履带张紧机构的曲臂轴上，因此可以对诱导轮内孔表面的所有节点施加约束。

2．3．2 载荷的处理

计算诱导轮附近的履带张紧力。诱导轮、诱导轮曲臂和履带张紧机构见图3所示。其中，P1是诱导轮曲臂的回转中心，它固定在车体上；诱导轮与诱导轮曲臂通过P2铰接在一起，而P3为诱导轮曲臂与履带张紧装置的铰接点；Pt为履带张紧装置的回转中心，它与车体通过铰链连接在一起；履带张紧装置的长度PtP3可以调节，进而影响P3、P2点即诱导轮的位置，从而调节诱导轮附近的履带张紧力［6－7］。为了换算到诱导轮轮缘上的履带张紧力，必须建立诱导轮－履带段系统的动力学模型，分析诱导轮、诱导轮曲臂及履带张紧装置之间的几何关系。取诱导轮－履带段系统为研究对象，得到诱导轮－履带段系统的受力分析图，见图4所示。

图3　诱导轮和履带张紧机构

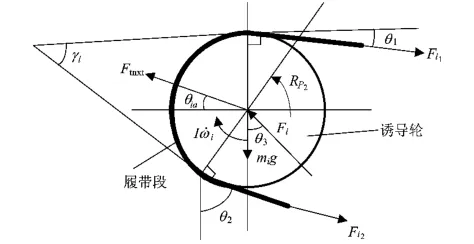
图4　诱导轮－履带段系统受力分析图

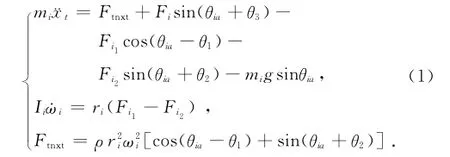
忽略诱导轮转动时产生的摩擦力矩，则诱导轮的动力学平衡方程为：式中：mi为诱导轮质量；¨xt为诱导轮轮心处的位移；Fi为诱导轮曲臂作用于诱导轮上的作用力；Ftnxt为履带转动时产生的离心力；Fi1，Fi2分别为诱导轮轮缘履带包角处的履带张紧力；g为重力加速度；RP2为诱导轮旋转时产生的摩擦力矩；ri为诱导轮半径；Ii为诱导轮转动惯量；ωi为诱导轮转动加速度；ρ为单位长度的履带质量；θ1为诱导轮上轮缘履带张紧力Fi1与诱导轮轮心水平面的夹角；θ2为诱导轮下轮缘履带张紧力Fi2与诱导轮轮心垂直面的夹角；θ3为诱导轮曲臂作用于诱导轮上的作用力Fi与诱导轮轮心垂直面的夹角；θia为履带转动时产生的离心力Ftnxt与诱导轮轮心水平面的夹角。

取诱导轮曲臂为隔离体，得到诱导轮曲臂的几何关系及受力分析图，如图5所示。

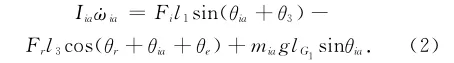
诱导轮曲臂转动时产生的摩擦力矩较小，可以略去不计，则诱导轮曲臂满足动力学方程：式中：点G为诱导轮曲臂重心点；Fr为履带张紧器产生的张力；RP1，RP2，RP3为诱导轮曲臂转动时在

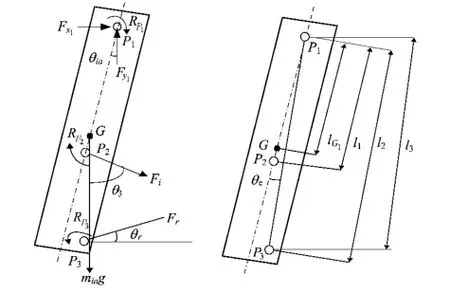
图5　诱导轮曲臂隔离体几何及受力分析图

点P1，P2，P3处产生的摩擦力矩；Iia为诱导轮曲臂转动惯量；ωia为诱导轮曲臂转动加速度；Fi为诱导轮作用于诱导轮曲臂上的作用力；l1为诱导轮曲臂回转中心到诱导轮与诱导轮曲臂铰接点的距离；l3为诱导轮曲臂回转中心到诱导轮曲臂与履带张紧装置的铰接点的距离；θe为诱导轮曲臂回转中心到诱导轮曲臂与履带张紧装置的铰接点与诱导轮曲臂几何体中心线的夹角；mia为诱导轮曲臂的质量；lG1为诱导轮曲臂回转中心到诱导轮重心的距离；Fx1和Fy1为诱导轮曲臂回转中心处水平和垂直方向的分力。

动力学方程（1）和（2）中含有多个变量，可以利用各构件之间的几何关系来求解。根据诱导轮几何参数、诱导轮曲臂的位置以及履带张紧装置的几何尺寸，诱导轮轮缘处履带张紧力Fi1、Fi2可以表示为：

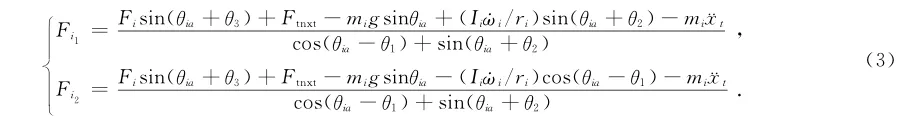
由方程（2）可以得到Fi的表达式为：

把公式（4）代入公式（3）得：

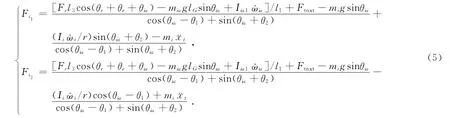
诱导轮轮缘处履带张紧力Fi1、Fi2的计算与履带张紧装置PtP3的长度、履带张紧器张力Fr、诱导轮曲臂角速度ωia等因素有关。由于履带张紧装置多为液压驱动，诱导轮曲臂的加速度¨xt很小，可略去不计；并且，在履带车辆行驶时，惯性项的幅值较小，也略去不计，则诱导轮轮缘处的履带张紧力可以表示为

Fi1≈Fi2＝［Frl3cos（θr＋θe＋θia）－miaglGsinθia］／l1＋Ftnxt－migsinθia

cos（θia－θ1）＋sin（θia＋θ2

）

．

（6）

履带车质量30t，诱导轮的质量为100kg，根据现有参考资料［4，8－9］，屈服极限的储备系数应该不小于3。取履带车辆诱导轮的动载荷系数为3，履带张紧器产生的张力即履带预张紧力为30kN，求得Fi1≈Fi2＝573 300N。

如图4所示，Fr＝2Fi1cos（γl／2）。其中，Fr为换算到诱导轮轮缘上的履带张紧力；γl为履带上支段与倾斜段之间的角度，π－γl为诱导轮履带包角［4］。该诱导轮履带包角为145°，因此γl＝35°，则Fr＝1 093 531N。按照上述分析计算结果，在诱导轮轮缘145°包角接触面积处施加力载荷，均布在单元节点上。诱导轮的有限元模型如图6所示。

图6　诱导轮有限元模型

3　诱导轮结构强度计算

根据有限元模型中建立的约束和载荷，在有限元分析软件hypermesh中对诱导轮进行结构强度计算，得到诱导轮的变形和应力分布云图，见图7和图8所示。从中可以看出，最大应力值及其出现的位置，以及诱导轮的应力分布和变形情况。

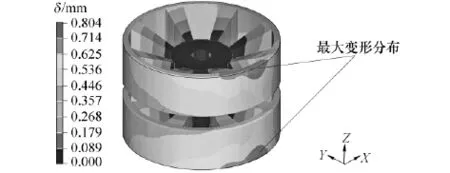
图7　诱导轮变形分布云图

图8　诱导轮应力分布云图

最大等效应力位于145°包角部分和加强筋靠近轮毂处，最大应力为260MPa，小于材料的屈服极限315 MPa，满足材料强度要求；最大变形量为0．803 6mm，出现在145°包角中心边缘处，变形不大，满足刚度设计要求。

4　结束语

本文建立了诱导轮几何模型，采用四面体单元建立了诱导轮的离散化模型，通过实际工况对诱导轮进行加载计算，得到诱导轮变形和应力分布状况。结果表明，诱导轮在包角和加强筋靠近轮毂处出现应力最大值260 MPa，小于材料的屈服极限315 MPa。其数值较大主要原因是建立有限元模型时忽略了履带板和诱导轮轮缘处的减振橡胶，动载荷系数取3．0足以满足设计要求。采用有限元法来分析诱导轮的结构强度，为诱导轮的轻量化优化设计提供了依据。

参考文献：

［1］ 毛明，庞宝文．坦克装甲车辆技术发展新动向和发展重点［J］．车辆与动力技术，2012（3）：51－55．

［2］ 袁芬，张明．高速履带车辆诱导轮张紧力的计算与仿真［J］．车辆与动力技术，2008（1）：44－48．

［3］ 闫清东．坦克构造与设计［M］．北京：北京理工大学出版社，2007．

［4］ 巴依科夫尤帕沃尔科特阿．履带车辆的设计与计算［M］．北京：北京理工大学出版社，1996．

［5］ 刘荣军，吴新跃，郑建华．有限元建模中的几何清理问题［J］．机械设计与制造，2005（9）：145－147．

［6］ 黄雪涛，顾亮，吕唯唯，等．履带张紧力及其影响因素分析［J］．兵工学报，2014（7）：1110－1118．

［7］ 马星国，潘仕卫，尤小梅，等．履带行驶系统数学模型及张紧力计算［J］．振动与冲击，2014（3）：186－190．

［8］ 王珂晟，刘跃进．重型装备的履带板强度分析［J］．起重运输机械，2009（9）：85－87．

［9］ 段勇军，时社萍．安装架结构强度分析与疲劳损伤评估［J］．电子机械工程，2013（6）：14－17．

（编辑：庞富祥）

Structure Strength Analysis on Idler Wheel of Tracked Vehicle

ZHU Xinggao，GU Liang
（School of Mechanical and Vehicle Engineering，Beijing Institute of Technology，Beijing100081，China）

Abstract：For the lightweight research of some tracked vehicle，the size，orientation and position of idler wheel by track tension were studied to verify the rationality of its structure design．A finite element model of the idler wheel was established and its strength was calculated．The comparison results show that the maximum stress of the idler wheel appears at the wheel edge with cornerite of 145°and some ribs near the hub．Its value is less than the allowable stress of materials，which satisfies the design requirements．The study provides a basis for optimal lightweight design for the idler wheels．

Key words：idler wheel of tracked vehicle；stress－strain；structure strength analysis；finite element method

作者简介：朱兴高（1984－），男，山东沂水人，博士生，主要从事履带车辆设计与理论研究（371323198406049130），

基金项目：国家自然科学基金资助项目：可变形地面－履带板耦合作用特性研究（1030020220707）

收稿日期：＊2015－01－07

文章编号：1007－9432（2015）03－0274－04

DOI：10．16355／j．cnki．issn1007－9432tyut．2015．03．005

文献标识码：B

中图分类号：U260．331