随机振动载荷下发射装置尾罩疲劳寿命分析

2016-11-28刘万远张红波

航空兵器 2016年4期

刘万远+张红波

摘要：针对发射装置尾罩在随机振动试验中可能存在的疲劳破坏问题，采用有限元法对其随机振动疲劳寿命进行了预计。分析了频率响应，得到结构的应力传递函数。结合5A06铝合金的S-N曲线和加速度PSD激励，采用Dirlik法计算了尾罩随机振动疲劳寿命，结果满足随机振动试验的考核要求。

关键词：疲劳寿命；随机振动；尾罩；发射装置；有限元分析

中图分类号： V241.03文献标识码： A文章编号： 1673-5048（2016）04-0078-03

Abstract： For the problem of fatigue failure on launcher trail cover in random vibration test， the random vibration fatigue life is estimated by finite element method. The stress transfer function is obtained by frequency response simulation. Combined with SN curve of 5A06 aluminium alloy and acceleration power spectral density loads， random vibration fatigue life of trail cover is analyzed by Dirlik method. The results meet the requirements of random vibration test.

Key words： fatigue life； random vibration； trail cover； launcher； finite element analysis

0引言

外挂空空导弹大多采用轨式发射装置进行悬挂和发射[1-2]，尾罩是某轨式发射装置的一个重要组成部分，其通过锁钩与发射装置壳体上的挂钩扣合实现固定，以保证挂飞过程的可靠连接[3-4]。发射装置作为飞机外挂物在实际飞行中承受多种复杂环境条件的联合作用[5-6]，其中随机振动载荷对其结构的影响最大，需要特别关注。结构振动疲劳是指结构所受动态交变载荷（如振动载荷等）的频率分布与结构固有频率分布具有交集或相接近，从而使结构产生共振所导致的疲劳破坏现象[7]。

为了确保尾罩在发射装置挂飞过程中的安全可靠，避免发生疲劳破坏，首先应能够准确预估其疲劳寿命，找出振动疲劳的薄弱环节，进而通过结构优化设计，提高抗疲劳特性。本文根据疲劳寿命分析的基本理论，利用有限元方法对尾罩开展了随机振动载荷下的疲劳寿命分析，得出疲劳寿命的大小、分布情况及薄弱环节位置，验证了尾罩结构设计的合理性。

1振动疲劳寿命分析理论

振动疲劳寿命的计算方法分为基于统计计数的时域分析方法和基于功率谱密度的频域分析方法。时域分析方法首先要找出结构的危险点，然后根据危险点的应力（应变）随时间变化的函数关系，得出应力（应变）的幅值和均值，再选取合适的损伤累积理论进行寿命估计[8-9]。该方法计算准确，但数据处理量非常大，有限元分析难以实现，限制了其使用范围。频域分析方法是利用结构危险点的应力功率谱密度函数，运用统计原理获得相应功率谱函数的相关统计参数，同时结合应力幅值的概率密度函数，选取合适的损伤累积理论进行寿命估计[10-12]。该方法因计算简单、无需循环计数而在航空航天等多个领域得到了广泛的应用。

频域分析方法有很多种，其中Dirlik法是最常用的一种，其提供了一种更普遍的方法来确定应力振幅的概率密度函数，适用于任何类型功率谱。 Dirlik法是一个通过模拟“雨流计数”得到应力幅值概率密度函数的半经验公式，由一个指数分布密度函数和两个瑞利分布密度函数叠加而成，计算结果比较接近试验[13-14]。

航空兵器2016年第4期刘万远等：随机振动载荷下发射装置尾罩疲劳寿命分析2随机振动疲劳寿命分析流程

随机振动疲劳预估需要三方面的信息：几何特性、材料特性和疲劳载荷。几何特征主要指模型的应力计算结果；材料特性主要指材料的S-N曲线；疲劳载荷主要指结构受到的加速度PSD激励。利用有限元软件开展随机振动疲劳分析主要分为两个步骤：首先对有限元模型进行频率响应分析，计算模型的应力传递函数；再根据材料的S-N曲线和加速度PSD激励计算模型的疲劳寿命，具体分析流程如图1所示。

图1随机振动疲劳寿命分析流程

3尾罩的有限元模型

该型发射装置尾罩结构简单，主要由尾罩框、三个加强框、尾罩锥及连接框组成，采用固定式结构，通过螺钉和发射架相连，以保护发射架内部组部件，并与飞机机翼外形相协调，形成良好气动外形。根据研究需要，对尾罩模型进行适当简化，利用ABAQUS软件建立的有限元模型如图2所示，其中零件之间有连接关系的地方采用绑定约束，由于尾罩属于薄板结构，利用二次单元对其进行网格划分。激励的输入位置位于连接框的外环面。

尾罩采用钣金+焊接成形，尾罩框和加强框的材料均采用铝合金板5A06 材料，通过查阅文献[15]可知，弹性模量为71 GPa，泊松比为0.32，密度为2 640 kg/m3，材料S-N计算参考曲线如图3所示。

4仿真分析

4.1频响分析

频响分析采用模态叠加法，目的是得到模型的应力传递函数。首先开展模态分析，以获得各阶模态频率和振型，然后在尾罩激励输入位置施加单位加速度载荷进行稳态动力学分析，得到模型在不同频率下对应的应力幅值，为后续开展振动疲劳分析奠定基础。

4.2随机疲劳分析

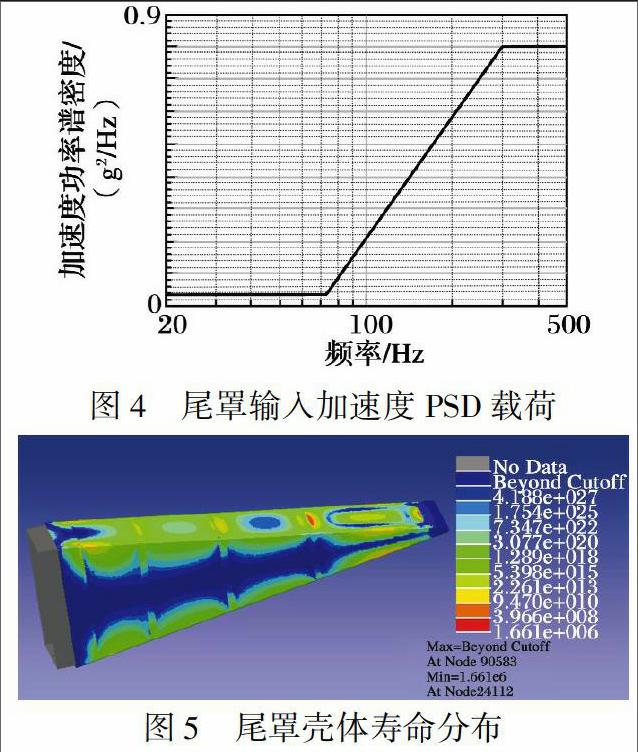
随机疲劳分析需要三方面的信息：应力传递函数、材料S-N曲线和加速度PSD激励。实际分析中，往往只给出了发射装置的加速度PSD激励，且发射装置又包含挂弹和空载两种情况，需要首先对发射装置整体开展挂弹和空载状态随机振动分析，得出尾罩激励面处的随机响应，之后借助数学处理方法对激励面的随机响应进行线性包络，进而得到尾罩的加速度PSD激励，如图4所示。

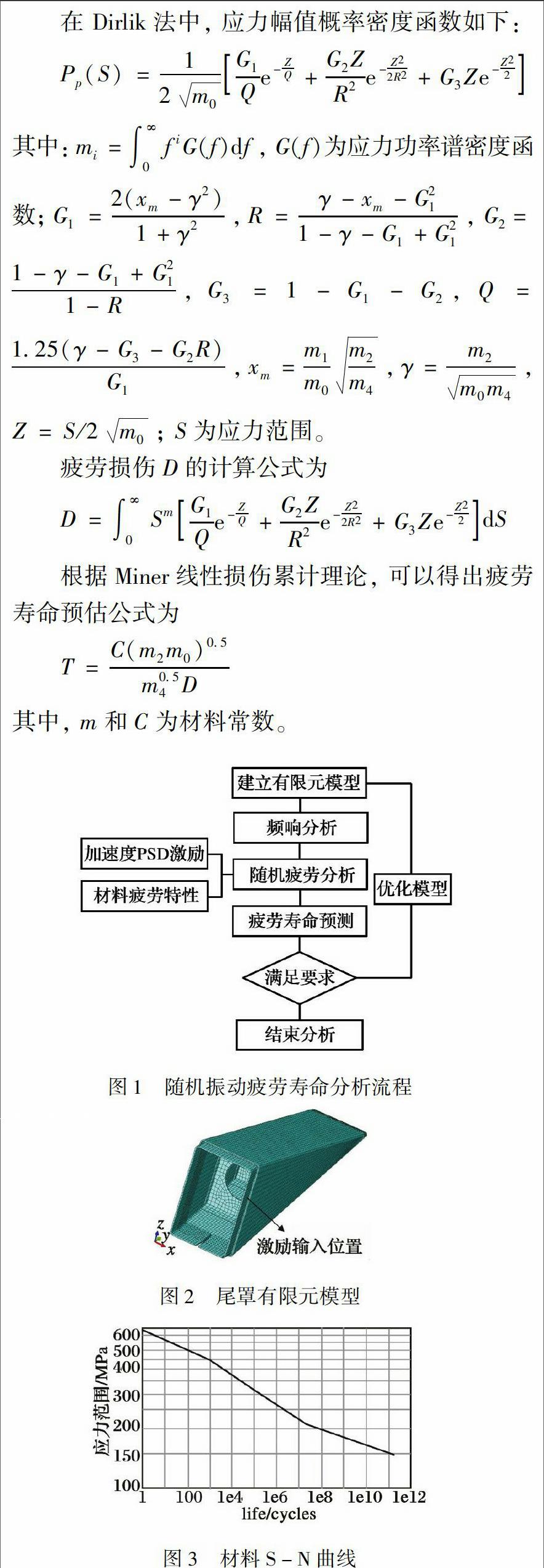
根据频响分析得到应力传递函数、材料S-N曲线和加速度PSD激励，利用疲劳分析软件[16]可开展尾罩的振动疲劳寿命分析。尾罩的疲劳寿命分布云图如图5所示，其寿命最小位置在后加强框顶面对应的尾罩框架上，疲劳寿命值为1.661e6 s，约461.4 h；取4～6的疲劳寿命分析分散系数，尾罩寿命约为77～115.4 h，满足随机振动试验的考核要求。

5结论

研究了频域分析方法中Dirlik法以及疲劳强度理论，针对尾罩在随机振动试验过程中可能存在的疲劳问题，利用ABAQUS和nCode疲劳仿真软件联合开展了疲劳寿命有限元仿真，结果表明尾罩满足随机振动试验的考核要求。仿真工作是在尾罩结构理想情况下开展的，实际加工制造过程中可能存在各种工艺缺陷，譬如焊接缺陷等，均会造成尾罩振动疲劳寿命的减小，在严格控制尾罩生产工艺的基础上，后续要开展相应的环境试验，以验证结果的准确性。本文所述方法可用于机械产品多种方案中不同材料的优选以及结构的优化设计，缩短产品的设计周期，降低试验费用，并为结构随机振动疲劳寿命的研究提供参考和依据。

参考文献：

[1] 郭立峰.轨式发射装置壳体的设计及制造[J].机床与液压， 2012， 40（20）： 4-7.

[2] 鲍华，刘万远.某型发射装置电路板随机振动响应分析[J].航空兵器， 2015（3）： 66-68.

[3] 杨学超，王团.发射装置结构设计与成本控制[J].机械工程师， 2013（1）： 65-67.

[4] 刘刚，关雷.某发射装置尾罩锁钩断裂故障分析[J].四川兵工学报， 2012， 33（4）： 23-24.

[5] 占学红，谢军虎.机载导弹发射装置环境适应性设计初探[J].装备环境工程， 2012， 9（2）： 93-97.

[6] 王清海，刘仲敏，陈小兵.基于Partran/Nastran的发射装置振动特性设计[J].航空兵器， 2011（2）： 52-56.

[7] 姚起杭，姚军.工程结构的振动疲劳问题[J].应用力学学报， 2006， 23（1）： 12-15.

[8] 白春玉，牟让科，马君峰，等.多轴应力响应下结构振动疲劳寿命预估的时域方法研究[J].机械科学与技术， 2013， 32（2）： 289-293.

[9] 刘文光，陈国平，贺红林，等.结构振动疲劳研究综述[J].工程设计学报， 2012， 19（1）： 1-8.

[10] 张坤，薛璞，胡海涛，等.含高频的载荷下飞机薄壁结构振动疲劳寿命分析[J].机械科学与技术， 2012， 31（4）： 639-642.

[11] 管鹏，肖守讷.基于频域的车载污物箱随机振动疲劳寿命仿真[J].机械， 2012， 39（11）： 20-23.