*含参数的Kirchhoff型问题正解的存在性
2015-12-17郭子君张建明王淑丽太原理工大学数学学院太原030024
郭子君,张建明,王淑丽(太原理工大学数学学院,太原030024)
*含参数的Kirchhoff型问题正解的存在性
郭子君,张建明,王淑丽
(太原理工大学数学学院,太原030024)
摘 要:通过变分法,临界点理论以及迭代法研究了一类带参数的Kirchhoff型问题在单位球外这一无界区域上正解的存在性,证明了当参数在一定范围内时,该问题至少存在一个正解。
关键词:Kirchhoff型问题;变分法;迭代法;参数
1 主要结果
本文主要研究以下Kirchhoff型问题的正解和
存在性
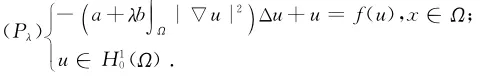
式中:N≥3;Ω:=RN\B1={x∈RN,|x|>1};a,b是正常数;λ≥0是参数。
该问题最初源于如下方程
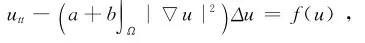
它是由Kirchhoff在文献[1]中研究可伸缩绳自由振动的经典D,Alembert波动方程过程中提出的一种实际存在的方程,早期在文献[2-3]中给出了较为经典的研究。近几年来,许多学者应用变分法以及临界点理论等方法对这类问题在有界区域或者全空间上解的存在性进行了广泛研究[4-12]但关于该问题在无界区域Ω∶=RN\B1上解的存在性的研究相对很少。
笔者主要应用了变分法,临界点理论以及迭代法对Kirchhoff型问题在球外解的存在性进行了探讨,其中迭代法的使用使得问题相对简化。
为了方便叙述本文所得到的主要结果,先给出以下基本假设条件:
1)f∈C(R+,R+),且存在正常数C1,C2>0,使得对于所有t>0,
f(t)≤C1tp-1+C2tq-1成立,式中,p,q∈(2,2*);
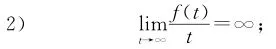
本文的主要结论为:
定理1 若f满足条件1,2,则存在λ*>0,λ∈[0,λ*)时,问题(Pλ)至少有一个正解。
由于本文只考虑问题(Pλ)的正解,故假设当t<0时,f(t)=0.
2 预备知识
H10(Ω)是通常的Sobolev空间,其上的内积和范数分别为
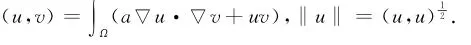
定义H10,r(Ω)={u∈H10(Ω),u径向对称}。由Sobolev嵌入定理1可知H10,r(Ω)是连续的,s∈[2,2*],且存在γs>0使得
定义如下泛函
式中:
由条件1可知,问题(Pλ)的弱解对应于泛函J在H10,r(Ω)中的临界点,且
(2011011002-4,2012011004-3)
对于给定的ω∈H10,r(Ω)和{μk}
12,
[]
1,定义在H10,r(Ω)上的泛函Jω,μk:
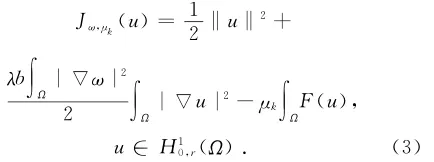
显然
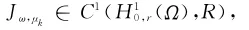
且
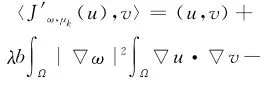
μk∫Ωf(u)v,u,v∈H10,r(Ω).
为了证明问题(Pλ)正解的存在性,需要先前的结论:
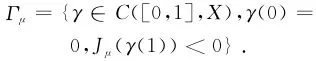
如果对于每一个μ∈I,Jμ(0)=0,Γμ≠且
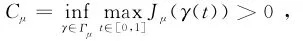
那么对于几乎处处的
μ∈I,存在一个序列{un,μ}X,使得
1){un,μ}是有界的;
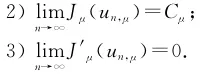
3 结果的证明
由定理2可知,I=
12,
[]
1,空间X=H10,r(Ω),X上相应的泛函为
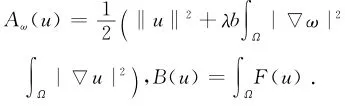
由式(3)定义的泛函Jω,μ就可记为Jω,μ(u)=Aω(u)-μB(u),且
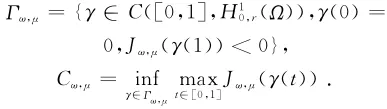
引理1 对于给定的L,R>0以及且ω∈H10,r(Ω)‖ω‖≤R,存在正常数τ=τ(R,L),λ*=λ*(R,L),使得对于所有的μ∈I以及λ∈[0,λ*)有Γω,μ≠,Cω,μ≥τ.
证明 由条件(H1)可知,F(s)≤C1
Psp+C2qsq,s
∈R+.对于u∈H10,r(Ω),由上式及式(1),即可得到
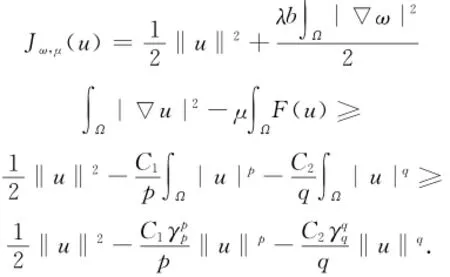
显然存在ρ>0,对于任意的μ∈I,当0<‖u‖<ρ 时Jω,μ(u)>0.尤其是当‖u‖=ρ时,
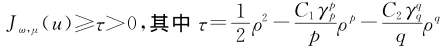
的取值与μ和ω的选取无关。
由条件2易知,对于任意满足M∫Ωφ2>1+L∫Ω|φ|2的M,存在CM>0使得
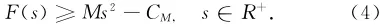
对于给定的L,R>0,定义λ*=aL bR2,取φ∈H10,r(Ω)且φ≥0,‖φ‖=1,suppφ(B2\B1).由式(4)可知,对于任意的μ∈I以及λ∈[0,λ*),
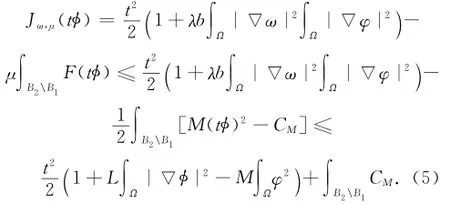
显然,当t→+∞时,Jω,μ(tφ)→-∞.因此,可选取t0>0使得Jω,μ(t0φ)<0.这意味着对于任意的μ∈I以及λ∈[0,λ*),Γω,μ≠φ.
对于固定的μ∈I,由Γω,μ的定义可知,对于任意的γ∈Γω,μ,有‖γ(1)‖>ρ,因为γ(0)=0,由介值定理可知,存在tγ∈(0,1)使得‖γ(tγ)‖=ρ.这样,对于任意的μ∈I以及λ≥0,
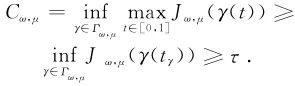
引理2 当λ∈[0,λ*),μ∈I时。泛函Jω,μ有界的(PS)序列有收敛子列。
证明 令{un,ω,μ}H10,r(Ω)是泛函Jω,μ的有界的(PS)序列,即‖un,ω,μ‖≤C,|Jω,μ(un,ω,μ)|≤C,J′ω,μ(un,ω,μ)→0.由于{un,ω,μ}H10,r(Ω)是有界的,
当s∈(2,2*)时,H10,r(Ω)是紧嵌入(见文献[14]推论1.26),即可得到一子列,使得
un,ω,μ弱收敛于uω,μ在H10,r(Ω)上,un,ω,μ(x)→uω,μ(x) 几乎处处在Ω中。
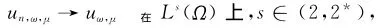
由此可得
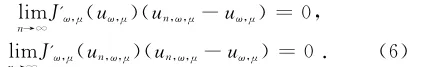
n→∞
根据条件(H1),可知存在Cp,Cq>0使得
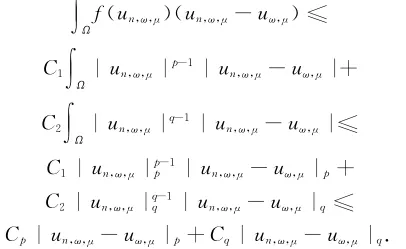
即
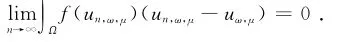
同理可得
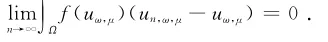
所以
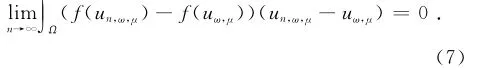
由式(6),式(7)以及
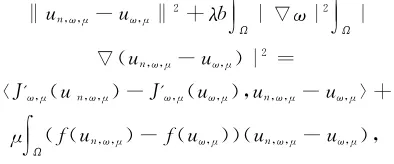
就可得到lim
n→∞.
引理3 令λ∈[0,λ*).那么对于几乎处处的μ∈I,Jω,μ有一非平凡临界点uω,μ.
证明 由定理2可知,
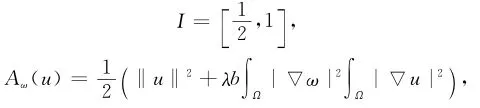
B(u)=∫ΩF(u).
结合引理3可得,对于几乎处处的μ∈I,存在序列
{un,ω,μ}H10,r(Ω)使得
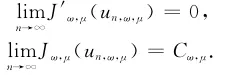
再根据引理2,就可知道存在u∈H10,r(Ω)使得un,ω,μ→uω,μ在H10,r(Ω)上,即n→∞
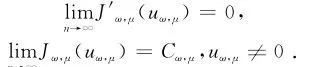
由引理2可知,存在常数C3(L)>0使得t≥0
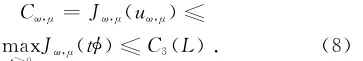
由引理5可知,对于满足μk→1的μk∈I而言,Jω,μk有一非平凡的临界点uω,μk.
引理4 序列{uω,μk}一致有界且Jω,1有一非平凡临界点uω.
证明 因为uω,μk是以下问题的弱解
所以,其所对应的Pohozaev恒等式成立,即
因此
又根据
以及式(8)可得到
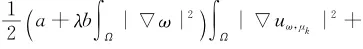
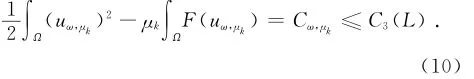
由式(9),式(10)可知
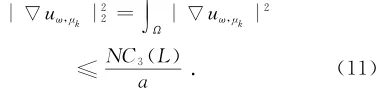
另一方面,由(H1)以及插值不等式可知
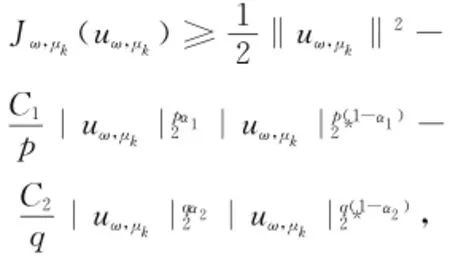
式中:
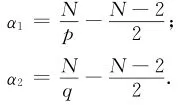
再由式(8)和Sobolev不等式,可知存在常数Cp,Cq>0使得
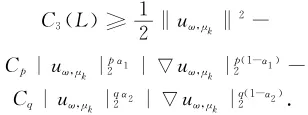
显然pα1<2,qα2<2,结合式(11),可知存在C4(L),使得
∫Ω
(uω,μk)2≤C4(L).(12)
由式(11)和式(12)可推出
‖uω,μk‖2≤NC3(L)+C4(L).(13)
现在证明Jω,1有一个非平凡的临界点。
因为
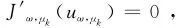
(μk-1)∫Ωf(uω,μk)v,v∈H10,r(Ω).
由(H1),定理2以及μk→1,即可得到J′ω,1(uω,μk)→0.那么{uω,μk}就是Jω,1的一个有界的(PS)序列.由第一步可知,存在uω∈H10,r(Ω)使得uω,μk→uω.
即
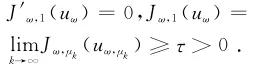
由于Jω,1(0)=0可知uω≠0.
),那么对于任意给定的ω∈H10,r(Ω)满足‖ω‖≤R时,若λ∈[0,λ*),Jω,1有一非平凡的临界点uω且‖uω‖≤R.令ω=u0≡0,那么Ju0,1就有一非平凡临界点并把它记作u1且‖u1‖≤R.再令ω=u1,可知Ju1,1有一非平凡临界点u2且‖u2‖≤R.以此类推,可得到一族
序列{un}H10,r(Ω)且‖un‖≤R是泛函Jun-1,1的非平凡临界点,Jun-1,1(un)≥τ>0,n=1,2,…
现在证明{un}收敛到泛函J的非平凡临界点,因为‖un‖≤R,n∈N,不失一般性,可知存在u∈H10,r(Ω)使得un弱收敛于u在H10,r(Ω)上,un→u在Ls(Ω)上,s∈(2,2*),un(x)→u(x)几乎处处在Ω中.证明方法与(3.4)相同,可得
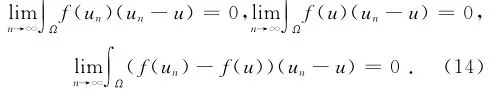
因为
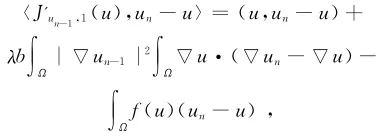
所以
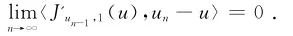
那么
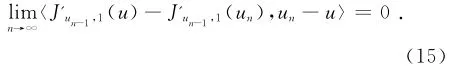
根据式(14),式(15)以及
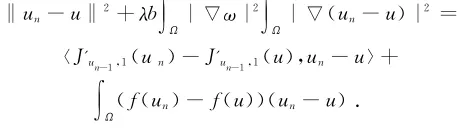
可知
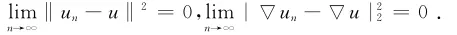
对于任意的v∈H10,r(Ω),有
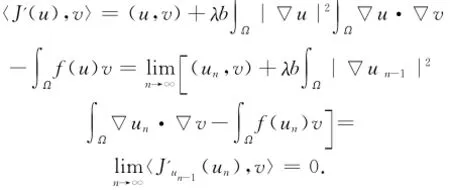
这意味着u是问题(Pλ)的解。
又因为
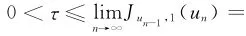
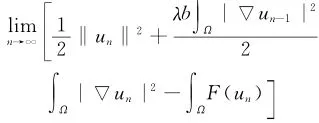
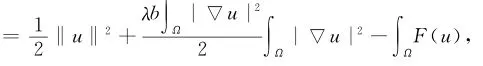
u≠0,所以u是问题(Pλ)的一个正解。
参考文献:
[1] Kirchhoffm G.Mechanik[M].Teubner.Leipzig,1883.
[2] Bernstein S.Sur uneclasses d’équations fonctionnelles aux dérivées partielles[J].Izvestiya Rossiiskoi Akademii Nauk.Seriya Matematicheskaya,1940,4(1):17-26.
[4] 张绍康,熊邵武.Kirchhoff型问题的变号解和多重解[J].昆明学院学报,2010,32(3):16-17.
[5] Autuori G,Pucci P,Salvatori M C.Global nonexistence for nonlinear Kirchhoff systems[J].Arch Ration Mech Anal,2010,196(5):489-516.
[6] 曹小强,孙义静.一类奇异非线性Kirchhoff型问题的正解[J].中国科学院大学学报,2014,31(1):5-9.
[7] Chen C,Song H,Xiu Z.Multiple solutions for p-Kirchhoff equations in RN[J].Nonlinear Anal,2013,86(6):146-156.
[8] Chen S.J,Li L.Multiple solutions for the non homogeneous Kirchhoff equation on RN[J].Nonlinear Anal RWA,2013,14 (3):1477-1486.
[9] Colauonno F,Pucci P.Multiplicity solutions for p(x)-poly harmonic elliptic Kirchhoff equations[J].Nonlinear Anal,2011,74 (17):5962-5974.
[10] Figueiredo G M.Existence of a positive solution for a Kirchhoff problem type with critical growth via truncation argument [J].Math Anal Appl,2013,401(2):706-713.
[11] Júlio F,Corrêa S A,Figueiredo G M.On an elliptic equation of p-Kirchhoff type via variational methods[J].Bull Aust Math Soc,2006,74:263-277.
(编辑:刘笑达)
[12] Kim D,Kim S,Jung I H.Stabilization for the Kirchhoff type equation from an axially moving heterogeneous string modeling with boundary feedback control[J].Nonlinear Anal,2012,75(2):3598-3617.
[13] Jeanjean L.On the existence of bounded Palais-Smale sequences and application to a Landesman-Lazer-type problem set on RN[J].Proc Roy Soc Edinburgh Sect,A,1990,129(4):787-809.
[14] Willem M.Minimax Theorem[M].Birkhuser Boston,1996.
Existence of Positive Solution for a Kirchhoff Type Problem with Parameters
GUO Zijun,ZHANG Jianming,WANG Shuli
(College of Mathematics,Taiyuan University of Technology,Taiyuan030024,China)
Abstract:Variational methods,critical point theory,and iterative techniques were used to study the existence of positive solutions for the Kirchhoff type problems with parameters outside unit ball,an unbounded region.The results prove that the equation has at least one positive solution when the parameter is within a confined range.
Key words:Kirchhoff type problem;variation method;iterative technique;parameters
作者简介:郭子君(1990-),女,山西忻州人,硕士生,主要从事非线性泛函分析的研究,(Tel)18334708439通讯联系人:张建明,副教授,主要从事非线性应理分析研究,(E-mail)tyutzjm@163.com
基金项目:国家自然基金项目:关于微结构的高性能混凝土火灾劣化机理及损伤评估理论研究(51278325),山西省科学基金项目
收稿日期:*2014-11-12
DOI:10.16355/j.cnki.issn1007-9432tyut.2015.03.024
文献标识码:A
中图分类号:O175.2
文章编号:1007-9432(2015)03-0366-05
