基于改进FBS理论的浮筏隔振系统计算方法

游彩霞，张光德，何雪松，胡溧

1 武汉科技大学汽车与交通工程学院，湖北 武汉430081

2 中国舰船研究设计中心，湖北 武汉430064

0 引 言

声隐身性能是潜艇的生命线，其中机械噪声是潜艇声隐身控制的重点，而浮筏隔振技术又是国内外潜艇控制机械噪声的主要技术之一［1-3］。在我国潜艇噪声控制领域，该技术经过多年的理论研究和工程实践，已逐步为众多科研单位所熟悉，并得到了广泛的应用。但长期以来，在方案设计和技术设计中，对浮筏隔振系统隔振效果的评估主要是基于经验，对设计过程中的定量化要求缺乏充分可信的理论计算依据。特别是由于缺乏对于浮筏隔振系统动态特性的高精度计算方法，使得设计者对浮筏隔振设计的结果往往需要依靠最终的样机试验才能得到验证和确认。这种状况一方面会给隔振设计过程带来一定的不确定性，留下风险隐患；另一方面，也使得潜艇机械设备的隔振设计缺乏有效的技术手段支撑，难以得到最为优化的设计方案。特别是在技术设计完成后，若再进行设计方案的更改，将会带来较大的人力和物力的浪费，影响工程进度。

目前，在潜艇隔振工程设计中，迫切需要一套工程实用的高精度浮筏隔振系统动态特性计算方法，能在设计阶段就对潜艇浮筏隔振系统的隔振效果进行快速、有效的定量评估，逐步实现浮筏隔振设计从定性化向定量化设计的转变。

早期的浮筏隔振系统动态特性计算方法主要是基于多刚体动力学理论，其基本的思想是将设备、筏体及基础视为没有弹性和阻尼的刚体，将隔振器视为无质量的弹性阻尼元件［4-5］。使用该方法建模分析方便，计算规模较小，也能反映系统的主要特征，因此在CAE 技术兴起之前，有着广泛的应用。但该方法无法考虑基座及筏体的非刚性特征，其计算精度与工程应用的需求还有一定距离。

目前广泛使用的浮筏隔振系统动态特性计算方法主要是基于有限元理论［6-8］。本质上，浮筏系统的有限元建模与多刚体动力学建模相同，前者仅仅是后者在分析粒度上的细化。正是由于考虑了筏体的弹性变形，有限元建模分析所考虑的系统频带与刚体建模分析相比更宽广，精度也更高。不过，现有的基于有限元的计算方法在处理隔振器时，同样将隔振器视为了无质量的弹性阻尼元件，没能考虑隔振器的质量效应影响，此外，在处理基座的非刚性特征的影响时，也存在技术处理上的困难。

基于频响函数的子结构法（FRF-based Substructure，FBS）是近年来汽车行业中，针对汽车发动机悬置系统动态特性分析需求，提出的一种新型隔振系统计算方法，它融合了阻抗和四端参数理论，并将各子结构单独考虑，能很方便地结合理论及测试数据，同时天然回避了基座模拟上的困难，特别适合具有多个相对独立子结构系统的动态特性计算［9-10］。

本文将基于子结构法原理，针对浮筏隔振系统的特点，利用子结构的频响函数，建立一种适用于浮筏隔振系统动态特性计算的子结构计算方法。并将重点解决现有FBS 方法中仅考虑隔振器的刚度和阻尼特性，而没有计入隔振器质量效应影响的问题，以提升浮筏隔振系统动态特性计算的精度。

1 FBS 基本理论

1.1 单一子结构

图1 所示为某子结构A 的力分析示意图。

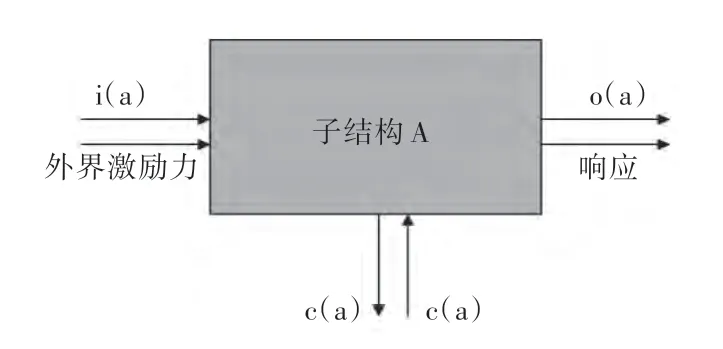
图1 子结构A 力分析示意图Fig.1 The mechanical analysis sketch of substructure A

图1 假设子结构A 的振动速度响应{VA} 为

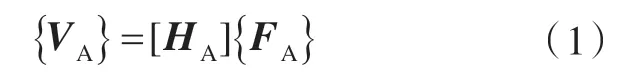
式中：[HA]为传递函数矩阵；{FA} 为外部激励矩阵。考虑到子结构A 与其他子结构的耦合，可将子结构A 分为3 类坐标：激励坐标（下标i）、响应坐标（下标o）以及耦合坐标（下标c），因此可将式（1）改写成

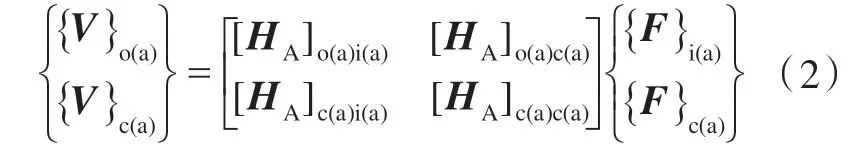
式中：{V }o(a)和{V }c(a)为振动响应{VA} 的子向量；{F }i(a)和{F}c(a)为外部激励矩阵{FA} 的子向量。

同样地，对于另一个与子结构A 耦合的子结构B，可以得到

或

1.2 多子结构耦合

当把子结构A 和子结构B 作为一个耦合系统来考虑时，耦合系统的矩阵式可以写成如下形式：

或

式中，{Vs}，[Hs]和{Fs} 分别为系统坐标下的响应、传递矩阵和激励矩阵。

图2 所示的双子结构由n 个柔性耦合系统连接，其中Rc和Xc分别为耦合点的力与位移。

图2 柔性耦合系统示意图Fig.2 The sketch of flexibility coupling system

针对每个子结构单独进行分析，可以得到

其中，

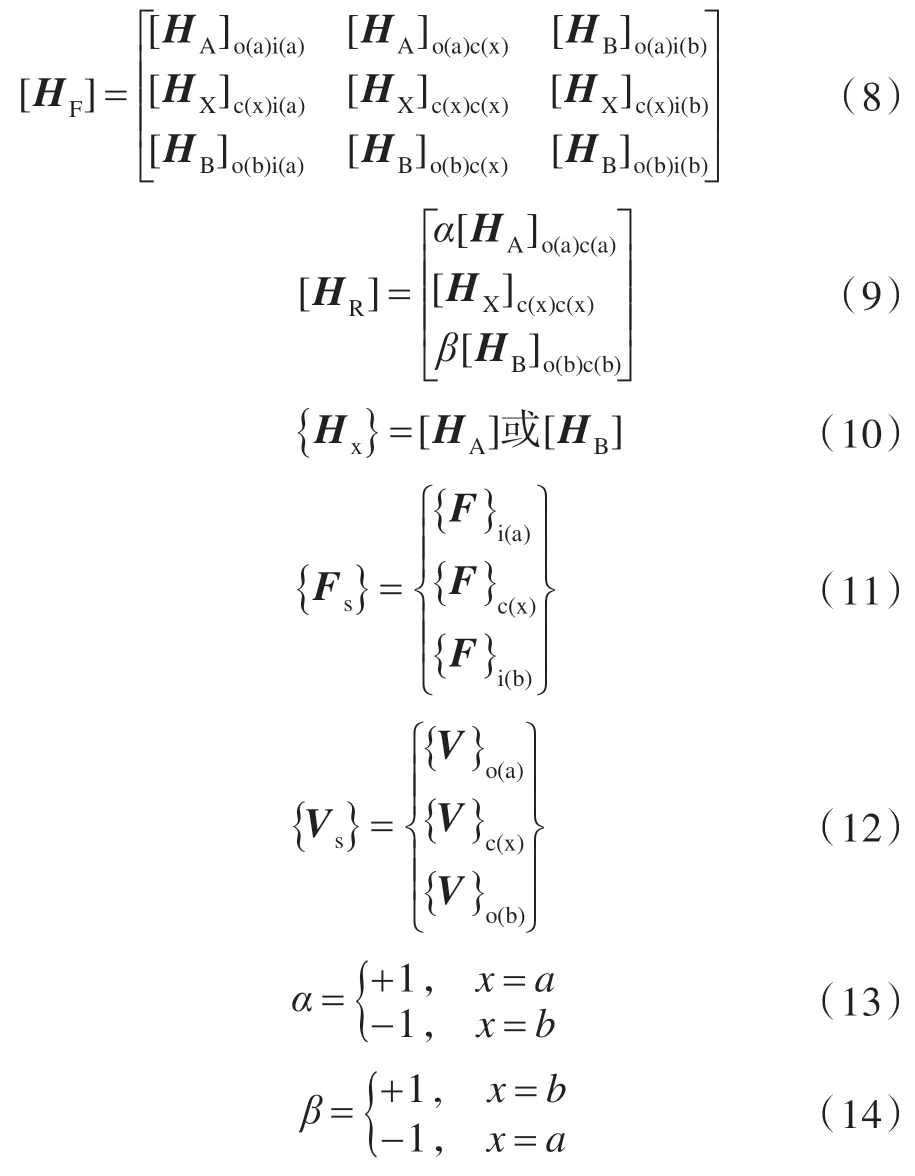
若将隔振器视为无质量的弹性阻尼元件，利用力平衡以及速度连续性条件，力的大小相等，方向相反，隔振器为线性弹簧，满足胡克定理，即

式中，[Ks]为柔性耦合刚度矩阵，对应于x，y，z 方向的位移自由度。在工程中，一般情况下各个柔性耦合子系统x，y，z 方向上的互耦合相对较弱，基本可以忽略，则[Ks]可表示为

其中，对角线上的非零子矩阵为

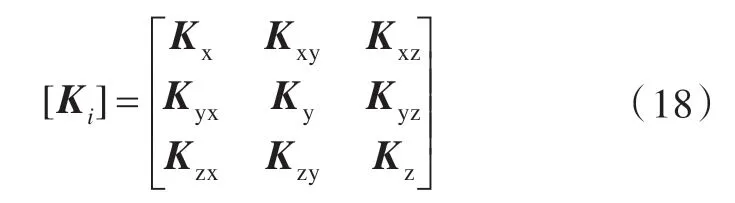
根据矩阵（6）的第2 行和第3 行，可得

将式（17）和（18）代入式（16），可得

其中，

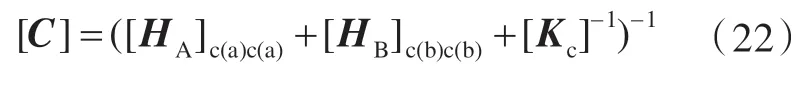
将式（21）代入到式（7），并对比式（6），可以推出耦合系统的传递函数矩阵与子结构A，B 的传递函数矩阵的关系如下：

如果仅在子结构B 上作用有一组激励力Fi(b)，则在子结构A 上的响应可表达为

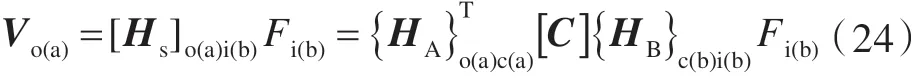
2 FBS 理论的改进

从上文可以看出，对于柔性耦合系统，现有的FBS 理论将隔振器视为无质量的弹性阻尼元件，该假设在低频段通常误差较小，但在中、高频段，由于隔振器的质量效应占主导，故计算误差将会越来越明显。

而基于四端参数的隔振器阻抗矩阵能精确表征隔振器的动态特性，可以有效消除上述误差，且目前中、高频段隔振器阻抗矩阵测量已相对成熟。

对于图2 所示的柔性耦合系统，基于隔振器阻抗矩阵，利用力平衡以及速度连续性条件，式（15）和式（16）变为（仅考虑子结构B 上作用有一组激励力Fi(b)）：

将式（25）代入式（27），

将式（25）和式（30）代入式（28），

将式（25）、式（30）和式（31）代入式（26），可得

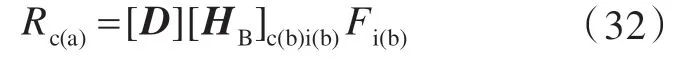
其中，

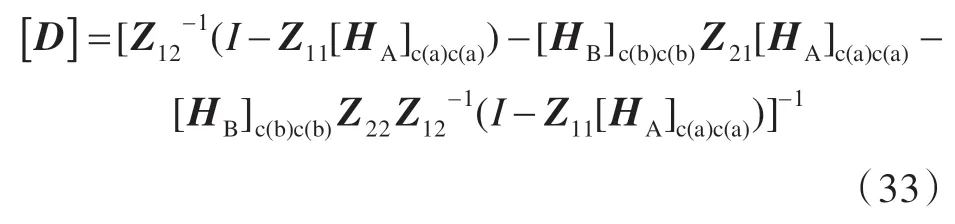
同样地，将式（32）代入到式（7），并对比式（6），如果仅在子结构B 上作用有一组激励力Fi(b)，则在子结构A 上的响应可表达为

3 改进效果对比

针对试验室某浮筏系统模型，筏架尺寸为1 500 mm ×700 mm ×100 mm，隔振器为6 个BE40型橡胶隔振器，采用2 个激振器激励，模拟实船对隔振系统的评价考核，激励点选在浮筏上层设备安装位置，响应点选为基座，如图3 所示。激振力为白噪声，频率范围为10～2 000 Hz，激励力满足性噪比要求。计算中，隔振器阻抗矩阵参数来自测试数据，浮筏结构及基座结构的阻抗矩阵通过有限元建模仿真计算得到。在中、高频段，有限元仿真计算的主要误差来自边界约束条件的等效，而上述结构的阻抗矩阵为其无约束自由状态下的频响，因此计算精度满足工程要求。图4 所示为激励点到隔振器上端筏架连接点的频响函数计算值与测试值的对比（参考值为1×10-6m/（s2·N-1））。

将现有的FBS 方法基座振动加速度级响应计算结果以及改进后的FBS 方法计算结果与测试结果进行了对比，分别如图5 和图6 所示。从图中可以看出，在中、高频段，改进后的FBS 方法的精度有了明显提高，总误差也由之前的约6 dB提升到3 dB 以内。

图3 浮筏隔振系统模型试验Fig.3 The testing model of the floating raft isolation system

图4 浮筏结构频响计算结果与测试结果对比Fig.4 The comparison between the testing and calculated result of the floating raft structure FRF

图5 现有FBS 方法计算结果与测试结果对比Fig.5 The comparison between the testing result and the result calculated by the existing FBS method

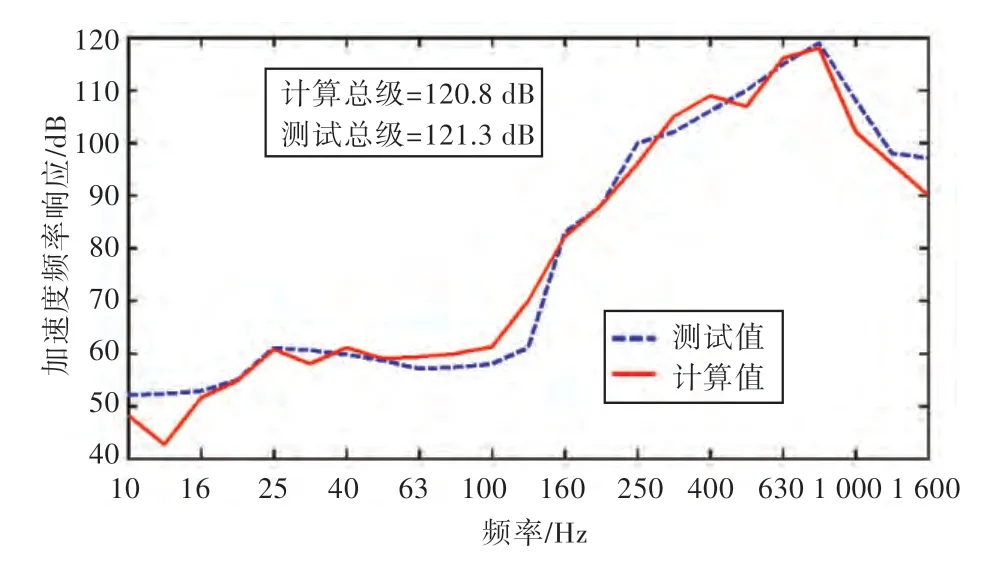
图6 改进后的FBS 方法计算结果与测试结果对比Fig.6 The comparison between the testing result and the result calculated by the improved FBS method

4 结 语

本文根据浮筏隔振系统的特点，针对现有FBS 方法的不足，推导了基于隔振器阻抗矩阵的浮筏隔振系统动态特性计算公式，从理论上消除了隔振器特性模拟所带来的误差。实验室模型试验表明，相对于现有的FBS 方法，改进后的计算方法精度更高。

［1］姚耀中，林立.潜艇机械噪声控制技术综述［J］.舰船科学技术，2007，29（1）：21-26.YAO Yaozhong，LIN Li.A review of control of mechani⁃cal noise for submarines［J］.Ship Science and Technol⁃ogy，2007，29（1）：21-26.

［2］马永涛，周炎.舰船浮筏隔振技术综述［J］.舰船科学技术，2008，30（4）：22-26.MA Yongtao，ZHOU Yan. Summary of floating raft sys⁃tem［J］. Ship Science and Technology，2008，30（4）：22-26.

［3］高云剑，黄修长，华宏星.基于频响函数综合的浮筏隔振系统误差传递分析［J］.噪声与振动控制，2013，33（3）：39-43.GAO Yunjian，HUANG Xiuchang，HUA Hongxing.Analysis of uncertainty propagation in floating raft sys⁃tem using FRF-based substructuring method［J］.Noise and Vibration Control，2013，33（3）：39-43.

［4］吴震东，华宏星.基于频响函数合成的浮筏隔振系统的响应研究［J］.噪声与振动控制，2007，10（5）：24-27.WU Zhendong，HUA Hongxing. Research of the raft system based oil frequency response funcfion coupled method［J］.Noise and Vibration Control，2007，10（5）：24-27.

［5］尚国清，邱伯华.浮筏装置系统的动力学特性分析［J］.舰船科学技术，2000，6（1）：11-15.SHANG Guoqing，QIU Bohua.The dynamic characteris⁃tic of raft system.［J］Ship Science and Technology，2000，6（1）：11-15.

［6］吴广明，余永丰，沈荣瀛，等.模态机械阻抗综合法及其在隔振系统中的应用［J］.噪声与振动控制，2003，23（2）：13-16.WU Guangming，YU Yongfeng，SHEN Rongying，et al.Modal mechanical impedance synthesis method and its application in isolation system［J］. Noise and Vibration Control，2003，23（2）：13-16.

［7］鲁克明，叶珍霞，赵应龙.基于有限元法的船用浮筏隔振系统仿真计算［J］.武汉理工大学学报，2006，30（5）：86-88.LU Keming，YE Zhenxia，ZHAO Yinglong. Simulating calculation of onboard floating raft system based on fi⁃nite element method［J］.Journal of Wuhan University of Technology，2006，30（5）：86-88.

［8］彭伟才，刘彦，原春晖.浮筏隔振系统有限元模型中基座的等效方法［J］.中国舰船研究，2012，7（3）：89-92.PENG Weicai，LIU Yan，YUAN Chunhui.Equivalent machinery base method for finite element analysis of floating raft isolation system［J］. Chinese Journal of Ship Research，2012，7（3）：89-92.

［9］黄修长，徐时吟，张志谊，等.基于频响函数综合的舱筏隔振系统灵敏度分析和优化［J］.振动与冲击，2011，30（5）：145-151.HUANG Xiuchang，XU Shiyin，ZHANG Zhiyi，et al.Design sensitivity analysis and optimization of a float⁃ing raft system using a FRF-based substructuring method［J］. Journal of Vibration and Shock，2011，30（5）：145-151.

［10］LIU L. A frequency response function-based inverse substructuring approach for analyzing vehicle system NVH response［D］.Alamaba：The University of Ala⁃bama，2002.