AKNS方程的三线性型及周期孤立波解
2022-08-18傅海明戴正德
傅海明, 戴正德
(1.广州华夏职业学院 教育学院, 广州 510935; 2.云南大学 数学与统计学院, 昆明 650091)
求解非线性波方程是一项很难而且很重要的研究,从而吸引了一大批勇于挑战、不懈努力的学者寻找求解的方法.现有的主要方法有逆散射法[1], Backlund法[2], Darboux变换法[3], Hirota双线性法[4-6], F-展开法[7-8],齐次平衡法[9], Jacobi椭圆函数展开法[10],包络变换法[11-12],ADM方法[13]和指数函数法[14]及双指数函数法等.这些方法还不足以求解所有波方程,所以不少科学家们还在不断深入研究当中.
Hirota方法已经研究较为成熟,三线性型的求解更为困难,本文借助新试探函数,利用数学软件 Matlab,求解了Ablowitz-Kaup-Newell-Segur方程
4uxt+uxxxy+8uxyux+4uyuxx=0
(1)
获得了若干其他方法不曾给出的形式更为丰富的新的显式周期孤立波解.不难看到该方法还是很高效的,也可以看出该方法适用于相当一部分非线性方程.
1 Ablowitz-Kaup-Newell-Segur方程的三线性型
关于Ablowitz-Kaup-Newell-Segur方程,引入如下形式变换
u=(lnf)x
(2)
将式(2)代入方程(1),并整理化简化为如下三线性型形式:
(3)
2 Ablowitz-Kaup-Newell-Segur方程的三线性型
假设方程(3)有如下形式的解:
f(x,y,t)=e-ξ+aeξ+bcosη
(ξ=kx+hy+wt,η=px+qy+γt)
(4)
将式(4)代入方程(3),得到一个关于 的多项式,令其系数全为得到如下代数方程组:
ak2(w+4k2h)=0
(5)
b(-k2γ-2kwp-k4q-4k3hp+4p3kh+6p2qk2+p2γ-p4q)=0,
(6)
b(-4k3pq+k2w-p2w-2kpγ+k4h+p4h+4kp3q-6k2hp2)=0,
(7)
b2(-4khp3-p2γ+k2γ+2kpw+hp4+k4q+4k3hp-6k2hp2)=0,
(8)
2b2(-2kpγ-k2w-p2w-2k3pq+6kp3q+2hp4-2k2hp2)=0,
(9)
b2(-k2w-p2w-2kpγ-k4h+3hp4+8kp3q+2k2hp2)=0,
(10)
2ab(3k2γ+p2γ+6kpw-p2q+7k4q+20k3hp-4khp3-42k2p2q)-2b3p2(γ-4p2q)=0,
(11)
ab2(-4khp3-p2γ+k2γ+2kpw+p4q+k4q+4k3hp-6k2p2q)=0,
(12)
ab2(k2w+p2w+2kpγ+k4h-3p4h-8kp3q-2k2hp2)=0,
(13)
2ab2(2kpγ+p2w+2k3pq-6kp2q-2hp4+2k2hp2)=0,
(14)
a2b(4k3pq-k4h-k2w+2pγ-p4h-4kp3q+6k2hp2)=0,
(15)
a2b(p2γ-k2γ-2kpw-p4q-k4q-4k3hp+4khp3+6k2p2q)=0.
(16)
利用数学软件Matlab解以上方程组,得到以下几种情况:
情形I:
b=0,p=0,q=0,γ=0,
a=a,k=k,h=h,w=-4k2h.
(17)
将式(17)代入式(4)得
f(x,y,t)=aeξ+e-ξ.
(18)
1) 如果a>0,则式(18)变为
(19)
将式(19)代入式(2)得到Ablowitz-Kaup-Newell-Segur方程的解为
(20)
其中:a>0,h,k为任意常数.
2) 如果a<0,则式(18)变为
(21)
将式(21)代入式(2)得Ablowitz-Kaup-Newell-Segur方程的解为
(22)
其中:a<0,h,k为任意常数.
3) 如果a=0,则式(18)变为
f(x,y,t)=e-ξ.
(23)
将式(23)代入式(2)得Ablowitz-Kaup-Newell-Segur方程的解为
u3=-k.
(24)
其中:k为任意常数.
情形II:
a=0,h=0,p=0,w=0,
b=b,k=k,q=q,γ=-k2q.
(25)
将式(25)代入式(4)得
f(x,y,t)=e-ξ+bcosη.
(26)
将式(26)代入式(2)得Ablowitz-Kaup-Newell-Segur方程的解为
(27)
其中:b,k,q为任意常数.
情形III:

(28)
将式(28)代入式(4)得
f(x,y,t)=aeξ+e-ξ+bcosη.
(29)
1) 如果a>0,则式(29)变为
(30)
将式(30)代入式(2)得Ablowitz-Kaup-Newell-Segur方程的周期孤立波解为
(31)
其中:a>0,b,k,h,p为任意常数.
从图1~4可以看出,只改变参数的值时,孤立波的周期明显改变了,而且周期越小时波峰越平缓.

图1 当a=1,b=2,k=1.1,h=-2,p=0.5,t=0时,u5的图像

图2 当a=1,b=2,k=1.1,h=-1,
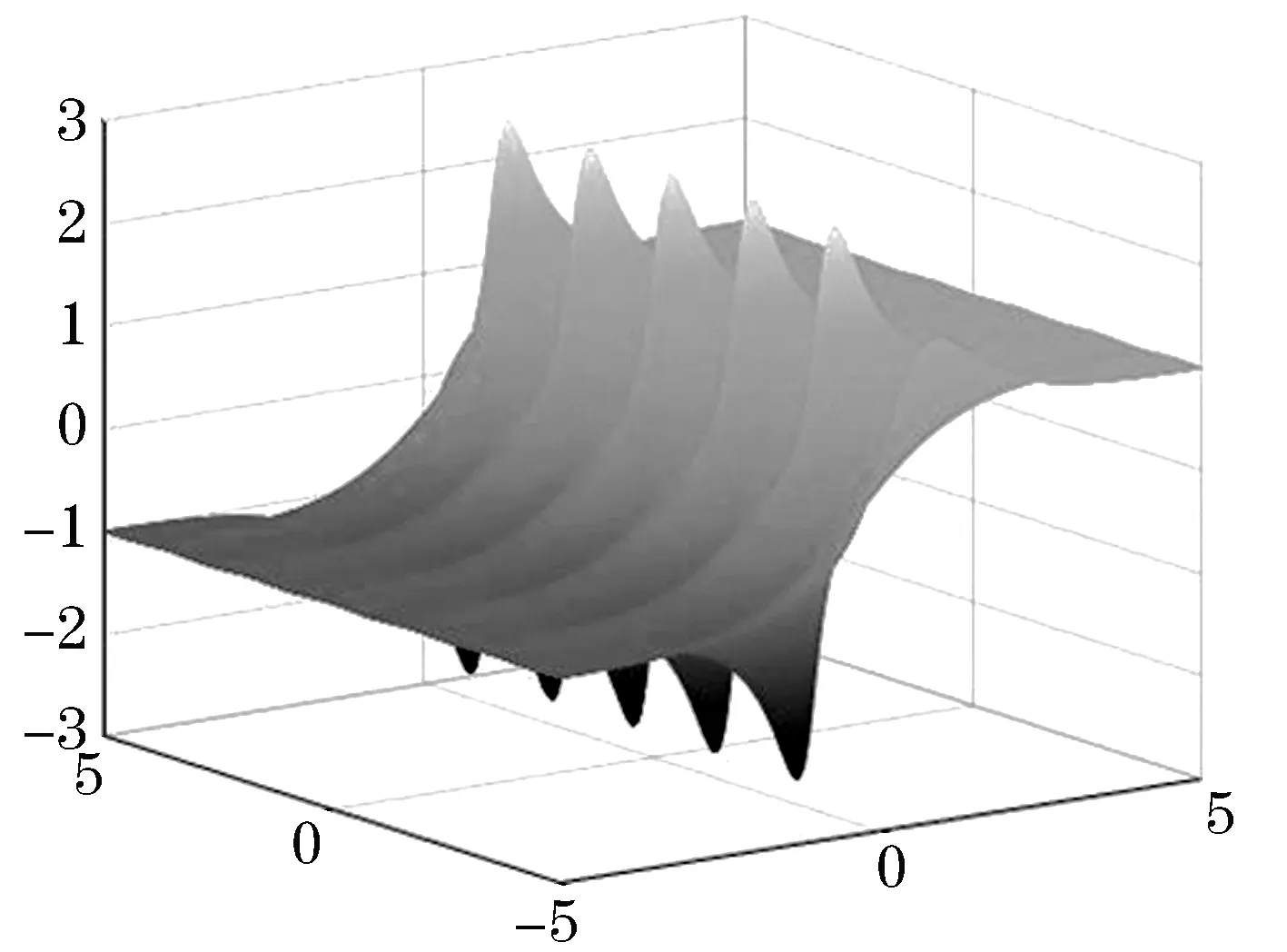
图3 当a=1,b=2,k=1.1,h=0,

图4 当a=1,b=2,k=1.1,h=1,
只改变参数k的值作出图5~10,可以看出,当k<1时,u5在原点附件形成爆破圈;当k<1越接近时,爆破圈的半径越小;当k=1时,u5在原点爆破;当k>1时,u5在原点附近是连续的.

图5 当a=1,b=2,k=0.8,h=5,

图6 当a=1,b=2,k=0.9,h=5,

图7 当a=1,b=2,k=0.99,h=5,

图8 当a=1,b=2,k=1,h=5,

图9 当a=1,b=2,k=1.001,h=5,

图10 当a=1,b=2,k=1.01,h=5,
2) 如果a<0则式(29)变为
(32)
将式(32)代入式(2)得Ablowitz-Kaup-Newell-Segur方程的周期孤立波解为
(33)
其中:a<0,b,k,h,p为任意常数.
3) 如果则式(29)变为
f(x,y,t)=e-ξ+bcosη.
(34)
将式(34)代入式(2)得Ablowitz-Kaup-Newell-Segur方程的解为
(35)
其中:b,k,h,p为任意常数.
3 结 语
本文研究了三线性型的求解方法,用新的测试函数来尝试求解.以Ablowitz-Kaup- Newell-Segur方程为例,给出该方法求孤立波解和周期孤波解的具体过程,得出新的孤立波解和周期孤波解,并以此讨论了该方程的周期性和爆破性.
