基于部分观测识别非线性高层剪切框架结构参数与未知地震作用

2023-01-03戚铖恺吴嘉敏黄金山

振动与冲击 2022年24期

戚铖恺，吴嘉敏，黄金山，杨宁

(1. 厦门大学建筑与土木工程学院，福建厦门 361005； 2. 厦门大学航空航天学院，福建厦门 361005；3. 科廷大学土木与机械工程学院，澳大利亚珀斯 6102)

实时掌握结构状态信息和地震激励信息是进行结构抗震安全评估和优化振动控制的前提[1-8]。地震信息通常可以从地震台网或安装在结构上的健康监测(structure health monitoring，SHM)系统获取[9]，但是传播介质可能影响监测系统的测量精度[10]，而且并非所有被监测的结构都安装了测量基底激励的加速度计。过去已有很多学者提出了利用结构响应的实测值反演未知激励的方法[11-15]，但这些方法多适用于非地震荷载的识别。这是因为结构在地震作用下的运动方程为相对于地面坐标系下的相对运动方程，现行方法的实现依赖于结构相对响应的观测值[16-19]，而SHM系统测得的是结构的绝对响应，在未知地震动下无法直接转换为相对于地面的响应，给地震激励的识别带来困难。因此，基于绝对坐标系下建立运动方程的识别方法受到关注。Zhao等[20-21]在绝对坐标系下建立运动方程，利用所有自由度的全部响应观测值同时识别结构参数和未知地面荷载。但随着现代结构日益大型化和复杂化，获取全部响应信息是不现实的。Li等[22-23]结合模态方法，在绝对坐标系中建立动力学方程以避免将绝对加速度观测值转换为相对模态加速度的困难，但仅限用于结构参数已知的情况下进行未知地面激励的识别。此外，此类在绝对坐标系下建立运动方程的识别方法往往需要建立近似假设，故只适用于剪切型建筑的识别。最近，Huang等[24]和Lei等[25]提出了未知激励下的卡尔曼滤波(generalized Kalman filter with unknown input，GKF-UI)方法和未知激励下的扩展卡尔曼滤波(generalized extended Kalman filter with unknown input，GEKF-UI)方法。这些方法在相对坐标系下建立运动方程，观测量为部分自由度的绝对加速度，有效地实现了结构参数与未知地面激励的同时在线识别，且克服了需要建立近似假设的问题。但是，GEKF-UI基于传统扩展卡尔曼滤波(extended Kalman filter，EKF)方法的框架推导，需要每一时间步都计算雅可比矩阵，当结构自由度增多时，会增加识别困难，甚至无法得到识别结果，因此不适用于自由度较多的结构，尤其是未知地震激励下的高层建筑识别。

地震作用下采用部分观测结构响应对高层建筑进行识别一直是许多学者研究的重点。高层建筑因其多自由度的特点，往往存在计算过程复杂，识别误差易累积等问题。当地震激励较强时，高层建筑结构将出现非线性变形，现有的模态展开方法将难以适用。子结构方法的“分而治之”思想给高层建筑的识别提供了另一种思路。Koh等[26]将大型结构划分为若干子结构，提出了基于EKF的子结构识别方法，但需要观测子结构界面上所有加速度、速度及位移响应。另外，Koh等[27]改进了该方法，同样将大型结构划分为若干子结构，仅采用部分加速度观测值实现未知激励下大型结构的识别，但该法同样需要子结构边界处的加速度响应观测值。国内外一些研究者亦将子结构方法运用到非线性工况中，Kumar等[28]运用遗传算法与神经网络滤波算法的结合算法，观测子结构的边界响应识别结构参数及非线性阻尼系数。陶冬旺等[29]将整体结构划分为线性子结构和非线性子结构，通过EKF和无迹卡尔曼滤波进行识别。Al-Hussein等[30]先选取一个子结构运用未知激励下的最小二乘法进行识别，然后利用已被识别的子结构信息识别整体结构，该法也难以避免误差累积。

作者所在的课题组也已针对高层建筑结构系统识别和未知地面激励识别做了一些研究。在结构参数已知方面：Huang等提出了在绝对坐标系下建立运动方程，结合模态展开的方法识别未知地面激励；Huang等还提出了GKF-UI方法，实现了在相对坐标系下建立运动方程，基于绝对加速度响应量识别未知地面激励。在结构参数未知方面：文献[31]中提出了将模态展开与GEKF-UI相结合的方法，降低了识别过程中结构状态的维度且不增加未知地面激励的维度，避免了误差累积的问题，从而提高了高层建筑结构系统识别的效率与精度，但该法仅适用于线性工况；文献[32-34]的基本思想是将EKF和子结构方法相结合，文献[32]中基于部分观测信息实现对未知地面激励下线性高层建筑结构的识别，文献[33]中将方法推广到结构损伤识别的应用中，文献[34]中考虑高层建筑结构在非线性工况下的识别，虽然上述方法识别结果都较好，但是存在相邻子结构之间状态识别信息传递的情况，造成识别误差累积。

本文的目的在于进一步将子结构方法运用到非线性高层剪切框架结构的状态、参数与未知地震作用的识别上，克服目前大多数方法仍存在需要子结构边界处观测信息、无法独立并行识别、存在累积误差等不足。为此，本文在对整体结构划分后，把相邻子结构之间的作用视为子结构的附加未知激励，并根据受力情况将地震作用下的剪切框架子结构进行分类分析，各子结构基于内部的部分观测量运用GEKF-UI方法识别子结构的状态、参数和未知激励。通过一个12层的非线性剪切框架来验证该方法的有效性。

1 方法提出

1.1 子结构在相对坐标系下的运动方程

地震作用下n自由度非线性结构的运动方程可写为

(1)

第一类子结构(图1 Sub.1)

(2)

式中：下标“u”为未知；下标“S”为子结构，其包含的自由度为s(s≤n)；IS为s×1的单位向量；fS,u，ηS,u分别为未知激励矩阵(np×nt)和未知激励定位矩阵(s×np)，其中np为未知激励数，nt为采样时间维度；fSB为未知边界力，其大小等于该子结构上部楼层的层间力，相应于图1 Sub.1，则有fSB=fq+1，其余子结构类似；ηSB为未知边界力定位矩阵。

第二类子结构(图1 Sub.2～Sub.m-1)

(3)

第三类子结构(图1 Sub.m)

(4)

图1 子结构划分示意图Fig.1 Substructure division

1.2 子结构状态方程的建立

(5)

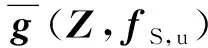
(6)

其中

(7)

(8)

在对未知激励进行线性化时，采用了Ding等提出的一阶保持假定,则将状态方程线性化和离散化后可表示为

Zk+1=AkZk+BkfS,u,k+Bk+1fS,u,k+1+gk |k+wk

(9)

式中：Ak=eGk | kΔt，Δt为采样间隔；wk为均值为0，方差为Q的模型误差。

gk |k=(Ak-IS)(Gk |kΔt)-1·

(10)

(11)

1.3 子结构观测方程的建立

三类子结构因受力情况有差异，其观测方程的表达方式亦有区别。

(1) 第三类子结构只在底部受到激励，只需观测子结构中的部分绝对加速度，观测方程可表示为。

(12)

(2) 第一类和第二类子结构不仅受到地震激励，还在边界处有上部子结构对其产生的边界作用力，因此在识别这两类子结构时，观测方程中除绝对加速度外，还需融合部分层间位移数据防止识别结果的漂移，于是观测方程可写为

(13)

将式(12)观测方程线性化后可表示为

(14)

式中：vk+1为均值0,方差为R的观测误差

(15)

由于本文观测的是绝对加速度响应，且不观测子结构边界处响应，所以Dk+1 |k实际上是一个零矩阵，即输入与输出之间无直接馈通。

1.4 基于GEKF-UI的识别过程

限于篇幅，本文简要给出GEKF-UI方法的主要公式，详细的推导过程可参考Lei等的研究。

首先进行结构状态估计

(16)

(17)

(18)

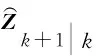
(19)

然后对误差运用加权最小二乘求解未知激励

(20)

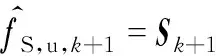
(21)

其中

(22)

(23)

误差矩阵计算如下

(24)

(25)

(26)

误差协方差矩阵计算结果如下

(27)

(28)

(29)

(30)

(31)

传统的剪切型子结构识别过程中往往会将某一子结构已识别得到的结果用于下一子结构的识别中，上一子结构已识别得到的结果与真实值之间的误差就会传递给下一子结构，从而出现误差累积。子结构与GEKF-UI相结合的方法将子结构间的相互作用作为子结构的附加未知激励识别，也即各子结构成为独立的待识别体，识别结果互不传递，可实现子结构的并行识别，避免识别误差的累积。

2 数值算例与分析

高层结构变形模式受高宽比控制，高宽比较小的框架结构(H/B≤3)的变形模式以剪切变形为主，本文的算例模型是基于高宽比较小的剪切型框架。为验证提出的方法识别非线性剪切框架结构的有效性，设计了一12层剪切框架，每层质量，刚度及阻尼参数分别为mi=3.2×105kg，ki=2.5×108N/m，ci=5.2×105N·s/m,i=1, 2,…,12。该结构受到El-Centro地震波的N-S分量激励，地面峰值加速度为0.3g。本算例的地震激励幅值较强，极有可能在底层产生非线性变形。假设第i层非线性滞回分量zi符合Bouc-Wen模型

(32)

(33)

αi为结构第i层柱屈服后与屈服前刚度之比；在本算例中，结构非线性参数取值：βi=4 000 m-2，γi=2 000 m-2，ni=2，αi=0.1(i=1,…,4)。

将该12层剪切框架划分为两个独立的子结构，第1层～第6层为子结构1，属于第一类子结构；第7层～第12层为子结构2，属于第三类子结构。子结构的识别流程图，如图2所示。

图2 子结构识别流程图Fig.2 Flow chart of substructure identification

2.1 子结构1

在识别子结构1时，非线性层的位置未知，假设每层都发生非线性变形，通过识别的非线性模型参数大小判断是否发生非线性。该子结构受到未知地震激励和未知边界力。仅观测第1、第3、第5层的绝对加速度和第1、第2、第4层的层间位移，所有观测数据均加上2%均方根(root mean square,RMS)水平的噪声。地震激励识别图，如图3(a)所示。为了更清晰展示识别值与理论值的对比，图中仅列出了前15 s的地震激励时程，总体符合程度较高。边界力识别图，如图3(b)所示。其识别效果要好于地震激励，可以看到，识别值与真实值高度吻合。结构的第4层位移、第6层速度和第1层恢复力滞回曲线识别图，分别如图3(c)～图3(e)所示。识别结果均很好。

图3 未知地震作用和边界力作用下子结构1识别结果Fig.3 Identification of the substructure 1 under unknown seismic excitation and unknown boundary force

第3层刚度识别，如图4(a)所示。识别值能快速收敛且误差小。第3层阻尼系数识别，如图4(b)所示。识别值误差较小，但收敛速度比刚度识别慢。非线性参数的识别图，如图5所示，其收敛速度较快，其中γ的识别误差比β大，但仍在可接受范围内。

图4 第3层刚度和第3层阻尼系数识别对比Fig.4 Comparison of the identified stiffness and damping coefficient of the 3rd floor

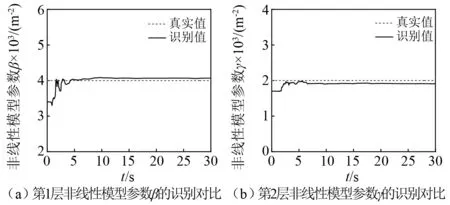
图5 非线性模型参数β和γ的识别对比Fig.5 Comparison of the identified non-linear modal parameters β and γ

子结构1所有楼层的刚度、阻尼系数和非线性参数的识别情况，如表1所示。刚度识别误差不超过2%，阻尼系数识别误差基本在3%以内；第5层和第6层的非线性参数识别值近似为0，表明只有第1～第4层发生了非线性变形。

表1 子结构1刚度、阻尼系数及非线性参数识别情况Tab.1 Comparison of identified structural stiffness, damping coefficients and non-linear parameters of the substructure 1

2.2 子结构2

在地震作用下，剪切框架结构下部的剪切变形大于上部，较容易进入非线性。由子结构1的识别结果可知，非线性行为发生于底层1～4层，第5、第6层仍处于线性状态，所以剪切框架的7～12层也为线性体，因此将子结构2作为线性结构识别，但本文提出的方法也同样适用于结构下部和上部均发生非线性的情况。

根据式(4)，该子结构只受到在底部输入的第6层绝对加速度引起的未知激励。仅观测第7、第8、第11层的绝对加速度，所有观测数据均加上2%RMS水平的噪声。可以看到，图6中的未知激励以及结构第9层与第8层的层间位移、第12层与第11层的层间速度识别值与真实值均符合好。

图6 子结构2识别结果Fig.6 Identification results of the substructure 2

第8层和第12层刚度识别图，分别如图7(a)、图7(b)所示，两者识别误差均很小且收敛速度很快。

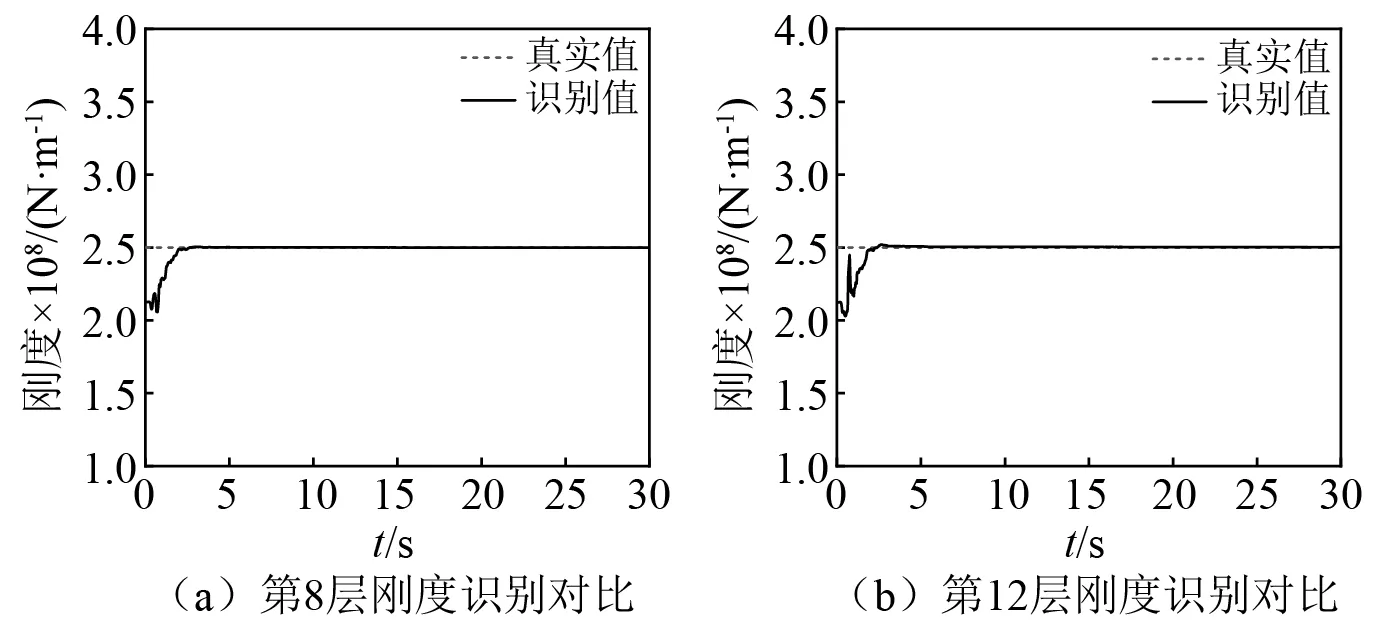
图7 第8层和第12层刚度的识别对比Fig.7 Comparison of the identified stiffness of the 8th and 12th floors

第9层和第10层阻尼系数的识别图，分别如图8(a)、图8(b)所示，收敛速度较快，识别误差分别为-2.03%和2.23%。

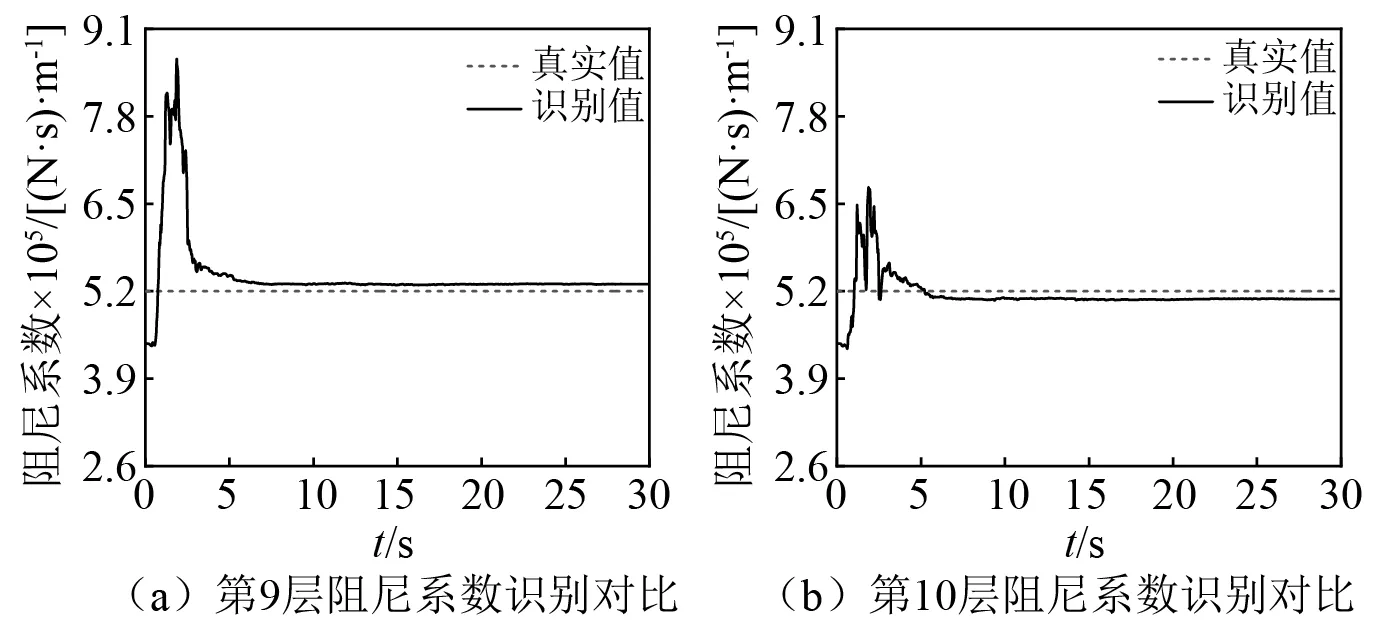
图8 第9层和第10层阻尼系数的识别对比Fig.8 Comparison of the identified damping coefficients of the 9th and 10th floors

子结构2所有楼层的刚度和阻尼系数识别情况，如表2所示。刚度识别误差均在3%以内，阻尼系数识别误差均在7%以内，总体而言，刚度的识别误差要小于阻尼系数。

表2 子结构2刚度和阻尼系数识别情况Tab.2 Comparison of identified structural stiffness and damping coefficients of the substructure 2

由算例结果可知，在仅观测部分绝对响应的条件下，无需其他子结构和边界处的观测信息，可以独立地识别每个子结构的参数、状态及输入，证明提出的子结构与GEKF-UI相结合的方法可有效应用于未知激励及高层非线性结构的识别中。此外，本文采用的观测数据在进行识别时没有进行前处理，而是直接输入所提方法框架中，由此可见所包含的噪声水平已经能很好地验证所提方法的鲁棒性。