FPSO液舱晃荡与船舶时域耦合运动数值模拟

操戈，李旭，张咏鸥，王康

1 海军装备部 驻武汉地区军事代表局，湖北武汉430064

2 华中科技大学船舶与海洋工程学院，湖北武汉430074

3 华中科技大学船舶与海洋工程水动力学湖北省重点实验室，湖北武汉430074

0 引 言

随 着LNG（Liquefied Natural Gas），FPSO（Floating Production Storage and Offloading）和FLNG（Floating Liquefied Natural Gas）等液货船的发展，液舱晃荡对船舶运动的影响成为关注的热点。此外，为满足市场需求，船舶尺寸越来越大，船舶运动与液舱晃荡的耦合影响也愈发重要。

与船舶耦合的液舱晃荡在过去的研究中被简化为自由液面或者质点弹簧，这能精确求解小幅晃荡。几十年来，人们针对耦合运动进行了许多研究，主要分为2 类：基于线性势流理论的频域研究和基于非线性粘性流的时域研究。Molin 等［1］基于线性势流理论的频域方法研究了船舶与液舱晃荡的耦合运动，研究假设船舶液舱的运动是线性的，但当液舱晃荡很激烈时，线性理论就有一定的局限性。船舶与液舱晃荡的时域耦合运动是最近研究的热点问题，脉冲响应法（Impulse Response Function，IRF）被用于求解时域耦合问题。Cummins［2］利 用IRF法将船舶频域结果转化为时域结果进行了分析。Kim 等［3］将IRF 法扩展到求解船舶与液舱晃荡耦合运动，并验证得到仿真计算结果与试验结果具有较好的一致性。李裕龙等［4］基于OpenFOAM 研究了船舶与液舱晃荡在波浪中的时域耦合运动，数值模拟计算能够清晰地显现出液舱晃荡对船体全局运动的影响，且船体运动计算结果与模型试验结果吻合良好。洪亮等［5］对S175 加载方形液舱在迎浪、横浪等不同工况下液舱流体晃荡及其与船体运动时域耦合分别进行了计算模拟与验证研究，耦合运动模拟结果能清晰地反映液舱晃荡对船体运动的影响，且数值结果与试验结果吻合良好，并具有较高的计算效率。黄硕等［6］对LNG 船和FPSO 液舱晃荡与船舶耦合运动问题的研究思路及进展进行了综述，分别对求解该类问题的模型试验和数值计算方法的最新研究成果进行了总结，分析了模型试验的特点和数值计算方法的应用范围，探讨了试验研究与数值模拟的关键技术及优缺点，并提出了加强相关研究的建议。

试验是研究船舶与液舱晃荡耦合运动最有用的方法之一。模型试验结果常用于证实理论和仿真计算结果的准确性。为研究液舱晃荡对船舶运动的影响，Molin，Clauss 以及李裕龙等［1，4，7］进行了一系列的相关试验。

近年来，人们对由液舱晃荡引起的载荷也做了很多研究，提出了许多数值和理论的方法。Loots 等［8］提出了改进的VOF（Volume of Fluid）法以计算液舱晃荡的冲击载荷，并与试验数据进行了比较。Lee 等［9］利用CFD 软件计算了LNG 的矩形液舱在外部激励力作用下的响应，并和试验结果做了对比，研究表明液体粘性、液体与气体的压缩性，以及密度比对冲击载荷的影响很大。张书谊等［10］采用CFD 软件Fluent 模拟了二维矩形液舱在不同舱内水深、不同激振频率时的横荡，发现在距自由面较深点处，流体载荷的计算结果与试验值相符合。金晶等［11］根据改进的VOF 法建立了晃荡载荷计算方法，可用于对补给舰船的液舱晃荡设计载荷进行快速、准确的预报。但有关FPSO液舱晃荡与船舶耦合运动时域及频域计算方法的系统性分析还很少，液舱晃荡对船舶运动的影响在过去的研究中经常被忽略或线性化。因此，为准确预报FPSO 运动，本文拟计算不同液舱液量下液体粘性对液舱晃荡与船舶时域耦合运动的影响，并对时域及频域计算方法的适用性进行系统性分析。

本文将通过求解时域方程，采用能考虑液舱内流体粘性的CFD 软件Fluent 及IRF 方法分析船舶与液舱晃荡耦合运动，并将时域、频域方程求解结果与试验数据进行对比。一方面，通过CFD 计算液舱晃荡所产生的力及力矩，并以外力形式作用于船体；另一方面，将船舶运动仿真计算结果代入CFD 以求解液舱晃荡运动。通过两方面步骤的迭代计算，即可求解出船舶与液舱晃荡的耦合运动。随后，将试验结果与仿真结果进行对比以得到阻尼比的范围。最后，通过时域和频域方法求出不同液舱液量下船舶幅值响应算子（RAO）。

1 船舶与液舱晃荡耦合运动

1.1 船体运动与液舱晃荡固有频率

势流理论是计算船舶在诱导波中运动的有效方法。势流理论假设流体无粘无旋，那么速度势可用来表示整个流域，如式（1）所示：

式中，Φ 为流体速度势。由于船体表面的复杂性，直接求解整个流域的速度势较困难。速度势可以分解为入射势、绕射势和辐射势，可根据绕射理论和辐射理论分别予以求解。已知总的速度势就可求得到波作用于船舶的力。船体可视为刚性体，船体运动方程可写为

式中：M 为船体质量矩阵；C 为船体阻尼系数矩阵；K 为回复力刚度矩阵；Fw(t)为船舶受到的力；ζ 为船舶位移。

具有一定水深液舱的固有频率可以从波的色散关系中得出

式中：h 为水深；k 为波数；g 为重力加速度。液舱宽度和长度分别表征横向和纵向振型自由液面宽度，推导可得液舱每阶模态的固有频率

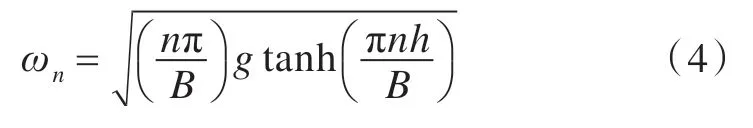
式中：ωn为第n 阶模态的固有频率；B 为液舱自由液面宽度；n 为频率阶次。

1.2 频域耦合运动

液舱晃荡会影响到船舶的运动，晃荡引起的力作为外部激励将作用于船体。受晃荡载荷作用的船舶6 个自由度的运动方程可写为

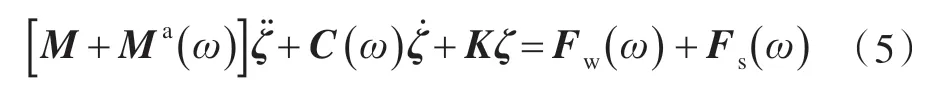
式中：Ma(ω)为船舶附加质量；Fs(ω)为液舱对船舶的作用力。质量矩阵M 包括液体的质量。忽略液舱内液体的惯性力，晃荡引起的载荷可写为

式中：Mas(ω)为液舱的附加质量；Cs(ω)为液舱的阻尼系数；Ks为液舱修正的回复力刚度，可以写为

式中：Is为液舱自由面对x 轴的二阶惯性矩；ρs为液舱内液体的密度。

横摇运动时粘性的作用不能忽略，可采取添加附加线性阻尼的办法来填补粘性的影响。

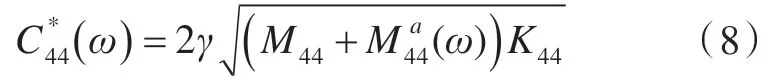
将式（6）和式（8）代入式（5），频域的耦合运动方程可改写为如下形式：

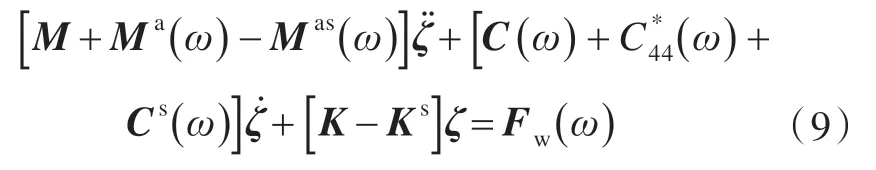
船舶运动位移和波浪力可以写成如下形式：

将式（10）代入式（9），可以得到频域耦合运动方程的另一种形式：

1.3 IRF 法

和附加质量、阻尼系数一样，所有的水动力系数均是在频域中求得，相应的力应转化到时域。利用IRF 法，经过推导，可得一阶波浪辐射力的表达式

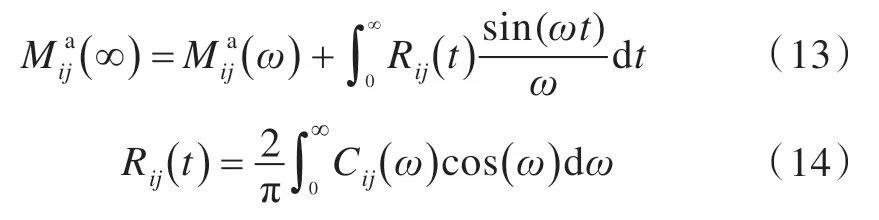
在实际的数值计算中，式（14）积分上限不可能是无穷大，存在数值计算截断误差，为减小这种截断误差，采用Kim 等［3］提出的方法，将改写为式（15）的形式，并对截断误差做相应的变换。

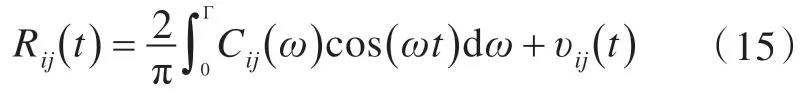
图1 给出了截止频率和截断误差对垂荡方向（Heave-Heave）迟滞方程数值的影响。图中：横坐标t 表示时间；纵坐标R33表示垂荡方向迟滞方程数值；ωmax为截止频率；L 为船舶长度。在时间较早时，迟滞方程的值较大，截断误差的影响较小，而到后期，截断误差的影响较大，可见有必要考虑截断误差的影响。

1.4 时域耦合运动

当考虑液舱对船舶运动影响时，船舶运动方程可写为

式中：Fext(t)表示波浪对船体表面的作用力；Fsa(t)表示液舱内液体晃荡引起的对液舱壁的作用力。将液舱内液体的惯性力从Fsa(t)分离出来，则Fsa(t)可改写为如下形式：

式中：Ms为液舱内液体的质量矩阵；为液舱内液体对液舱壁的静水力、水动力以及粘性力之和。

综合以上推导，船舶与液舱晃荡时域耦合运动方程可写为

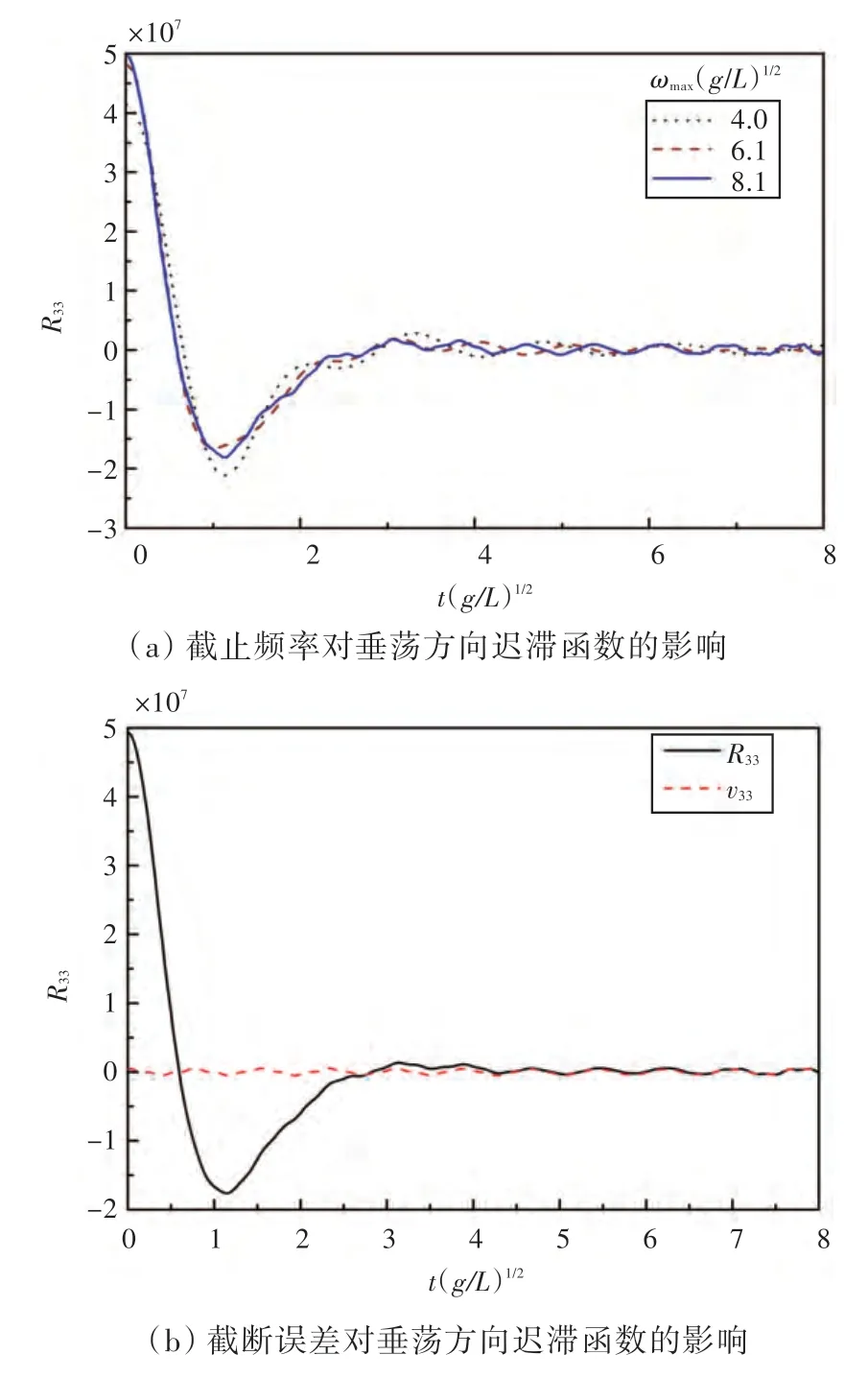
图1 截止频率和截断误差对垂荡方向迟滞函数的影响Fig.1 Effects of cut off frequency and truncation error on heave-heave retardation function

其中，

式中：Vliquid为液舱内液体体积；LGg为Gm与gs间的垂向距离，其中Gm为原始船舶的重力，gs为液舱内液体的重力。

2 计算方法及模型

2.1 数值计算方法

本文求解了船舶与液舱晃荡运动的频域方程和时域方程，求解这2 种方程涉及的程序以及相应的流程如图2 和图3 所示。

图2 船舶与液舱晃荡频域耦合运动计算流程图Fig.2 Flow chart of solving ship motion and tank sloshing coupling in frequency domain

图3 船舶与液舱晃荡时域耦合运动计算流程图Fig.3 Flow chart of solving ship motion and tank sloshing coupling in time domain

在频域中，利用法国船级社（BV）的三维水动力学软件Hydrostar 计算船舶以及液舱的水动力学系数（附加质量、阻尼系数等），通过求解船舶与液舱的频域耦合运动方程，得到船舶运动RAO。在时域中，利用Hydrostar 计算船舶的水动力系数以及波浪载荷，由IRF 法得到时域波浪辐射力。基于VOF 法，采用CFD 软件Fluent 模拟液舱晃荡，在Fluent 的UDF 中迭代求解船舶与液舱晃荡耦合运动的时域方程。数值求解得到的液舱晃荡力以及力矩作为外部激励作用于船体，船舶运动仿真计算结果逐步代入求解液舱晃荡运动。

2.2 FPSO 模型

引用MARINE 实验室完成的FPSO 试验作为算例求取船舶与液舱晃荡的耦合运动。图4 为船舶及液舱的几何外形。FPSO 的长、宽、吃水分别为285.0，63.0 和13.0 m，排水量为220 017.6 m3。图5 所示为FPSO 在Hydrostar 中的网格划分图，有5 024 个单元，图中液舱液量为56%。试验探讨了2 个液舱液量均为18%，37%和56%这3 种工况，后部液舱和前部液舱的长、宽、高分别为49.68，46.92，32.23 m 以及56.62，46.92，32.23 m，液舱底部至龙骨的距离为3.3 m。

图4 FPSO 外形与液舱分布图Fig.4 Sketch of FPSO with internal tanks

图5 FPSO 与液量为56%液舱网格划分图Fig.5 Mesh of FPSO and tanks（56% filling level）

3 结果及分析

3.1 固有频率及附加质量和阻尼系数

表1 给出了液舱液量为18%，37%和56%时横向与纵向振型的固有频率。除长度以外，2 个液舱的几何尺寸一样，因此，2 个液舱的横向固有频率相等，而结合式（4）可知，纵向固有频率不同。图6 和图7 分别为2 个液舱的横摇、纵摇附加质量和阻尼系数。图中横坐标ω表示频率，纵坐标分别表示横摇、纵摇附加质量和阻尼系数。

表1 液舱固有频率Tab.1 Natural frequencies of tanks

图6 前部液舱的横摇、纵摇附加质量和阻尼系数Fig.6 Roll and pitch added mass，damping coefficients of the front tank

图7 后部液舱的横摇、纵摇附加质量和阻尼系数Fig.7 Roll and pitch added mass，damping coefficients of the rear tank

3.2 阻尼比分析

横摇运动是最受关注的问题，当考虑液舱影响时，横摇运动变得更加复杂，求解式（11）可以得出船舶与液舱晃荡耦合运动幅值响应算子（RAO）。图8 给出了3 种液舱液量下船舶横摇运动RAO 试验值与频域计算结果的对比。图中：横坐标ω 表示频率；纵坐标表示横摇RAO；带圆圈的曲线表示MARINE 实验室完成的FPSO 试验结果。

图8 不同液量下横摇运动RAO 试验值与计算值对比（横浪）Fig.8 Comparison of roll RAO of experimental results and computational results at different filling levels（beam sea）

从图中可以看出，船舶液舱液量为0%时，一阶固有频率在0.5 rad/s 附近，但是一阶固有频率附近的计算结果和试验结果相比偏大，为了能使计算结果更加准确，加入了线性阻尼项，如式（8）所示。忽略液舱液量，系统阻尼比γ =0.1～0.15 时能够得到较好的频域结果。当液舱液量为18%时，液舱横摇一阶固有频率为0.49 rad/s，与船舶的一阶固有频率很接近，使得在0.42 rad/s 处RAO 波峰值变为波谷值，波峰值偏移到了0.6 rad/s 处。当液舱液量为37%和56%时，液舱的一阶固有频率分别为0.66 rad/s 和0.74 rad/s，远高于船舶的一阶固有频率，其第2 个峰值分别在0.76 rad/s 和0.8 rad/s 附近。随着液量的增加，第1 个峰值增加，第2 个峰值不断减小。在固有频率附近，液舱可起到减摇水舱的作用。由图中可以看到，当液舱液量较低时，频域计算结果与试验计算结果相差较大，这是由于粘性的影响很大，尽管加入了液舱的阻尼系数来减小忽略粘性带来的影响，但还是存在一定的误差；当液舱液量较高时，惯性力占主导作用。

3.3 耦合结果

图9 给出了3 种液舱液量下船舶纵摇运动的RAO。从图中可以看出，计算结果与试验结果吻合较好，不同液舱液量之间差异很小，这是由于纵摇的纵向惯性矩很大，远大于液舱晃荡引起的波动影响，液舱的加入对船舶纵摇的影响较小。

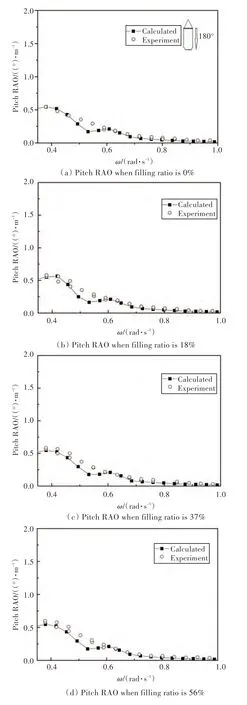
图9 不同液量下纵摇运动RAO 实验值与计算值对比（迎浪）Fig.9 Comparison of pitch RAO of experimental results and computational results at different filling levels（head sea）

液舱内液体粘性对船舶横摇的影响显著，因此有必要计算船舶与液舱晃荡时域耦合运动。船舶运动的RAO 可以通过傅立叶变换来与前面的计算结果相比较。

图10 给出了3 种液舱液量下船舶横摇运动RAO 时域、频域计算结果和试验数据三者的对比。可以看出，频域计算对与某些频域点对应的RAO 值预测过高，而时域计算则考虑了液舱内液体的非线性影响，起到了很好的削峰作用；当液舱液量为18%时，液舱的固有频率为0.49 rad/s，与船舶固有频率很相近, 其峰值的位置从0.5 rad/s 移动到0.6 rad/s，但峰值几乎没变。当液舱液量为37%和56%时，结合图8 能够观察到明显的2 个峰值的分离。当液舱的固有频率远离船舶固有频率时，液舱能起到减摇水舱的作用，并且随着两种频率相差越大，减摇效果更明显。当液舱液量较低时，由于考虑了液舱内流体粘性以及自由液面的非线性影响，RAO 的时域耦合计算结果和频域耦合计算结果相比与试验结果更接近。当液舱液量较高时，舱内流体惯性的影响相对粘性影响占主导作用，2 种方法的求解准确度差异不大。

图10 不同液量下横摇运动RAO 实验结果、时域和频域计算结果对比（横浪）Fig.10 Comparison of roll RAOs of experimental and computational results（frequency domain and time domain）at different filling levels（beam sea）

4 结 语

船舶在波浪中运动会激励液舱内液体产生晃荡，而液舱晃荡力又会对船舶运动姿态产生影响，相互间产生耦合作用。本文建立了在波浪载荷下考虑液舱内流体粘性阻尼时船体与液舱晃荡的时域耦合运动数值计算方法。首先，基于频域势流理论得到水动力系数以及波浪载荷，基于IRF 法在时域积分得到波浪辐射力。随后，一方面通过CFD 计算获取液舱晃荡所产生的力及力矩加载于船体，另一方面，在船舶运动仿真计算结果的基础上计算液舱晃荡运动。最后，对FPSO 船型在不同液量下的时域耦合运动进行计算，并与频域和试验结果进行了对比分析。

对采用IRF 法求解时域波浪辐射力过程中截断误差影响的研究表明，在时间较早时，迟滞方程数值较大，截断误差的影响较小，到后期，截断误差的影响逐渐增大。此外，与试验数据的对比研究表明，在不同液舱液量条件下，系统阻尼比γ =0.1～0.15 时能够得到较好的计算结果。在耦合运动方面，液舱内液体的粘性对耦合作用有较大影响：低液量时，粘性的影响相对惯性影响占主导作用，横摇运动RAO 的时域耦合计算结果和频域耦合结果相比与试验值更接近；高液量时，惯性影响较粘性影响更加重要，时域和频域这2 种计算方法的求解精度差异不大。本文中计算方法可作为FPSO 或相关船型液舱晃荡和船舶耦合运动模拟的参考。

［1］MOLIN B，REMY F，LEDOUX A，et al. Effect of roof impacts on coupling between wave response and slosh⁃ing in tanks of LNG-carriers［C］//ASME 2008 27th In⁃ternational Conference on Offshore Mechanics and Arc⁃tic Engineering.Estoril，Portugal，2008：15-24.

［2］CUMMINS W E. The impulse response function and ship motions［R］. The Symposium on Ship Theory，Hamburg，Germany，1962.

［3］KIM Y，NAM B W，KIM D W，et al. Study on cou⁃pling effects of ship motion and sloshing［J］. Ocean En⁃gineering，2007，34（16）：2176-2187.

［4］李裕龙，朱仁传，缪国平，等.基于OpenFOAM 的船舶与液舱流体晃荡在波浪中时域耦合运动的数值模拟［J］.船舶力学，2012，16（7）：750-758.LI Yulong，ZHU Renchuan，MIAO Guoping，et al.Simulation of ship motions coupled with tank sloshing in time domain based on OpenFOAM［J］. Journal of Ship Mechanics，2012，16（7）：750-758.

［5］洪亮，朱仁传，缪国平，等.波浪中船体与液舱晃荡耦合运动的时域数值计算［J］. 哈尔滨工程大学学报，2012，33（5）：635-647.HONG Liang，ZHU Renchuan，MIAO Guoping，et al.Numerical calculation of ship motions coupled with tank sloshing in time domain based on potential flow theory［J］. Journal of Harbin Engineering University，2012，33（5）：635-647.

［6］黄硕，段文洋，马庆位，等.液舱晃荡及其与船舶耦合运动问题的研究进展［J］. 船舶力学，2013，17（10）：1209-1220.HUANG Shuo，DUAN Wenyang，MA Qingwei，et al.Research progress on sloshing and coupling motion of sloshing and ship［J］. Journal of Ship Mechanics，2013，17（10）：1209-1220.

［7］CLAUSS G F，TESTA D，SPRENGER F. Coupling ef⁃fects between tank sloshing and motions of a LNG carri⁃er［C］// Proceedings of the ASME 2010 29th Interna⁃tional Conference on Ocean，Offshore and Arctic Engi⁃neering.Shanghai，China，2010.

［8］LOOTS E，PASTOOR W，BUCHNER B，et al. The numerical simulation of LNG sloshing with an im⁃proved volume of fluid method［C］// Proceedings of OMAE04 23rd International Conference on Offshore Mechanics and Arctic Engineering. Vancouver，British Columbia，Canada，2004.

［9］LEE D H，KIM M H，KWON S H，et al. A parametric sensitivity study on LNG tank sloshing loads by numeri⁃cal simulations［J］.Ocean Engineering，2007，34（1）：3-9.

［10］张书谊，段文洋. 矩形液舱横荡流体载荷的Fluent 数值模拟［J］. 中国舰船研究，2011，6（5）：73-77.ZHANG Shuyi，DUAN Wenyang. Numerical simula⁃tion of sloshing loads on rectangular tank based on Fluent［J］. Chinese Journal of Ship Research，2011，6（5）：73-77.

［11］金晶，薛鸿祥，唐文勇，等.大型补给舰船液舱晃荡载荷计算方法［J］.中国舰船研究，2012，7（6）：50-56.JIN Jing，XUE Hongxiang，TANG Wenyong，et al.Calculation procedure of sloshing loads for large-scale depot ships［J］. Chinese Journal of Ship Research，2012，7（6）：50-56.