平均值不等式的引伸
2022-10-09武汉软件工程职业学院430205刘小宁
武汉软件工程职业学院(430205) 刘小宁

和平均值不等式

等号成立当且仅当a1= a2=···= an.
基于变量替换[1],本文引伸了平均值不等式(1),得到6个关于平均值中变量ai个数n的不等式,并举例说明其应用.
定理1An与Gn之间存在如下两个不等式

等号成立当且仅当a1= a2=···= an.
证明设xi为正数, xi的个数n≥2,当i = 1,2,···,n时,由式(1)得关于xi的算术—几何平均值不等式

式(4)等号当且仅当x1= x2=···= xn时成立.
1)对式(4)进行变量替换,令x1= x2=···= xn-1=Gn-1,xn= an得

而

将式(6)代入式(5)中整理得到式(2),根据式(1)等号成立的条件,可知式(2)等号当且仅当x1= x2=···=xn-1= Gn-1= xn= an,即a1= a2=···= an时成立.
2)对式(4)进行变量替换,令x1= x2=···= xn-1=An-1,xn= an得

而

将式(8)代入式(7)中整理得到式(3),根据式(1)等号成立的条件,可知式(3)等号当且仅当x1= x2=···= xn=An-1= an,即a1= a2=···= an时成立.
式(2)和式(3)分别是Rado不等式和Popovic不等式[2-3],与参考文献[4-8]相比,文中根据著名的平均值不等式(1),采用变量替换的证明方法是比较简明的.
定理2An与Hn之间存在如下两个不等式

等号成立当且仅当a1= a2=···= an.
证明设xi为正数, xi的个数n≥2,当i = 1,2,···,n时,由式(1)得关于xi的算术—调和平均值不等式

式(11)等号当且仅当x1= x2=···= xn时成立.
1)对式(11)进行变量替换,令x1= x2=···= xn-1=Hn-1,xn= an得
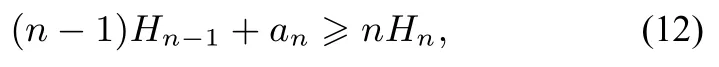
将式(6)代入式(12)中整理得到式(9),根据式(1)等号成立的条件,可知式(9)等号当且仅当x1= x2=···= xn-1=Hn-1= xn= an,即a1= a2=···= an时成立.
2)对式(11)进行变量替换,令x1= x2=···= xn-1=An-1,xn= an得An≥,即
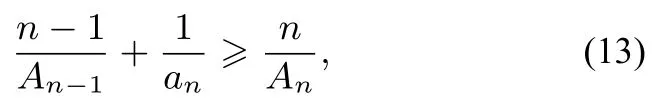
而

将式(14)代入式(13)中整理得到式(10),根据式(1)等号成立的条件,可知式(10)等号当且仅当x1= x2=···=xn-1= An-1= xn= an,即a1= a2=···= an时成立.
定理3Gn与Hn之间存在如下两个不等式

等号成立当且仅当a1= a2=···= an.
证明设xi为正数, xi的个数n≥2,当i = 1,2,···,n时,由式(1)得关于xi的几何—调和平均值不等式
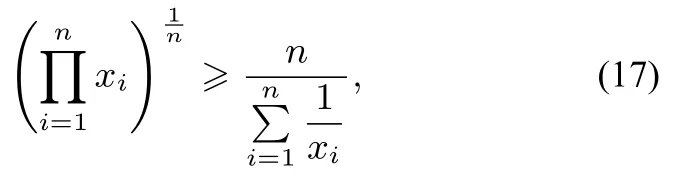
式(17)等号当且仅当x1= x2=···= xn时成立.
1)对式(17)进行变量替换,令x1= x2=···= xn-1=Gn-1,xn= an,得
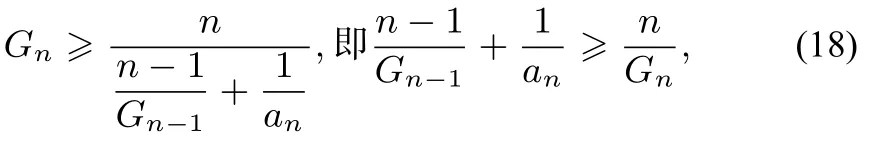
将式(14)代入式(18)中整理得到式(15),根据式(1)等号成立的条件,可知式(15)等号当且仅当x1= x2=···=xn-1= Gn-1= xn= an,即a1= a2=···= an时成立.
2)对式(17)进行变量替换,令x1= x2=···= xn-1=Hn-1,xn= an,得

将式(8)代入式(19)中整理得到式(16),根据式(17)等号成立的条件,可知式(16)等号当且仅当x1= x2=···=xn-1= Hn-1= xn= an,即a1= a2=···= an时成立.
显然,定理1~3是算术—几何—调和平均值不等式(1)的引伸,利用定理1—定理3,可以导出一些有趣的不等式.
将不等式(3)与(16)两边分别相乘,可得:
例1An与Hn之间有如下不等式成立

等号成立当且仅当a1= a2=···= an.
将不等式(2)与(9)两边分别相加,可得:
例2An、Gn与Hn之间存在如下不等式

等号成立当且仅当a1= a2=···= an.
将不等式(10)与(15)两边分别相加,可得:
例3An、Gn与Hn之间成立如下不等关系

等号成立当且仅当a1= a2=···= an.
