水下航行器固有频率模型的可靠性分析

刘克勤，李天匀，朱翔，黄惜春

1 华中科技大学船舶与海洋工程学院，湖北武汉430074

2 中国舰船研究设计中心，湖北武汉430064

0 引 言

利用有限元模型对工程结构进行仿真分析在工程中已经得到了广泛的应用，在有限元模型的基础上还可对结构进行优化设计和性能预报。然而使用有限元模型模拟工程实际结构时不可避免地存在误差，如果误差很大甚至远远超过工程误差的允许范围，则有限元模型是不可靠的，因而基于有限元模型所做的任何分析都缺乏可信度。一般认为工程试验得到的结果具有较高的可靠性，因此将试验结果作为有限元模型的评判标准，在此基础上对原有的有限元模型进行修改，使得有限元模型的计算结果更接近试验结果，这就是有限元模型的修正。有限元模型确认在有限元模型修正的基础上，进一步量化模型中的不确定性和传递特性，通过统计意义下的模型修正来校准参数［1］，预报和估计有限元模型计算结果与工程实际的差异，并全面评估有限元模型的精度和计算结果的可信度［2］，最终得到可靠的有限元模型。

模型修正始于20 世纪50年代航空航天业，现已广泛应用于航空航天、土木、汽车等工程领域。早期的有限元模型修正使用矩阵型修正方法，对有限元模型的质量、刚度或阻尼矩阵的元素进行修正，但矩阵型修正法在修正后，矩阵缺乏明确的物理意义，难以保存原模型的链接信息，计算效率低，难以在工程复杂的结构中应用。现在工程领域中广泛使用的是设计参数型修正法，该方法是对有限元模型中设置的实际物理参数进行修正，结合大型有限元分析软件，使得运用设计参数型修正法进行模型修正更加实用。20 世纪90年代模型修正在统计学的基础上进一步向模型确认发展，美国机械工程师学会等都发布过模型修正和确认的技术框架。模型修正和确认在工程实际领域也得到了广泛应用，如Zang 等［3］对航空发动机部件及整机模型进行了模型修正与确认；Dascotte［4-5］对轿车车身的有限元模型进行了修正；夏品奇等［6］基于固有频率和模态振型对新加坡Safti大桥模型进行了修正。

近年来，国内开始引入有限元模型修正和确认的概念并将其应用到了工程领域中，如郭勤涛等［7-8］对国内外有限元模型修正和确认的研究情况进行过详细介绍；而后与张冬冬等［9-11］共同就分级确认、代理模型、确认准则等有限元模型的确认方法进行了研究，并将其应用于工程实际模型中；宗周红等［12-13］较完整地运用有限元模型修正和确认方法，对包括下白石大桥在内的多座桥梁的有限元模型进行了修正和确认。在船舶领域，童宗鹏等［14］通过频响函数相关系数灵敏度的分析方法，以发动机和轴系支撑刚度为修正参数，对舰艇模型的有限元模型进行了修正；温华兵等［15］也通过相似的方法以隔振器刚度为修正参数对浮筏舱段结构有限元模型做出修正，修正后的频响函数更加趋近于试验结果。

本文将基于有限元模型修正和确认理论方法，对水下航行器有限元模型的可靠性进行分析。本文将有限元模型部分结构的弹性模量和密度作为修正参数，以前四阶弯曲振动固有频率作为响应特征，建立多项式函数响应面模型。使用蒙特卡罗模拟抽取50 万组修正参数代入响应面模型，计算弯曲振动固有频率。根据核密度估计对水下航行器前四阶弯曲固有频率的概率分布进行预报，用于和试验结果对比，以判断模型的可靠性。

1 有限元模型修正与确认

图1 为模型修正与确认的基本流程，该流程基于响应面函数的设计参数型有限元模型。

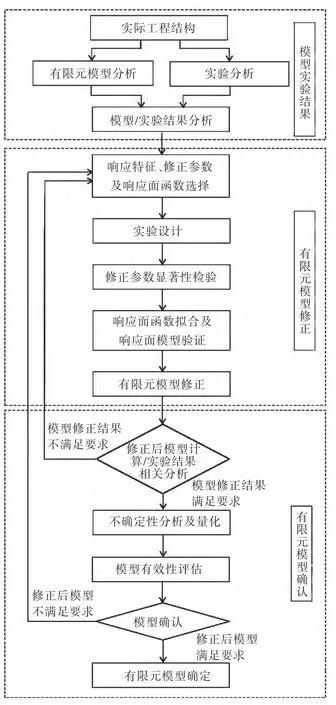
图1 基于响应面的有限元模型修正与确认基本流程Fig.1 The process of finite element model updating and validation based on response surface

1.1 响应面模型

响应面模型将复杂的有限元模型计算过程简化为简单的修正参数与响应特征值之间的函数关系，使用响应面函数代替有限元模型进行计算可以提高模型的计算效率，其中响应特征为响应面函数的因变量，修正参数为响应面函数的自变量。

建立响应面模型需要选择修正参数变量空间中的一组样本点，用于对有限元模型进行拟合，通过中心复合试验设计可以选择合适的样本点，从而用较少的样本去获得理想的响应面模型，这种方法适用于低阶响应面模型［2］。中心复合试验设计共分为3 个部分，选择样本的数量与修正参数的个数n 有关。第1 部分包括1 组样本，要求每个修正参数都在取值范围的中心处取值；第2 部分包括2n组样本，要求每个修正参数在最大值或最小值处交叉取值；第3 个部分包括2n 组样本，要求某一个因素取中心值和最大值或最小值的几何平均，其他修正参数和第1 部分相同，在中心处取值，中心复合设计选择样本的数量共有N=1+2n+2n 组。

使用设计参数型修正法进行有限元模型的修正和确认，选择的修正参数应该具有一定的灵敏度，能够显著影响响应特征。根据数理统计相关理论［16］，给出假设H0：假设修正参数不能显著影响响应特征。若假设成立，则检验统计量应满足F分布，根据检验统计量观测值在F 分布中的位置即可得到F 检验值p，p 表示检验统计量取观测值的概率，若检验值p 小于给定的显著水平，则可以拒绝假设H0，认为修正参数能够显著影响相应特征。

得到响应面函数后通过R2检验和相对均方根误差（RMSE）检验，检查响应面模型的拟合情况，R2检验和RMSE 检验计算如式（1）和式（2）所示。

式中：n 为试验设计选取的样本数量；yRi和yi为第i 组样本在响应面函数和有限元模型中对应的响应特征值；为有限元模型中响应特征值的均值。

R2判定系数和RMSE 值都是表征响应面函数拟合效果的无量纲参数，取值范围在0～1 之间。R2取值越趋近于1 或者RMSE 取值越趋近于0 时，响应面函数的拟合效果越好。

1.2 模型可靠性分析

模型确认过程的核心内容是计算模型输出响应结果与试验响应结果的对比过程，根据模型确认准则，实现计算模型可信度评价［17］。由于试验中试件的不确定性、数据测量与数据处理的不确定性以及试验环境的不确定性等原因［2］，试验结果也是不确定的。有限元模型通过设计参数的取值变化来完成特征响应的不确定性分析。假设有限元模型是可靠的，则计算得到的响应特征分布应该和试验结果的分布相近，可以认为两者具有相同的统计分布，因此试验结果应位于有限元模型的预报区间内，此时认为假设成立，有限元模型是可靠的。

蒙特卡罗模拟是目前采用得最为广泛的概率分析方法［13］，使用蒙特卡罗模拟可以量化修正参数的不确定性对响应特征不确定性的影响，通过修正参数的变化得到响应特征的统计分布情况。蒙特卡罗模拟根据修正参数的概率密度函数，从取值区间中选择一定数量的样本代入响应面模型进行计算，通过对响应特征的计算结果统计分析得到响应特征的分布情况。

由于响应特征的分布情况未知，因而采用核密度估计获得响应特征的分布情况。假设xi是样本的观测值，在任意点x 处的总体密度函数的核密度估计fh（x）的定义如式（3）［18］所示：

式中：h 为窗宽；K 为核函数，一般使用高斯核函数。

2 有限元模型可靠性分析

水下航行器有限元模型需要重点关注艉部结构的振动特性，三维模型部分使用梁单元和壳单元详细建模，其他部分则用梁单元简化模拟，梁单元与三维模型间用刚性域连接，结构模型如图2所示［19］。

图2 水下航行器有限元模型Fig.2 The finite element model of the underwater vehicle

2.1 修正参数和响应特征选择

本文选择模型艉舱壁前面部分结构的弹性模量和密度、艉部部分结构的弹性模量和密度4 个量作为修正参数，分别设为X1，X2，X3和X4。由于材料弹性模量和密度数量级相差较大，考虑到响应面模型的需要以及模型自身材料的分布情况，将所有修正参数除以初始值转变为无量纲量。模型艉舱壁前部分在整体模型中所占比重较大，因此艉舱壁前面部分修正参数浮动范围应相对较小。又由于有限元模型重点关注艉部结构的振动特性，因此艉部部分修正参数的浮动范围应相对较大，因而X1和X2的取值区间为［0.9，1.1］，X3和X4的取值区间为［0.7，1.3］。

响应特征选取水下航行器前四阶弯曲固有频率，分别设为Y1，Y2，Y3和Y4。由于模态试验更加容易在空气中进行，故此处模态均指干模态。

2.2 有限元模型计算结果

图3 为有限元模型计算得到水下航行器结构的前四阶弯曲模态云图。

图3 水下航行器前四阶弯曲模态云图Fig.3 The contours of the first four bending mode shapes

2.3 建立响应面模型

采用中心复合试验设计法选择25 组修正参数代入到有限元模型中进行计算，修正参数取值情况和计算结果如表1 所示。

根据以上样本进行方差分析，各响应特征和各修正参数之间的F 检验值如表2 所示。

表中F 检验值结果最大仅为3.4×10-7，即上述数据表明修正参数对响应特征影响不显著这一假设成立的概率最大仅为0.000 034%，因此可以拒绝假设，认为所有修正参数对响应特征都有显著的影响。

根据样本使用三次多项式函数对4 个响应特征进行拟合，拟合后的R2检验和RMSE 检验结果如表3 所示。

表3 中R2判定系数均基本等于1，RMSE 值均接近于0，表明使用三次多项式建立的响应面模型拟合效果很好。

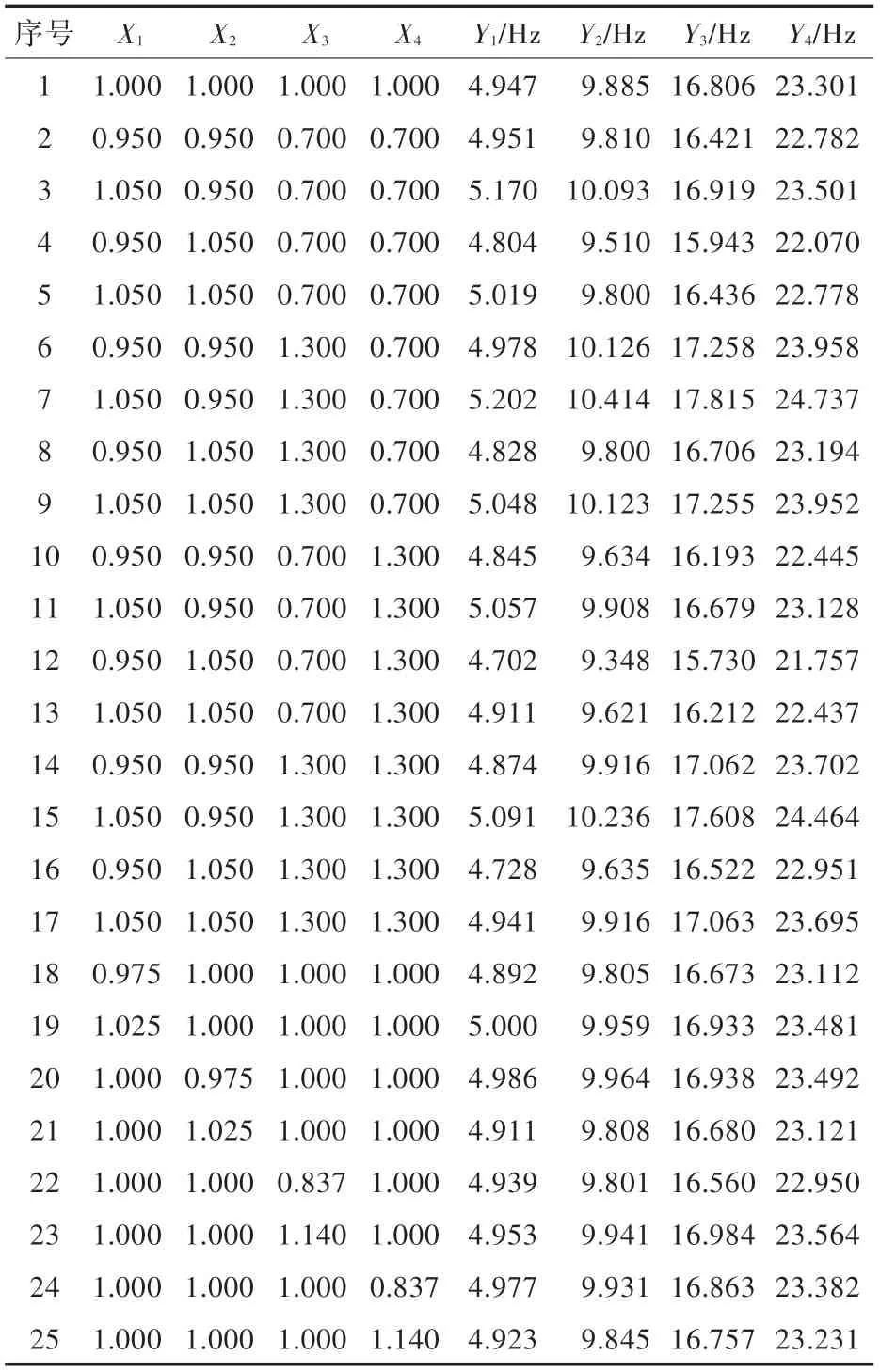
表1 试验设计与计算结果Tab.1 The results of experiment and calculation

表2 响应特征和修正参数之间的F 检验值Tab.2 The F-test value of responses and parameters

表3 多项式拟合检验Tab.3 The results of polynomial fitting test

2.4 特征频率参数估计

假设修正参数在取值区间内均匀分布，选择若干组修正参数带入响应面模型中进行计算，经验证，当蒙特卡罗模拟次数达到50 万次以上时，所有预报区间均可以精确到小数点后2 位数字，故此处选择50 万组修正参数代入响应面模型中进行计算。利用核密度估计法对计算结果进行统计分析，得到4个响应参数的概率密度函数（图4）。

图4 响应参数概率密度函数Fig.4 Probability density function of responses

表4 为前四阶弯曲固有频率在置信度分别为0.90 和0.95 时的置信区间，此时假设水下航行器有限元模型可靠。

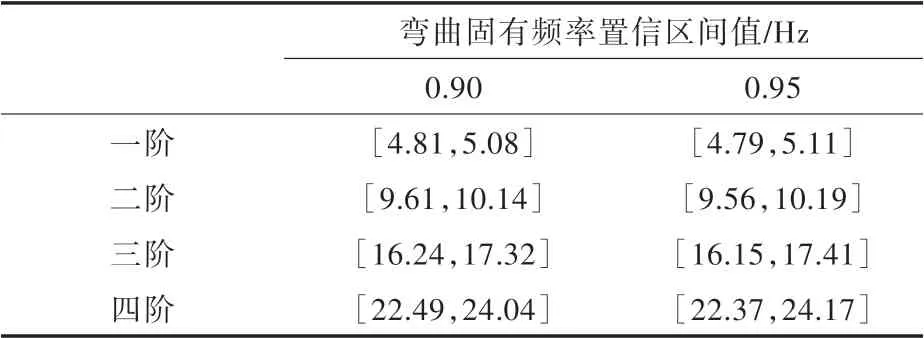
表4 前四阶弯曲固有频率的置信区间Tab.4 The interval estimate of the first four bending frequencies

通过对水下航行器进行全尺度试验，得到前四阶弯曲固有频率，将试验结果和表4 进行比对。表中置信度为0.90 时水下航行器一阶弯曲振动固有频率取值范围为4.81～5.08 Hz，表明水下航行器有限元模型可靠这一假设成立时，模态试验得到水下航行器一阶弯曲固有频率在4.81～5.08 Hz区间内的概率为90%，如果试验结果满足要求，则可以判断有限元模型是可靠的。上表给出了基于目前有限元模型得到的水下航行器前四阶弯曲固有频率的置信区间，如果试验结果均能位于预报区间内，则可以认为该有限元模型能够反映水下航行器的振动特性，现有的有限元模型是可靠的。

3 结 语

本文将有限元修正和确认的相关理论引入到水下航行器有限元模型的分析中，建立多项式响应面模型，给出了水下航行器前四阶弯曲振动固有频率的区间估计，提出以弯曲固有频率试验结果是否处于预报区间作为判断有限元模型可靠性的依据。该方法可推广用于判断长宽比较大的船舶有限元模型的可靠性。

［1］宗周红，任伟新. 桥梁有限元模型修正和模型确认［M］.北京：人民交通出版社，2012.

［2］李辉，丁桦.结构动力模型修正方法研究进展［J］.力学进展，2005，35（2）：170-180.LI Hui，DING Hua. Progress in model updating for structural dynamics ［J］. Advances in Mechanics，2005，35（2）：170-180.

［3］ZANG C P，EWINS D J. Model validation for structur⁃al dynamics in the aero-engine design process［J］.Frontiers of Energy and Power Engineering in China，2009，3（4）：480-488.

［4］DASCOTTE E. Linking finite element analysis and test：case study in automobile industry［C］//Proceed⁃ings of 11th International Modal Analysis Conference.Florida，USA，1993：456-461.

［5］DASCOTTE E. Application of sensitivity analysis and finite element model tuning on a car body［C］// Pro⁃ceedings of the 15th International Seminar On Modal Analysis and Structural Dynamics. Leuven，Belgium，1990：483-393.

［6］夏品奇，BROWNJOHN J M W.斜拉桥有限元模型与建模修正［J］.振动工程学报，2003，16（2）：219-223.XIA Pinqi，BROWNJOHN J M W. Finite element mod⁃eling and model updating of a cable-stayed bridge［J］.Journal of Vibration Engineering，2003，16（2）：219-223.

［7］郭勤涛，张令弥，费庆国. 结构动力学有限元模型修正的发展——模型确认［J］.力学进展，2006，36（1）：36-42.GUO Qintao，ZHANG Lingmi，FEI Qingguo. From FE model updating to model validation：advances in model⁃ing of dynamic structures［J］. Advances in Mechanics，2006，36（1）：36-42.

［8］郭勤涛，张令弥.结构动力学有限元模型确认方法研究［J］.应用力学学报，2005，22（4）：572-578.GUO Qintao，ZHANG Lingmi. Finite element model validation in structural dynamics［J］. Chinese Journal of Applied Mechanics，2005，22（4）：572-578.

［9］郭勤涛，张令弥.以冲击响应谱为响应特征的有限元模型确认［J］.振动与冲击，2005，24（6）：32-36.GUO Qintao，ZHANG Lingmi. FE model validation us⁃ing shock response spectrum as response feature［J］.Journal of Vibration and Shock，2005，24（6）：32-36.

［10］张冬冬，郭勤涛. Kriging 响应面代理模型在有限元模型确认中的应用［J］. 振动与冲击，2013，32（9）：187-191.ZHANG Dongdong，GUO Qintao. Application of Krig⁃ing response surface in finite element model validation［J］. Journal of Vibration and Shock，2013，32（9）：187-191.

［11］朱跃，张令弥，郭勤涛. 基于SVR 方法的有限元模型确认中不确定性建模研究［J］. 振动与冲击，2010，29（9）：119-122，150.ZHU Yue，ZHANG Lingmi，GUO Qintao. SVR based uncertainty modeling method for structures finite ele⁃ment model validation［J］. Journal of Vibration and Shock，2010，29（9）：119-122，150.

［12］宗周红，高铭霖，夏樟华.基于健康监测的连续钢构桥有限元模型确认（I）——基于响应面法的有限元模型修正［J］.土木工程学报，2011，44（2）：90-98.ZONG Zhouhong，GAO Minglin，XIA Zhanghua. Fi⁃nite element model validation of the continuous rigid frame bridge based on structural health monitoring-PartⅠ：FE model updating based on the response surface method［J］.China Civil Engineering Journal，2011，44（2）：90-98.

［13］宗周红，高铭霖，夏樟华.基于健康监测的连续钢构桥有限元模型确认（Ⅱ）——不确定性分析与模型精度评价［J］.土木工程学报，2011，44（3）：85-92.ZONG Zhouhong，GAO Minglin，XIA Zhanghua. Fi⁃nite element model validation of the continuous rigid frame bridge based on structural health monitoring⁃Part Ⅱ：uncertainty analysis and evaluation of model accuracy［J］. China Civil Engineering Journal，2011，44（3）：85-92.

［14］童宗鹏，章艺，沈荣瀛，等. 基于频响函数灵敏度分析的舰艇模型修正［J］. 上海交通大学学报，2005，39（11）：1847-1850.TONG Zongpeng，ZHANG Yi，SHEN Rongying，et al.Submarine finite element model updating method based on frequency response functions of vibration［J］. Journal of Shanghai Jiao Tong University，2005，39（11）：1847-1850.

［15］温华兵，王国治. 基于频响函数相关系数灵敏度的浮筏舱段有限元模型修正［J］. 江苏科技大学学报（自然科学版），2005，19（6）：75-78.WEN Huabing，WANG Guozhi. Updating finite ele⁃ment model of cabin with floating raft through sensitiv⁃ity analysis of FRF correlation coefficient［J］. Journal of Jiangsu University of Science and Technology（Nat⁃ural Science Edition），2005，19（6）：75-78.

［16］于寅.高等工程数学［M］.武汉：华中理工大学出版社，2001.

［17］REBBA R，MAHADEVAN S. Computational meth⁃ods for model reliability assessment［J］. Reliability Engineering and System Safety，2008，93（8）：1197-1207.

［18］谢中华. MATLAB 统计分析与应用：40 个案例分析［M］.北京：北京航空航天大学出版社，2010.

［19］冯国平，谌勇，黄修长，等. 舰艇艉部纵向激励传递特性分析［J］. 噪声与振动控制，2009，29（6）：132-135.FENG Guoping，CHEN Yong，HUANG Xiuchang，et al. Study on transmission paths in submarine stern ex⁃cited longitudinally［J］. Noise and Vibration Control，2009，29（6）：132-135.