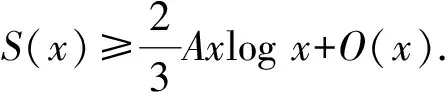一类数论函数的均值估计

郭 颖, 鲁思彤, 马 晶

(吉林大学 数学学院, 长春 130012)

0 引 言

Dirichlet证明了

文献[4-5]分别改进了文献[3]中关于一般数论函数的结果: 文献[4]证明了若有α∈[0,1),θ≥0, 使得f(n)≪nα(logn)θ, 则

文献[5]证明了如果数论函数f满足Ramanujan假设f(n)≪nε(n≥1), 则

文献[6]对Euler函数φ讨论了类似的均值, 证明了

(1)

受文献[6]研究工作的启发, 本文对满足适当条件的一般数论函数f给出Sf(x)的界, 得到如下主要结果:

(2)

则当x→∞时, 有

(3)

易见, 式(1)可作为定理1的直接推论.记f(x)=O(g(x))或f(x)≪g(x)表示存在一个正的常数A(与x无关), 使得对所有充分大的x都有不等式|f(x)|≤Ag(x).函数[·]表示向下取整函数, [1/4]=0.关于指数对理论可参见文献[13].

1 预备命题

设ψ(t)∶=t-[t]-1/2,δ∈{0,1}, 对任意的x≥2和1≤D≤x, 定义

记e(x)=exp{x}=ex.

引理1[14]对x≥1,H≥1, 有

其中e(t)∶=e2πit,Φ(t)∶=πt(1-|t|)cot(πt)+|t|, 并且余项RH满足

命题1

Sδ(x,D)≪(xκD1+λ)1/(κ+1)+xκD1-2κ+λlogx+x-1D3,

(4)

其中(κ,λ)是指数对.

记

由引理1可得

其中H≥1.记

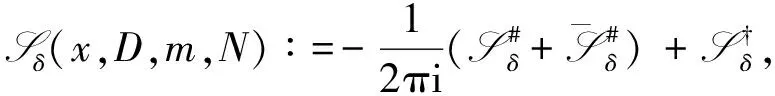
(6)

其中

其中

因此, 对H≥1, 有

(8)

结合式(6)～(8)可得

Sδ(x,D,m,N)≪NH-1+xκN-2κ+λHκ+x-1mN2.

(9)

最后, 利用引理2消去参数H.对H≥1,H的取值范围为[1,N], 用引理2对式(9)进行优化, 得

将式(10)代入式(5), 可得

注意到对里层m求和时, 应用到

因此式(4)成立.证毕.

2 定理1的证明

令D∈[1,x1/2)为待定参变量,Sf(x)可分为两部分:

Sf(x)∶=S1(x)+S2(x),

(12)

(13)

又由已知条件式(2)可得

(15)

且

(16)

此时, 记

将式(15)～(17)代入式(14), 可得

S2(x)≤Axlog(x/N)+O(x4/3N-1+xN-1/2logx+x2N-3).

(18)

最后, 将式(13)，(18)代入式(12)可得

Sf(x)≤xlogN+Axlog(x/N)+O(x4/3N-1+xN-1/2logx+x2N-3+x).

取N=x1/3得

记

记Dk∶=D/2k,K为满足DK+1<1≤DK的整数.通过二分法分离变量和命题1代入指数对(κ,λ)=(1/2,1/2), 有

将式(20)代入式(19), 可得

S(x)≥AxlogD+O(x1/3D+x1/2D1/2logx+x-1D3).