一类变系数时滞微分方程零解的稳定性①

刘 彪， 温艳华

(安徽大学数学科学学院，安徽合肥230601)

0 引言及主要结果

稳定性理论是泛函微分方程的重要理论之一．在系统运行过程中，稳定性是很多系统设计者所期望的性质．因此判断系统的稳定性是众多学者研究的方向之一．线性微分方程

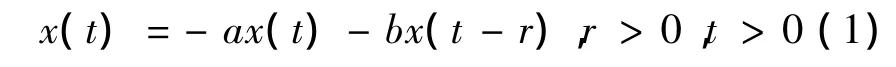
是很典型的时滞方程，其中a，b是常数．方程(1)有多种方法判断其零解的稳定性．首先，如果特征方程的所有根都具有负实部，则方程(1)的零解是渐近稳定的．但由于方程(2)是超越方程，没有好的方法判断其所有根是否都具有负实部，所以这种判断方具有应用上的局限性．

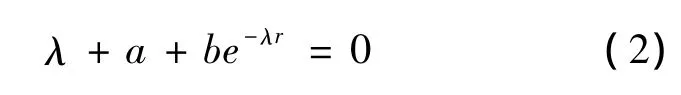
其次，判断方程(1)零解稳定的方法是Lyapunov函数方法(拉什米辛判别法)．对于时滞方程

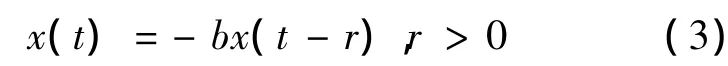
其特征方程为

该Lambert W －函数的解W(t)满足，λr=W(－br)．即λ．由Lambert函数的性质知，当＜0时，W(－br)＜0，从而特征根λ＜0，于是方程(3)零解x=0是渐近稳定的．

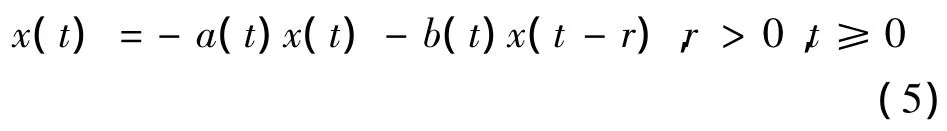
受方程(1)和(3)研究方法启发，本文研究如下的变系数的时滞微分方程的零解的稳定性，其中系数a(t)，b(t)∈C[0，+∞)，利用李亚普诺夫函数方法(拉什米辛判别法)可知，当a(t)＞|b(t)|时，方程(5)的零解x=0是渐进稳定的．事实上，a(t)＞|b(t)|是方程(5)零解稳定性的充分条件，不是必要条件．

1 预备知识

定义 1．1 Lambert函数 W(t)是满足方程[4～5]性质

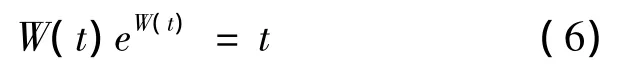
1．1 Lambert函数W(t)有以下性质:

(1)在区间[0，+∞)上，W(t)≥0且单调增加;

引理1．1 考虑时滞微分方程

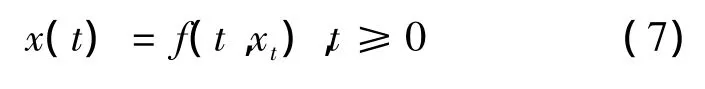
其中f(t，0)=0，f: RR ×C→ RRn把 RR ×(C中的有界集)映入 RRn中的有界集．如果存在K－类函数u，v∈K，函数ω: RR+→ RR+连续和存在一个连续函数V: RR× RRn→R使得t∈ RR，x∈ RRn时成立

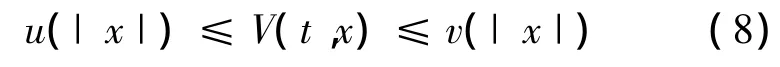
且存在一个连续非减函数p(s)＞s，其中s＞0，当条件 V(t+ θ，φ(θ))≤ p(V(t，φ(0)))，θ∈[－ r，0]成立时，有

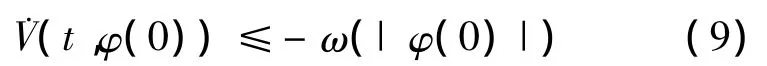
则方程(8)的解x=0 是一致渐近稳定的[2，3]．

2 主要结果

在本节中，我们将在较弱的条件下给出方程(6)零解稳定的判别法．

定理2．1 考虑时滞微分方程(5)，当条件b(t)＞0且成立时，方程(5)的解x=0是渐进稳定的．

证明: 由于a(t)，b(t)是连续函数，且t＞0方程(5)的解是可微的，所以当t＞r时成立

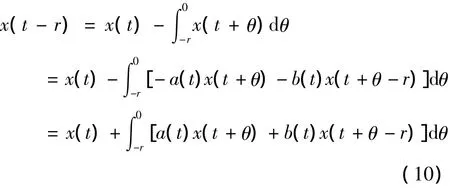
于是，当t＞r时，方程(5)可化为

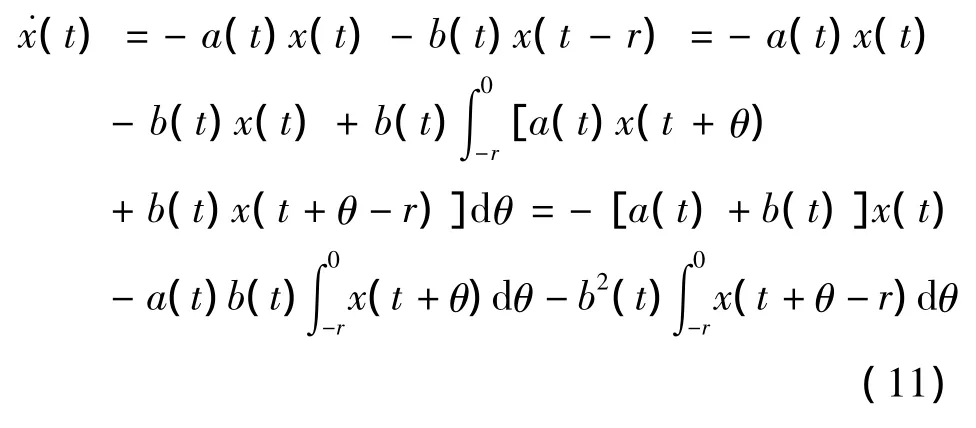
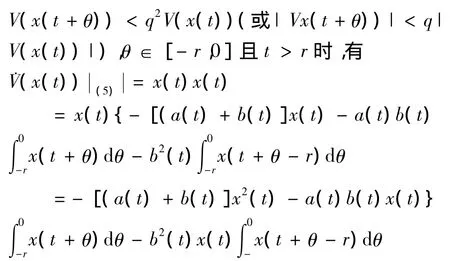
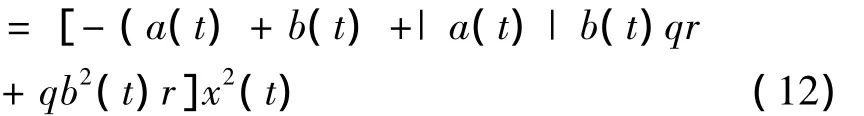
推论2．1 考虑常系数时滞微分方程(1)，当条件b＞0且r成立时，方程(1)的零解x=0是渐进稳定的．

3 例 题

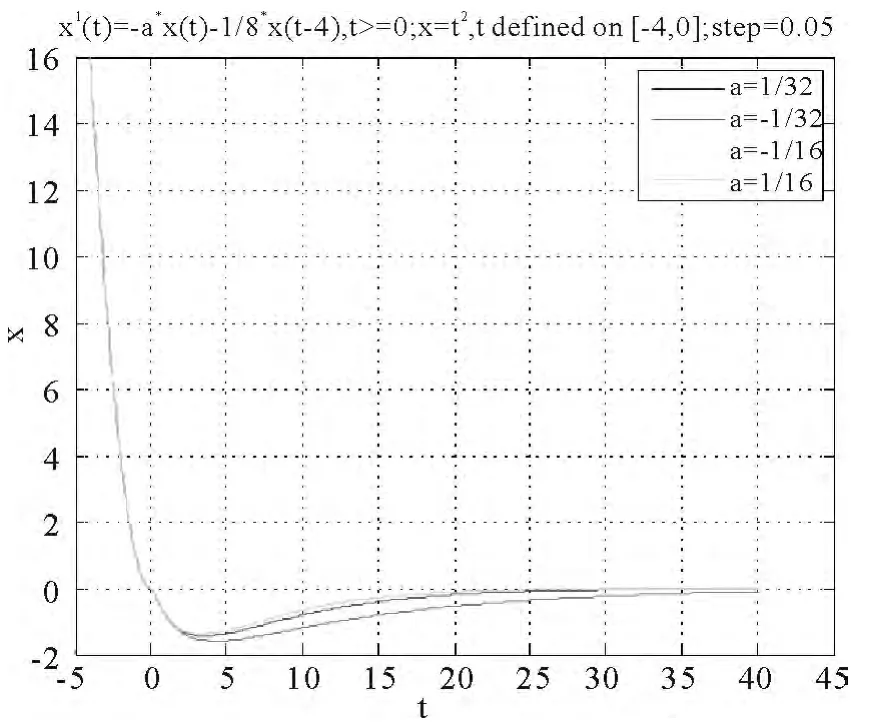
图1

由图1可见此时方程的零解是渐近稳定的．

说明3．1 容易看出，在例3．1．中，a，b不满足条件:a＞|b|，但是我们根据推论1．1．得到常系数时滞微分方程(1)的解x=0是渐近稳定的．

例子3．2 考虑变系数时滞方程

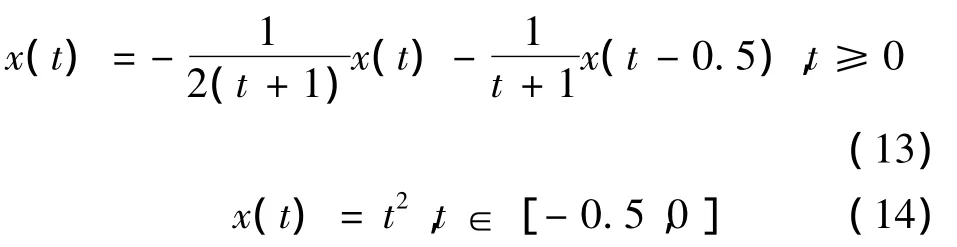
方程(13)(14)的数值模拟如图2所示．

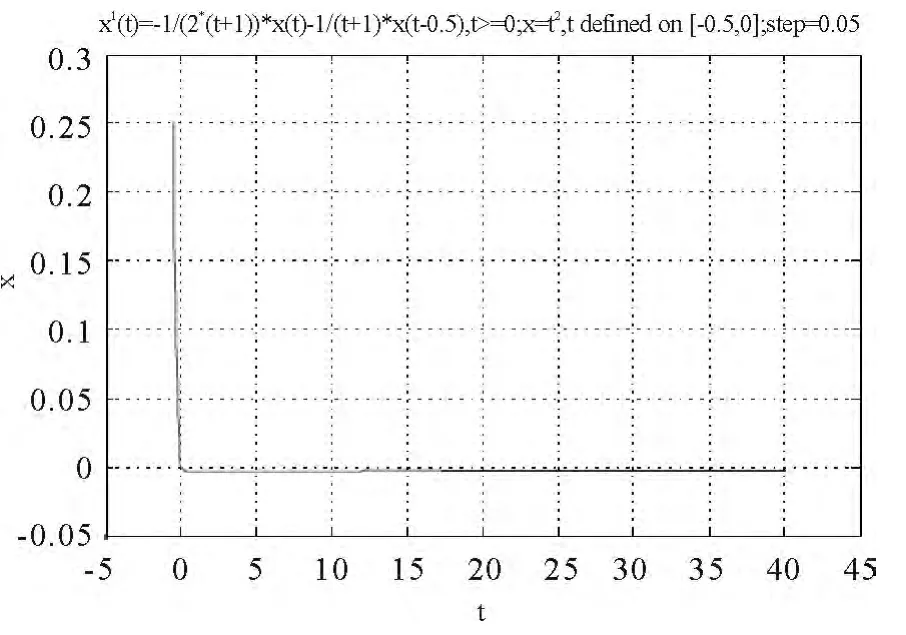
图2

由图2可见方程(14)的零解是渐近稳定的．

[1] 李森林，温立志．泛函微分方程[M]．湖南:湖南科技出版社，1987，120－158．

[2] 郑祖庥．泛函微分方程理论[M]．合肥:安徽教育出版社，1994，256 －268．

[3] Jack K．Hale，B．j．Matkowsky，J．T．Stuart．Introduction to Functional Differential Equat－ ion[M]．New York:Spinger－Verlag，1993:151 －166．

[4] YangQuan Chen，Kevin L．Moore．Analytical Stability Bound for a Class of Delayed Fractional－ Order Dynamic Systems[J]．Nonlinear Dynamics，2002(29):191–200．

[5] W．H．Deng，C．P．Li，Q．Guo．Analysis of Fractional Differential Equations with Multipletime Delays[J]．Nonlinear Dynamics，2007，(48):409 －416．