非线性中立型积分微分方程零解的全局渐近稳定性

黄明辉， 刘 君

(广州城建职业学院 数学教研室， 广东 广州 510925)

1 预备知识

文献[3]利用不动点理论，研究了非线性中立型积分微分方程

(1)

零解的渐近稳定性，其中c可微，τ二次可微且τ′(t)≠1，t∈[0,+∞)。

文献[4]利用不动点理论，研究了时滞非线性中立型积分微分方程

(2)

零解的渐近稳定性，其中c、τ1可微，τ2二次可微且τ2′(t)≠1，t∈[0,+∞)。

受此启发，本文考虑以下非线性中立型积分微分方程零解的全局渐近稳定性：

x′(t)=-a(t)x(t)+c(t)x′(t-τ1(t))+q(t,x(t-τ2(t)),x′(t-τ2(t)))+

(3)

为了给出本文结果，对方程(3)作出以下假设：

(H2) 对任意xi、yi∈R,存在li、hi∈C([0,+∞),R+)，i=1,2，都有

|q(t,x1,y1)-q(t,x2,y2)|≤l1(t)|x1-x2|+l2(t)|y1-y2|,

|f(t,x1,y1)-f(t,x2,y2)|≤h1(t)|x1-x2|+h2(t)|y1-y2|,

其中q(t,0,0)=f(t,0,0)=0,t≥0；

(H3) 存在常数α∈(0,1)，对t≥0，有

此外，对任意t0∈[0,+∞)，设方程(3)的初始函数空间为

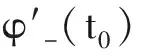
2 主要结论

对任意(t0,φ)∈[0,+∞)×St0,若x∈C1([dt0,+∞))在[t0,+∞)上满足方程(3)，且当t∈[dt0,t0]时，x(t)=φ(t)，则称x为方程(3)经过(t0,φ)的解，记为x(t)=x(t,t0,φ) 。

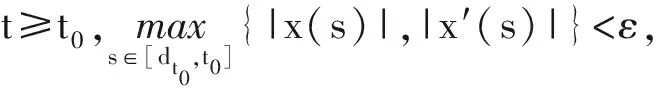
定义2[5]若方程(3)的零解是稳定的，且对任意t0≥0，φ∈St0，都有

则称方程(3)的零解是全局渐近稳定的。

证明对任意t0≥0，设

D={x∈X:x(t)=φ(t),t∈[dt0,t0]},

显然，D为X的一个非空闭子集。定义算子P:D→C([dt0,+∞))如下:对任意x∈D，当t∈[dt0,t0]时，(Px)(t)=φ(t)；当t≥t0时，

q(s,x(s-τ2(s)),x′(s-τ2(s)))]ds+

(4)

首先证明P:D→D。对任意x∈D，当t>t0时，

-a(t)(Px)(t)+c(t)x′(t-τ1(t))+q(t,x(t-τ2(t)),x′(t-τ2(t)))+

(5)

由St0的定义可知，

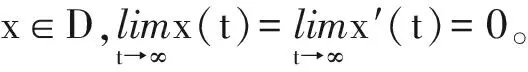
max{|x(t)|,|x′(t)|,|x(t-τi(t))|,|x′(t-τi(t))|}<ε,i=1,2,

(6)

对于(4)式，由(H1)—(H3)和(6)式可知，对任意t≥T以及x∈D，有

|(Px)(t)|≤

此外，存在T1>T，使得对任意t>T1，有

|(Px)′(t)|≤|a(t)(Px)(t)|+|c(t)x′(t-τ1(t))|+

|a(t)(Px)(t)|+|c(t)x′(t-τ1(t))|+l1(t)|x(t-τ2(t))|+

接着证明P:D→D是一个压缩映射。对任意x,y∈D，当t≥t0时，

|q(s,x(s-τ2(s)),x′(s-τ2(s))-q(s,y(s-τ2(s)),y′(s-τ2(s)))|ds]+

(7)

此外，由(5)式、(7)式以及(H3)可知，对任意x,y∈D，当t≥t0时，

|(Px)′(t)-(Py)′(t)|≤|a(t)||(Px)(t)-(Py)(t)|+|c(t)||x′(t-τ1(t))-

y′(t-τ1(t))|+|q(t,x(t-τ2(t)),x′(t-τ2(t)))-q(t,y(t-τ2(t)),y′(t-τ2(t)))|+

(8)

由(7)式和(8)式可知，P:D→D是一个压缩映射。由压缩映射原理可知，P在D中有唯一不动点x。x是方程(3)经过(t0,φ)的唯一解，且满足

(9)

若x(t)=x(t,t0,φ)是方程(3)经过(t0,φ)的一个解，其中|φ|t0<δ，则对任意t≥t0,x(t)=(Px)(t)。可以证明‖x‖t0<ε。否则存在t*>t0,使得max{|x(t*)|,|x′(t*)|} =ε且t

这与t*的定义相矛盾。若|x′(t*)|=ε，则由(H2)、(H3)和(5)式可得

|x′(t*)|≤|a(t*)x(t*)|+c(t*)x′(t*-τ1(t*))+

l1(t*)|x(t*-τ2(t*))|+l2(t*)|x′(t*-τ2(t*))|+

这与t*的定义相矛盾。因此(3)式的零解是稳定的。由(9)式可知，(3)式的零解是全局渐近稳定的。故定理1得证。

3 实 例

为了说明定理1的有效性，下面给出了两个实例。

例1 考虑以下非线性中立型积分微分方程

x′(t)=-a(t)x(t)+c(t)x′(t-τ1(t))+q(t,x(t-τ2(t)),x′(t-τ2(t)))+

(10)

令l1(t)=l2(t)=1/[20(1+t)],h1(t)=h2(t)=1/[10(1+t)],(H2)成立。

注2 文献[3-4]给出的定理不能用于判别(10)式的零解全局渐近稳定。

例2 考虑以下非线性中立型积分微分方程

x′(t)=-a(t)x(t)+c(t)x′(t-τ1(t))+q(t,x(t-τ2(t)),x′(t-τ2(t)))+

(11)

令l1(t)=l2(t)=1/[20(1+t2)],h1(t)=h2(t)=1/[10(1+t2)],(H2)成立。

注3 文献[3-4]给出的定理不能用于判别(11)式的零解全局渐近稳定。