Matlab在判断平面自治系统零解稳定性中的应用
2021-07-20李涧萍范进军
李涧萍 范进军
( 山东师范大学数学与统计学院,250358,济南 )
1 引 言
零解稳定性对微分方程组的定性研究非常重要,在微分方程理论及实际应用中,主要利用Lyapunov直接法对自治系统零解稳定性进行研究[1-3]. 这一方法受制于Lyapunov函数的构造,因为对一般系统很难构造适当的Lyapunov函数. 由平面自治系统理论可知,零解稳定性的问题与所给系统的线素场有关,然而从几何角度来判定零解的稳定性的研究较少. Matlab在微分方程方面有众多应用[4-8]. 本文借助Matlab强大的绘图功能,探究判定零解稳定性的新方法:基于零解稳定性的几何特征,尝试通过Matlab编程,在相平面上绘制出方程的线素场来判定零解的稳定性.
2 预备知识
为了利用Matlab来判断平面自治系统零解的稳定性,本文首先对平面自治系统零解稳定性的定义及其分类进行介绍.
设有自治系统
(1)

假设F∈C(R×G)(G为R2中包含原点的一个区域)且满足解的存在唯一性定理的条件.
易见该系统不显含自变量t,其轨线在相平面上不相交,故在使用Matlab分析图象时只需观察系统在相平面上的轨线特征.
定义1(稳定性[1]) 若对∀ε>0,t0≥0,∃δ=δ(ε,t0)>0,x0∈G,只要‖x0‖<δ,(1)式满足初值x(t0)=x0的解x(t;t0,x0)都在t≥t0上有定义,且当t≥t0时,有‖x(t;t0,x0)‖<ε,则称方程组(1)的零解是稳定的;反之,则不稳定.

∀ε>0,∃T=T(ε,t0,x0)>0,t>t0+T时,‖x(t;t0,t0)‖<ε,
则称方程组(1)的零解是吸引的.
定义3(渐近稳定性[1]) 零解既是稳定的又是吸引的,则称零解是渐近稳定的.


3 Matlab在判断平面自治系统零解稳定性中的应用
由于系统的任意非零解,都可以经过平移变换化为一个新系统的零解,所以判断系统的一个解是否稳定,只需判断新系统的零解是否稳定即可. 为方便起见,假定所给系统有零解. 这样便可以通过Matlab编程,绘制出相平面上原点附近系统的线素场,并观察其走向,以此来分析零解的稳定性.
3.1一般步骤
1) 借助Matlab的Streamslice函数,在相平面上绘制自治系统原点在附近某个邻域U中系统的线素场,初步判断该零解的稳定性.
2) 适当缩小原点附近邻域U的范围,观察以原点为中心的足够小邻域内的线素场的具体走向,进一步判断该系统零解的稳定性.
3.2实例应用下面给出具体例子,通过Matlab编程,判断系统的零解稳定性.
例1判断微分方程组
(2)
零解的稳定性.
解1) 直观说明.为了更充分地观察在原点附近解轨线的具体分布情况,分别取(x,y)∈[-0.5,0.5]×[-0.5,0.5]和(x,y)∈[-0.25,0.25]×[-0.25,0.25],在Matlab中,利用streamslice函数在相平面上绘制出线素场的流线图. Matlab程序如下:
subplot(1,2,1);
[x,y]=meshgrid(linspace(-0.5,0.5));
h=streamslice(x,y,(x-y).*(x.^2+y.^2-1),(x+y).*(x.^2+y.^2-1));
set(h,'Color','b');
xlabel({'x'; '(a)'});ylabel('y');
title('在[-0.5,0.5]×[-0.5,0.5]范围内轨线分布','FontSize',8);
axis equal;
axis([-0.5 0.5 -0.5 0.5]);
subplot(1,2,2);
[x,y]=meshgrid(linspace(-0.25,0.25));
h=streamslice(x,y,(x-y).*(x.^2+y.^2-1),(x+y).*(x.^2+y.^2-1));
set(h,'Color','b');
xlabel({'x'; '(b)'});ylabel('y');
title('在[-0.25,0.25]×[-0.25,0.25]范围内轨线分布','FontSize',8);
axis equal;
axis([-0.25 0.25 -0.25 0.25]).
图1为微分方程组(2)在不同范围内的轨线分布,图中箭头表示轨线的方向. 由图1可知,在原点邻域内的解轨线一致地走向原点,故该系统的零解渐近稳定.

图1 方程组(2)在不同范围的轨线分布
在单位开圆域内是负定的,由引理1知,该系统的零解渐近稳定.
例2 判断微分方程组
(3)
零解的稳定性.
解1)直观说明.分别取(x,y)∈[-1,1]×[-1,1]和(x,y)∈[-0.5,0.5]×[-0.5,0.5],在Matlab中,利用Streamslice函数在相平面上绘制出线素场的流线图. Matlab程序如下:
subplot(1,2,1);
[x,y]=meshgrid(linspace(-1,1));
h=streamslice(x,y,-y-x.*y.^2,x-x.^4.*y);
set(h,'Color','b');
xlabel({'x'; '(a)'});ylabel('y');
title('在[-1,1]×[-1,1]范围内轨线分布','FontSize',9);
axis equal;
axis([-1 1 -1 1]);
subplot(1,2,2);
[x,y]=meshgrid(linspace(-0.5,0.5));
h=streamslice(x,y,-y-x.*y.^2,x-x.^4.*y);
set(h,'Color','b');
xlabel({'x'; '(b)'});ylabel('y');
title('在[-0.5,0.5]×[-0.5,0.5]范围内轨线分布','FontSize',9);
axis equal;
axis([-0.5 0.5 -0.5 0.5]).
由图2可知,在原点附近的解轨线均是闭合的,又原点始终在闭合解轨线的内部,使得轨线不可能一直“走向”原点,故该系统的零解稳定但不渐近稳定.

图2 方程组(3)在不同范围内的轨线分布
由引理1知,该系统的零解稳定.
例3判断微分方程组
(4)
零解的稳定性.
解1)直观说明.分别取(x,y)∈[-1,1]×[-1,1]和(x,y)∈[-0.5,0.5]×[-0.5,0.5],在Matlab中,利用Streamslice函数在相平面上绘制出线素场的流线图. Matlab程序如下:
subplot(1,2,1);
[x,y]=meshgrid(linspace(-1,1));
h=streamslice(x,y,-x.^5-y.^3,-3*x.^3+y.^3);
set(h,'Color','b');
xlabel({'x'; '(a)'});ylabel('y');
title('在[-1,1]×[-1,1]范围内轨线分布','FontSize',9);
axis equal;
axis([-1 1 -1 1]);
subplot(1,2,2);
[x,y]=meshgrid(linspace(-0.5,0.5));
h=streamslice(x,y,-x.^5-y.^3,-3*x.^3+y.^3);
set(h,'Color','b');
xlabel({'x'; '(b)'});ylabel('y');
title('在[-0.5,0.5]×[-0.5,0.5]范围内轨线分布','FontSize',9);
axis equal;
axis([-0.5 0.5 -0.5 0.5]).
由图3可知,在原点任意小的邻域内,方程组的解轨线进入邻域内后,又远离原点走向无穷远处. 故该系统的零解不稳定.
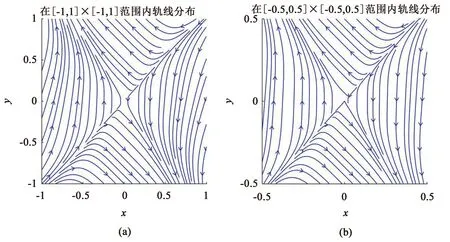
图3 方程组(4)在不同范围内的轨线分布
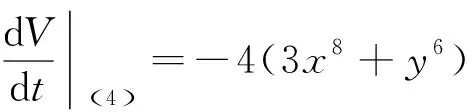
4 结 语
本文从零解稳定性的几何特征出发,基于Lyapunov零解稳定性理论,通过Matlab编程,结合平面自治系统的具体实例,绘制出相应系统的线素场,并观察线素场的走向,以此来分析零解的稳定性. 上述判定方法既直观地反映了平面自治系统零解稳定性的几何性质,又省去了寻找Lyapunov函数的复杂过程,为研究一类难以找到合适Lyapunov函数的自治系统的零解稳定性问题,提供了更为便捷、直观的途径.
