某客车排气系统振动模态分析及悬挂点优化①

吴亚波， 周 鋐

(1．同济大学新能源汽车工程中心，上海201804;2．同济大学汽车学院，上海201804)

0 引言

汽车排气系统作为车辆动力系统重要组成部分，一方面需要满足车辆发动机排气的基本功能，同时另一方面还需要保障排出的废气达到相应的环保指标．此外，排气系统排出废气时所发出的噪音及对于引起的整车地板振动都对整车系统NVH性能有着较大的影响[1]．

在实际工程中，由于发动机自身激励和排气过程产生的气体激励，通过排气系统作用于车身地板振动，并产生乘客舱内噪声．因此，为降低排气管向地板传递的振动能量，可以选择排气管振动相对较小的位置作为挂钩吊耳的悬挂点，这将有利于车辆行驶时降低车内噪声，提高乘客乘坐舒适度感受．

作者采用平均驱动自由度位移对汽车排气管悬挂点布置进行优化[2]，先采用Hypermesh软件对汽车排气系统的振动进行有限元建模，而后利用OptiStruct模块进行排气系统的自由模态分析和模态试验进行自由模态验证，再通过计算得出排气管上各点的平均驱动自由度位移值并尽量选取最小值，从而达到有效降低排气系统振动向车身传递的，进而减小乘员室的振动和噪声问题．

1 模态分析基本理论

模态分析本质上是对系统结构的模态参数的解析过程，而模态参数实则为由质量和刚度构成的矩阵的得出的特征值和特征向量．在实际工程中，系统大多是受到单一激励，故而系统的模态振型是近似将各阶振型按照一定比例叠加的结果．

振动微分方程为:)

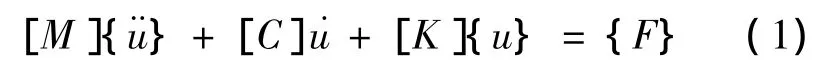
式中，[M]，[C]，[K]分别表示质量矩阵、阻尼矩阵和刚度矩阵，F为外加载荷．当计算系统固有特性时，可忽略阻尼和外加载荷的影响．故

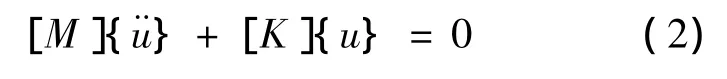
上述方程有非零解的条件是特征方程为零．即

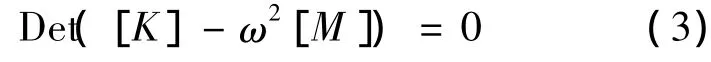
由(3)式可以看出，N自由度系统有N个固有频率与之对应．对应的特征向量即为相应的模态振型．

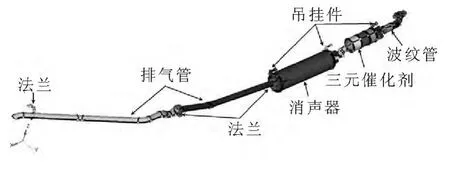
图1 排气系统有限元模型

在计算排气系统的模态时，考虑到排气系统自身的复杂，所以采用有限元的方法，将排气系统细分为有限个小单元，然后算出各单元的模态之后再进行近似累加即可．

2 客车排气系统模态仿真与试验

2．1 建立有限元计算模型

如何建立排气系统准确合理的有限元模型一直是实际工程中的难点．考虑到排气系统尺寸较大、外形不规则，因此在建立有限元模型时需要适当的简化．作者在某客车排气系统CAD数模的基础上，采用Hypermesh软件建立有限元模型．对薄壁管型结构，采用壳单元模拟，连接法兰则采用体单元模拟，并充分考虑各主要部件正确的质量分布．所建立的有限元模型如图所示．

2．2 有限元模型分析与验证

作者首先对某客车排气系统模型在Hypermesh中进行了自由模态有限元分析，得出了仿真下的固有频率和振型．然后再对排气系统进行自由模态试验以验证模型的准确性，为后续的排气系统悬挂点的设计提供依据．

2．2．1 排气系统自由模态仿真分析

首先忽略排气歧管约束对排气系统振动的影响以及排气系统的吊挂件和支撑，进行了有限元模型的自由模态计算．求解出排气系统的固有振动特性，初步掌握系统固有频率及其振型等模态参数．本次分析采用Hypermesh中的optistruct模块进行模态分析．由于发动机激励频率范围为20～200Hz，因此计算0～200Hz范围模态，计算结果如表1所示．

表1列出了排气系统对应阶次的系统固有频率．由分析结果可见:前6阶为排气系统刚体模态，因而主要考虑第7～19阶模态．下面列出了部分模态振型结果图．

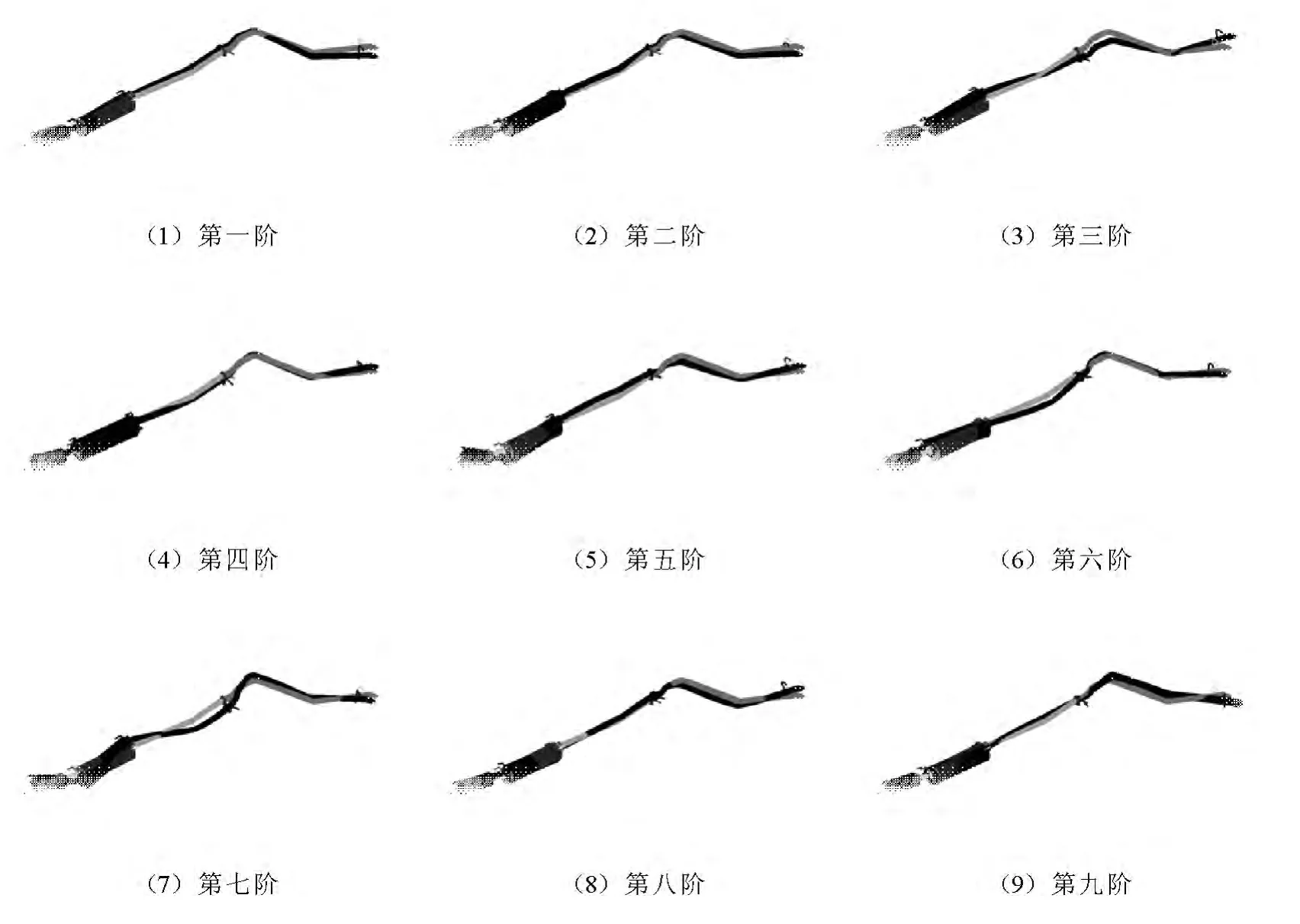
图2 排气系统自由模态部分振型

2．2．2 排气系统自由模态试验验证

2．2．2．1 试验对象

试验以如下图所示排气系统为试验对象，主要由波纹管、三元催化器、消声器、连接法兰、吊挂件及连接管组成．采用橡胶绳对排气系统进行悬吊，本次试验选用的绳子固有频率为1～2Hz，符合自由模态试验对试验边界条件的要求．

图3 排气系统实物图

2．2．2．2 试验方法简介

作者采用激振器接功率放大器后提供的随机猝发信号作为激励信号，并利用压电晶体加速度传感器拾取振动，之后采用LMS Test．lab软件进行模态分析处理软件．具体的测试系统如图4所示．试验悬吊方案如图5所示，测点和激励点如图6所示．

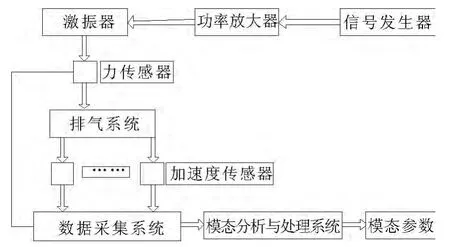
图4 示意图

具体过程如下:

(1)确定车辆坐标系．x轴负向为车辆前进方向，y轴正向为前进方向右侧，z轴正向为垂直向上，x，y，x 符合右手定则．

(2)确定支撑．根据自由模态试验要求的选取低于一阶自由频率10%原则，选取合适的橡皮绳于悬挂点处进行支撑．(见图5)．其评价方法:橡皮绳的最低阶频率(1．21Hz)低于排气系统第一阶固有频率的10%～20%．

(3)确定激励方案．选择激励点时需要考虑的地方:①为了保证采集的测点信号有较高的信噪比，避免模态遗漏，激励点位置应避开系统任一阶振型的节点;②激励点应选择刚度大且便于传递激励能量的位置．因排气系统较长，对其前后两端采用两点激励(见图6)，保证能量传递均匀，足以激起各测点振动．因激励点布置在曲面上，需要设定欧拉角．

(4)确定测点．测点选取时既要反映出排气系统的大致几何结构，也要避开任一振型节点位置．图中共布置22个测点(见图6)．排气系统存在较多曲面，在LMSTest．Lab Geometry中建立测点线框图时，需要考虑测点是否存在欧拉角．

(5)确定拾振方案．考虑排气系统多曲面结构特点，为更加精确获取各测点振动特性，需对每个测点测量x，y，z三个方向的振动加速度信号，一次测量一个方向，且加速度传感器换方向时，保证在同一位置．

(6)选择激励信号．为了满足输入信号不相关的要求，以及减少激振器之间的相互影响和解决系统的非线性近似线性问题，激振器发出猝发随机信号(burst random)作为激励信号．采用Hanning窗以减小泄露误差，并进行了30次线性平均，以减少测量的随机误差．

(7)选择试验频段．参考实际行驶中路面和发动机对排气管的激励频率范围，将试验频段定在0～100Hz．

图5 试验方案图

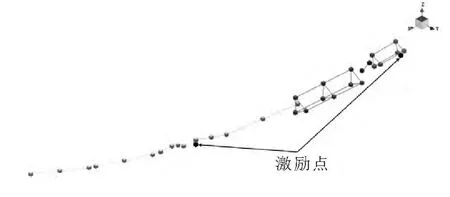
图6 激励点和测点线框图

2．2．3 数值计算与试验结果对比

通过上述试验的结果和仿真计算结果进行对比，可以判断出作者所建立的有限元模型是否合理．具体如下表所示．

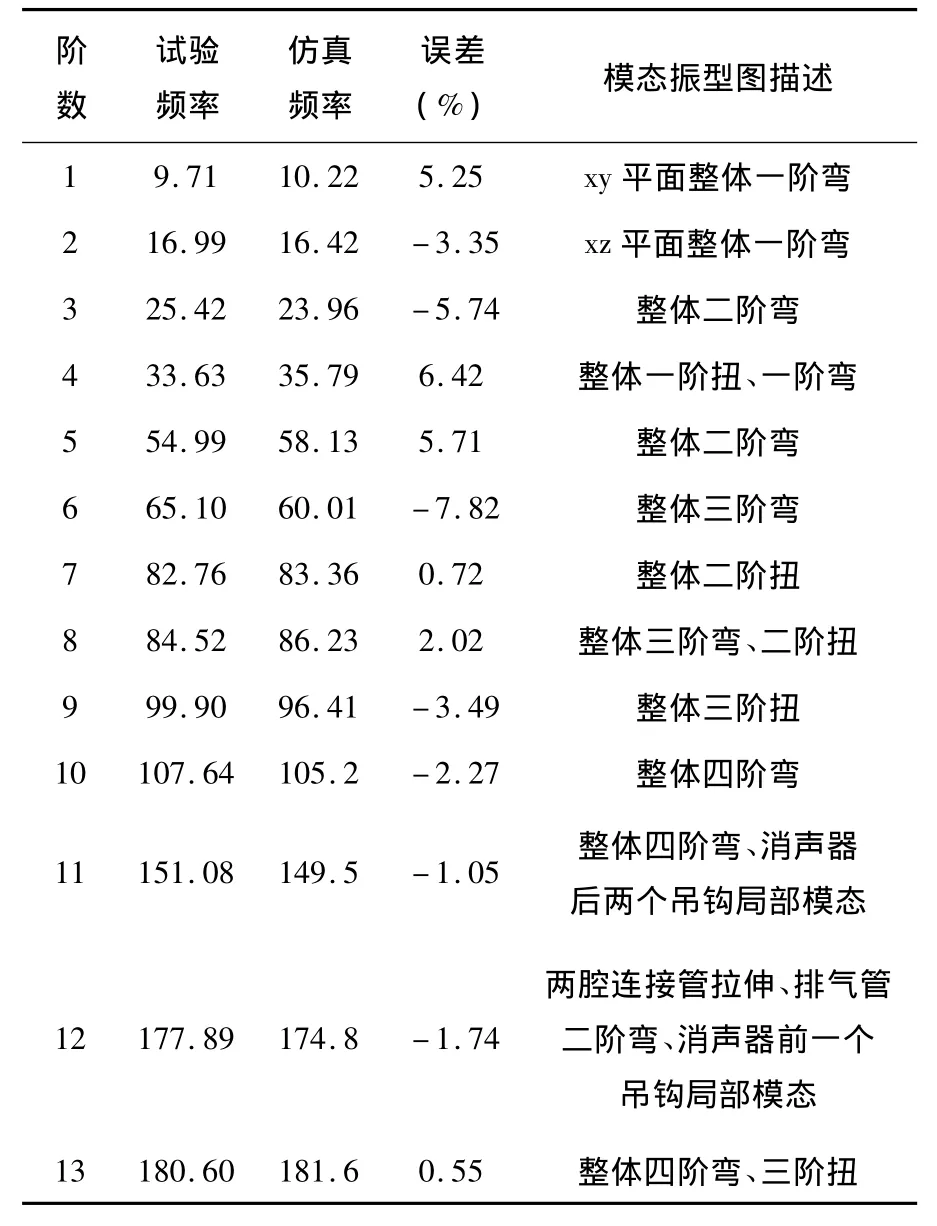
表2 仿真计算值与试验结果对比

从表2中可以看出，排气系统在自由模态下的计算模态和试验模态结果误差都小于10%，所以，所建立的排气系统模型是合理准确的，可以用于后续的仿真计算．

3 汽车排气系统悬挂位置优化

汽车排气系统的动力学分析一般仅考虑其冷端，即从排气系统前端法兰到尾管．其吊耳悬挂点原始位置如图7所示．

图7 排气系统吊耳位置

在排气系统中均列设置95个参考点，如图8所示．在上述计算自由模态时，将这些节点的位移在结果文件Pch中输出，然后对其位移向量加权累加．

图8 排气系统参考点位置

绘制节点的位移曲线，其中以位移向量的加权累加值为纵坐标，以吊耳潜在位置的参考点编号为横坐标，得出曲线如图9．

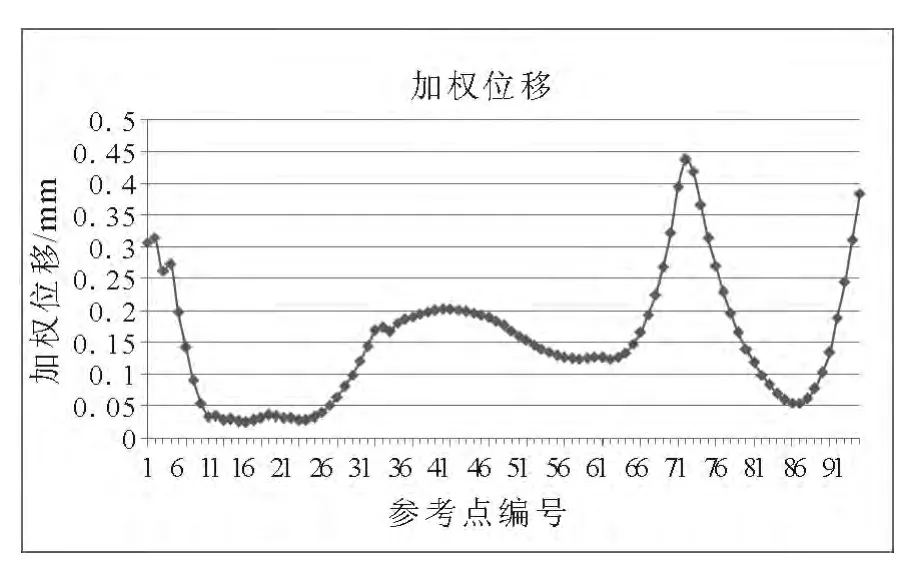
图9 自由模态参考点加权位移图

结合平均驱动自由度位移(ADDOFD)法的原理可知，ADDOFD的值最小的那些节点可以作为排气系统吊耳的较佳位置．也就是说图9曲线波谷或接近波谷的那些点应该是排气系统吊耳悬挂点，并且尽量不要选择位于波峰的点．参考排气系统的实际车身布置和系统的自身重量，做如下改进:

改进方案一:

1:吊耳1(第2参考点)移至第13参考点位置;

2:吊耳5(第92参考点点)移至第85参考点位置;

而吊耳2，3，4均处于曲线波谷或接近波谷的那些点，所以吊耳2、3、4的悬挂点不做修改．改进后的悬挂点布置位置如图10所示．

图10 吊耳悬挂点布置改进(一)

改进方案二:

1:吊耳1(第2参考点)移至第7参考点位置;

2:吊耳3(第31参考点点)移至第27参考点位置;

3:吊耳5(第92参考点点)移至第85参考点位置;

而吊耳2、4均处于曲线波谷或接近波谷的那些点，所以吊耳2、4的悬挂点不做修改．改进后的悬挂点布置位置如图11所示．

图11 吊耳悬挂点布置改进(二)

4 结语

本文利用有限元软件计算出排气系统的自由模态频率和振型，之后又对其进行了自由模态试验验证．在模型准确的前提下，再用有限元软件以平均驱动自由度位移方法，计算出相应点的位移响应值，以便最后选取合适的新悬挂位置．

在排气系统模型达到一定准确性的条件下，采用ADDOFD方法，从有限元仿真的角度出发，对排气系统的悬挂点提供理论依据，能加快开发开发速度，尤其是在排气系统的开发初期能起指导作用，能有效地降低开发费用和减少试验次数．

[1] 田育耕，刘江华，王岩松，徐振华．汽车排气系统振动模态分析及悬挂点优化[J]．辽宁工程技术大学学报(自然科学版)，2009，06:995 －998．

[2] 赵海澜，顾彦．汽车排气系统悬挂点优化[J]．计算机辅助工程，2006，S1:230 －231．

[3] 白化同，郭继忠，模态分析理论与实验，北京:北京理工大学出版社，2001．

[4] 马慰慈．某车排气消声系统悬置优化设计[D]．华中科技大学，2009．

[5] 郭荣，周鋐．某型轿车白车身试验模态分析及动态特性评价[J]．机械设计，2010，08:18－22．

[6] 徐献阳 ．车辆排气系统的振动模态分析及优化[D]．上海交通大学学报，2007．

[7] 徐献阳，李松波，张建武 ．某轿车排气系统振动特性仿真及优化[J]．设计与研究，2008，35(3):13 －14．

[8] 邢素芳，王现荣 ．发动机排气系统振动分析[J]．河北工业大学学报，2005，34(5):109－111．

[9] 杨万里，陈燕 ．乘用车排气系统模态分析数值模型研究[J]．三峡大学学报，2005(4):345－347．

[10] 田静．乘用车排气系统悬挂位置设计及隔振控制研究[D]．武汉理工大学，2011．

[11] 靳晓雄，吴颖江，彭为，高吉强，单莘．轿车白排气系统模态试验方法研究[J]．汽车技术，2009(5):39 －42．

[12] 徐献阳．车辆排气系统的振动模态分析及优化[D]．上海交通大学，2008．