基于Bang－bang 控制的无刷直流电机换相转矩波动抑制策略①

孙小飞， 周 苏，2， 王明强

(1．同济大学汽车学院，上海201804;2．同济大学中德学院，上海200092)

0 引言

无刷直流电机具有效率高、寿命长、结构简单、低噪声以及较好的转速－转矩特性等优点，因此在汽车、航空、家用电器等工业领域得到日益广泛的应用[1]．由于齿槽效应与非理想的方波电流输入，不可避免地引起输出转矩波动，限制了无刷直流电机在高精度伺服系统中的应用，寻求较好的转矩波动抑制策略也成为无刷直流电机目前的研究难题与热点．

针对齿槽转矩波动，文献[2]、[3]分别提出斜槽法和分数槽法对电机本体进行优化设计，得到了较好的齿槽转矩波动抑制效果．对于换相转矩波动，文献[4]提出采用重叠换相法，采用提前导通待换相绕组的方法，改变换相时总电流下降的现象，但是换相时刻难以确定，效果有限;文献[5]通过维持换相期间关断相电流下降斜率和开通相电流上升斜率相等来抑制换相转矩波动，效果较好，但该方法需要通过判断高、低速状态，给出不同的抑制策略，使得转矩脉动抑制过程复杂化;文献[6]采用扩张状态观测器观测电机转矩，结合跟踪微分器和非线性误差反馈规律实现对电机转矩波动的抑制．另外随着智能控制技术的发展，诸如模糊逻辑、神经网络、自抗扰技术等方法也在电机控制领域得到了广泛的应用．

本文通过研究换相过程中三相电流变化情况，提出基于Bang－bang控制的电压补偿策略，控制换相过程中关断相功率管合理地再导通，实现换相转矩波动的抑制．

图1 无刷直流电机及主驱动电路等效图

图2 换相电流、转矩波形

1 无刷直流电机换相过程分析

1．1 无刷直流电机数学模型

本文以常见的两两导通三相六状态Y接无刷直流电机为研究对象，建立数学模型前作出如下假设:(1)三相绕组完全对称、均匀分布;(2)不计电枢反应，气隙磁场分布近似认为是平顶宽度120°梯形波;(3)忽略齿槽效应、铁心饱和，不计涡流损耗和磁滞损耗[1]．

电机主驱动电路和等效电路如图1所示．图中L，M分别为定子绕组电感与绕组间互感，R为绕组等效电阻，Udc为直流母线电压，Uo为电机中性点，eA，eB，eC分别为 A，B，C 三相反电动势，iA，iB，iC为三相相电流．

由于采用Y接，三相电流满足

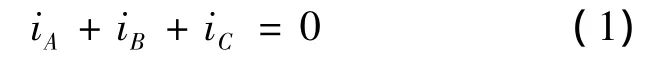
相电压方程，表示为矩阵形式

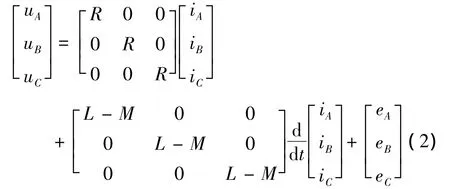
式中:uA，ub，uC为三相定子相电压．电磁转矩为

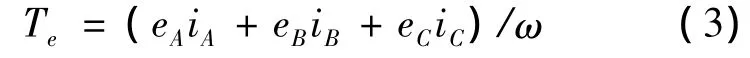
式中:Te为电机输出转矩，ω为转子的机械角速度．

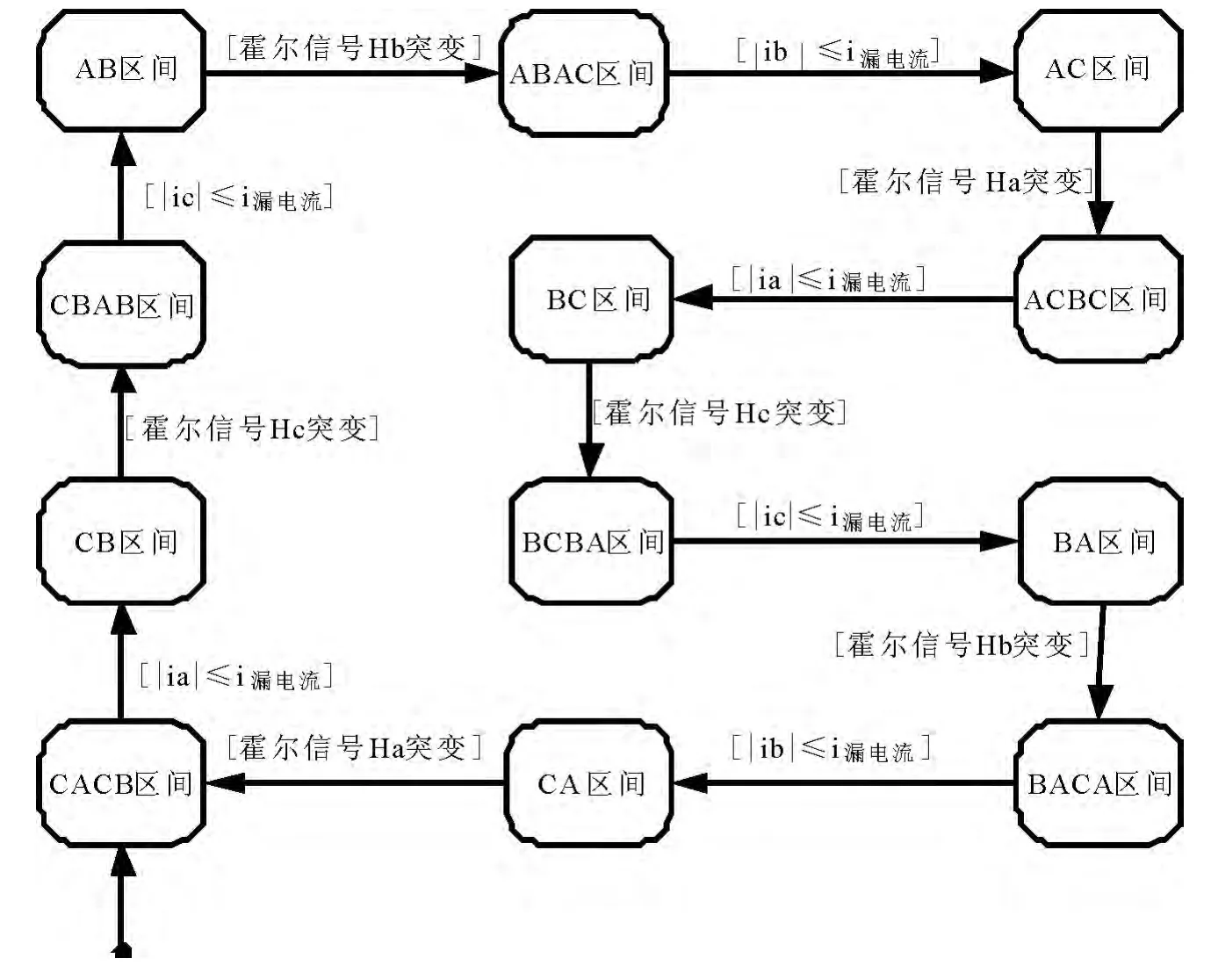
图3 电机工作区间判定

图4 换相过程功率管导通与关断示意图

1．2 换相转矩波动分析

由式(3)可以看出，在转速一定时，保持转矩恒定，即保持eAiA，eBiB，eCiC之和恒定，必须使电枢电流为理想方波且与反电势同相位．

以BC相导通切换为BA相导通为例，此时功率管VT2由导通切换为关断，VT4由关断切换为导通，VT3保持导通状态不变．实际过程中，由于二极管续流，C相电流不会立即跳变为0，A相电流也不会立即跳变为相电流I．文献[7]指出在不同转速下，C相电流下降速率与A相电流上升速率不一致，且换相过程持续时间不同，根据式(1)、式(3)，输出转矩会有明显波动，如图2所示．

文献[8]通过计算最佳换相点矫正电机换相时刻，以调整换相期间电流上升 /下降的速率，减小转矩波动，但由于换相过程电流变化为非线性过程，同时电机参数在工作过程中时变、漂移的影响，最佳换相点往往难以确定，且对转矩波动抑制效果有限．

2 基于Bang－bang控制的转矩控制

2．1 转矩波动抑制策略

上文分析可知，由于换相过程二极管续流，电机输出转矩跌落，如果对电机进行适当的电压补偿，可以抑制转矩跌落，达到抑制转矩波动的目的．电压补偿通常通过控制关断相再导通来实现，关键在于导通时间的确定，多数的研究策略主要是控制提前换相，不能根据转矩波动情况实时调整．本文拟通过观测转矩偏差实时控制关断相功率管再导通来实现电压补偿，还是以BC相导通切换为BA相导通为例，换相期间功率管VT2状态在0与1之间切换．

Bang－bang控制作为一种时间最优控制，它的控制函数总是取在容许控制的边界上，或者取最大，或者取最小，仅仅在这两个边界值上进行切换，作用相当于一个继电器，在系统有偏差时，能最大程度地加大系统的控制力度，提高了系统的快速性[9]．鉴于此，对 VT2采用 Bang － bang控制．

2．2 Bang－bang控制器设计

2．2．1 控制指标的引入

控制指标需反映转矩波动的大小，由之前的分析可知，换相时电机输出转矩Te偏离期望转矩Tr，由此引入转矩跟踪效果指标，即转矩随动误差RT:

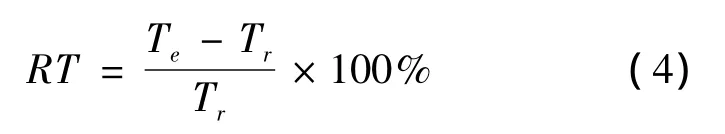
2．2．2 换相区间的判定

由于需要在换相区间进行控制，必须准确判断电机运行状态，因此将电机分为12个工作区间，即六个正常运行区间与六个换相区间[10]．

首先，根据霍尔位置信号确定当前电机所处的60°工作区间;其次，比较三相绕组相电流测量值，如果绝对值均大于功率管漏电流，则此时系统处于换相区间，否则处于非换相区间[11]．由于无刷直流电机工作时在各区间切换有一定顺序，可以采用事件触发Stage，更利于系统工作区间的确定，如图3所示．图中AB表示只有A、B两相导通的工作区间，CBAB表示由CB切换为AB的换相区间，其它区间依次类推．

2．2．3 Bang － bang控制过程

仍以BCBA换相区间为例，介绍对关断相C相的Bang－bang控制．具体是:当电机转矩随动误差RT低于下限值RTmin时，为阻止电机转矩进一步跌落，导通VT2，此后，电机转矩上扬，直至电机转矩的随动误差RT高于上限值RTmax，关闭VT2，以防止电机转矩进一步冲高，如此反复不止，通过对关断相合理地再导通，使电机转矩随动误差RT保持在范围[RTmin，RTmax]．其中，RTmin和 RTmax需合理选取，主要取决于续流区间工作长度．其他换相区间的Bang－bang控制方法如表1，换相区间无刷直流电机各功率管的导通与关断如图4所示．

表1 关断相断电势的Bang－bang控制

2．2．4 控制系统设计

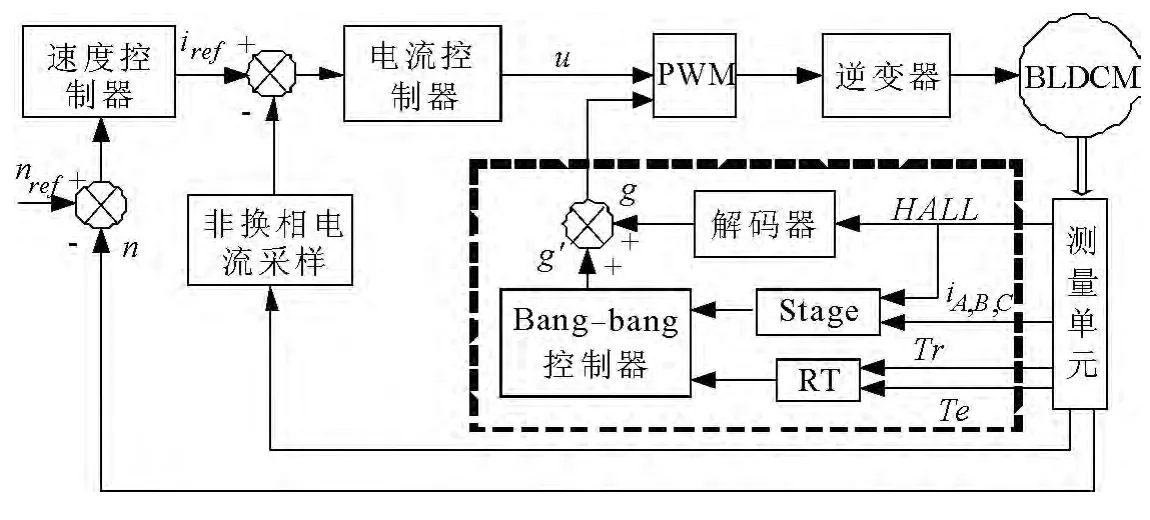
图5 控制系统结构框图

换相期间采用Bang－bang控制进行电压补偿，非换相期间用PWM控制，控制系统框架设计如图5．系统由外部输入参考转速nref与参考转矩Tr(即负载转矩TL)，换相过程中关断相功率管的再导通通过Bang－bang控制实现，与传感器位置信号解码后的功率管控制信号g叠加后传递给PWM模块，速度控制器与电流控制器采用经典的PI控制，经处理后的电压控制信号u与三角载波比较后控制功率管的开关频率．

3 仿真实验

根据控制框图5，在Matlab/Simulink环境下对无刷直流电机控制系统进行建模与仿真实验．

电机模型参数为:电源电压Us=100V，转子转动惯量J=1．78kgm2，阻尼系数f=0．2387N·m·s/rad，极对数p=1，定子绕阻R=0．2268Ω，定子绕组自感L=0．0038H，互感M= －0．0014H，反电动势常数ke=1．62V·s/rad．

仿真参数设置为:直流母线电压Udc=400V，额定转速n=1500r/min，负载转矩TL=50N·m．转矩随动误差控制阈值为[－1%，－0．1%]．

图6 换相过程三相电流波形

图6a，6b分别为Bang－bang控制前后三相电流波形，对比换相过程中两者电流变化趋势，采用本文的电压补偿策略后处于换相状态的A，C两相电流上升/下降速率基本保持一致．

图7a，7b分别是Bang－bang控制前后转矩输出波形，后者转矩波动明显减小，说明Bang－bang控制对换相转矩波动的抑制效果显著．

图7 换相过程转矩波形

图8是无刷直流电机典型工况模拟，电机工作在恒转矩区间与恒功率区间的转矩－转速曲线[11]，转矩跟踪误差保持在较小，不受转速高低的影响，与理论分析一致．

图8 无刷直流电机转矩跟随曲线

4 结论

本文分析了电机换相转矩波动的原因，针对换相转矩波动，提出基于Bang－bang控制的电压补偿策略，经过仿真验证，将转矩跟随误差控制在1%以内，方法简单有效，为进一步实际应用提供了理论依据．

[1] 夏长亮．无刷直流电机控制系统[M]．北京:科学出版社，2009．

[2] 张晓宇，王晓远．减少齿槽转矩的无刷直流电机优化设计[J]．微电机，2013，46(1):24 －27．

[3] 张科，史祥翠．永磁无刷直流电机齿槽转矩削弱方法[J]．煤矿电机，2009，6:37 －39．

[4] Murai Y，Kawase Y Ohashi K．Torque Ripple Improvement for Brushless DC Miniature Motors[J]．IEEE Industry Applications Society Annual Meeting，1987，25(3):441－450．

[5] Joong Ho Song，Ick Choy．Commutation Torque Ripplereduction in Brushless DC Motor Drives Using a SingleDC Current Sensor[J]．IEEE Transactions on PowerElectronics，2004，19(2):312－319．

[6] 夏长亮，俞卫，李志强．永磁无刷直流电机转矩波动的自抗扰控制[J]．中国电机工程学报，2006，26(24):137－142．

[7] Carlson R，Lajoie M M，Fagundes J C．Analysis of Torque Ripple Due to Phase Commutation in Brushless DC Machines[J]．IEEE Transactions on Industry Applications，1992，28(3):632－638．

[8] 罗宏浩，吴峻，赵宏涛，等．永磁无刷直流电机换相控制研究[J]．中国电机工程学报，2008，28(24):108 －112．

[9] 郭俊铭．Bang－bang控制在随动系统中的应用[J]．伺服技术与系统，2007:38－40．

[10] 李鲲鹏，胡虔生，黄允凯．计及绕组电感的永磁无刷直流电动机电路模型及其分析[J]．中国电机工程学报，2004，24(1):76－80．

[11] 周苏，王明强，陈凤祥．基于反馈线性化的车用无刷直流电机转矩随动控制[J]．武汉科技大学学报，2012，35(5):391－398．