针对高速列车头车外形设计的风洞侧风试验模型选取方法①

张曙辉， 杨志刚， 陈 羽

(同济大学上海地面交通工具风洞中心，上海201804)

高速列车在强侧风作用下，由侧风效应所引起的列车失稳和倾覆事故在世界各地时有发生，侧风已经成为影响列车安全运行的重要因素之一[1]．大量研究[2～10]指出，在各个风向角情况下，列车头车的侧向力系数和倾覆力矩系数大于其他位置车辆，发生脱轨倾覆的可能性最大，良好的气动外形在高速列车安全行驶方面起着关键作用．

由于雷诺数对高速列车风洞试验的影响，需要尽可能采用大尺寸的缩比模型，来减小雷诺数对气动力的影响，提高风洞试验中气动力测量的准确性，同时减小模型几何相似性的影响[11]．高速列车是一个细长体，风洞侧风试验模型的阻塞比要远远小于5%，关键制约因素归结为列车模型的长度[12]．因此，对风洞中侧风试验的更短列车模型的选取进行研究具有重要意义．

本文通过计算流体力学的方法，对3车、2车、1．5 车(头车 +0．5 尾车带转向架)、1．5 车(头车 +0．5尾车不带转向架)和1．2车(头车+0．2尾车)等5种模型的侧风气动特性进行仿真计算，研究了不同侧风情况下列车模型的气动力和流场结构，提供了可以用于风洞侧风试验的高速列车模型．

1 数值模型

1．1 不同侧风试验模型

高速列车模型采用文献[13]中提到的方法进行参数化建模．为了与目前我国高速列车风洞试验模型的尺寸保持一致，使得数值计算具有参考价值，本文数值计算采用1:8的缩比模型，模型头尾车流线段长度均为0．75m，总长度分别为9．375m，6．25m，4．6875m，4．6875m 和 3．75m 的五种模型，分别记为 A，B，C，D 和 E，见图1所示．其中，模型A为3车编组(头车+中间车+尾车)，模型B为2车编组(头车+尾车)，模型C、D均为1．5车编组(头车+0．5尾车)，区别在于模型C尾车带一个转向架，而D尾车不带转向架，模型E为1．2车编组(头车+0．2尾车)．模型A和B的头尾车外形相同，模型C、D和E的尾车采用文献[14]的方法进行建模．

1．2 计算区域及网格划分

计算域分为来流区和尾流区，根据绕流流场的特性，尾流区取较大值，在列车后侧和背风侧取较大值，本文计算域为:长8L，宽30W，高13H的长方体，其中L为单节车长，W为车宽，H为车高．如图2所示．

在本次计算中，使用了混合型网格进行空间离散，在近车体区域使用三棱柱和四面体网格，而在距离车体较远的区域采用的是六面体网格．为了更准确地计算车体表面摩擦阻力，在车体、转向架和轨道表面生成边界层网格，边界层第一层网格厚度为1mm．A～E模型的计算网格数分别为700万，600万，513万，490万和470万．

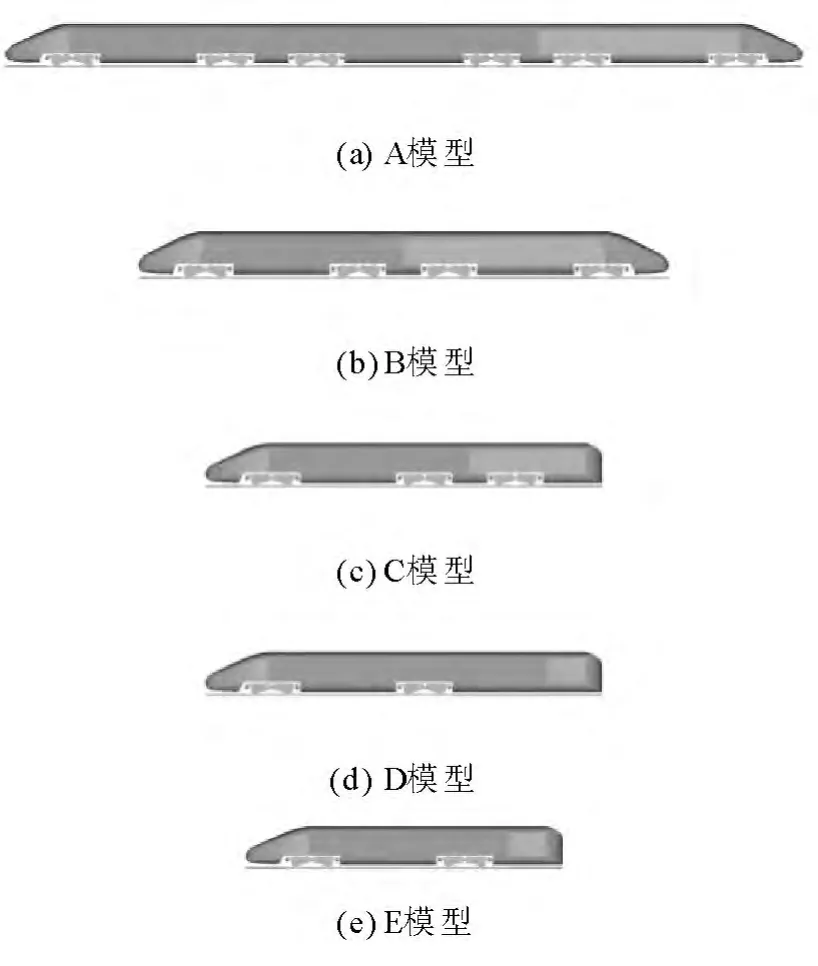
图1 不同列车模型示意图

图2 计算域及速度的表示

1．3 条件设置和计算工况

选用基于有限体积法的商用CFD软件Fluent进行求解．湍流模型采用Realizable κ－ε两方程模型，并选用SIMPLE压力修正法．在边界条件的设置上，地面设置为移动地面，速度大小和方向均与来流速度一致，以模拟列车和地面之间的相对运动;顶部设为对称边界条件;列车车身、转向架和轨道设为无滑移速度的固壁边界条件;主流方向入口和侧向入口均设置为速度入口，列车正前方均匀来流与列车运行速度Vt等值反向，侧风速度为Vcw，二者的合成速度为V，合成速度V与来流方向的夹角定义为合成风向角，参见图2;主流方向出口和侧向出口均设为压力出口，静压值为零，即全场参考压力面．通过上述计算方法，对每个模型分别计算了以下4种工况，如表1所示．

表1 计算工况

2 计算结果和分析

在有侧风工况下，不仅关心列车阻力，列车的行车安全性更是人们关注的一个重点．一般用侧向力系数、升力系数和倾覆力矩系数来描述列车的侧风稳定性．头车的侧向力系数、升力系数及倾覆力矩系数与高速列车在大风下的行驶稳定性密切相关，阻力系数与列车动力匹配密切相关，以上4个系数是高速列车风洞侧风模型试验评价的最主要参数．各空气动力系数定义方式如下:

阻力系数

升力系数

侧向力系数

倾覆力矩系数

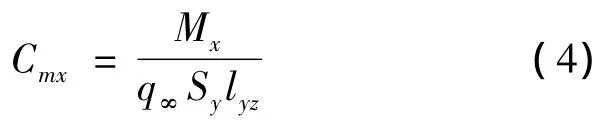
式中，Fx，Fy和Fz分别为列车受到的阻力、侧向力和升力，N;Mx为作用于列车的倾覆力矩，N·m;q∞为来流动压，Pa;ρ为来流空气的密度，取1．225kg·m－3;V∞为特征速度，本文取为各工况的合成速度m·s－1，Sx，Sy和Sz分别为列车的横截面积、侧向投影面积和水平投影面积，m2;lyz为列车的高度，m．

2．1 不同试验模型对头车气动力的影响

不同侧向风速下，不同试验模型对头车气动力的影响如图3所示．从图中可以看出，相同侧风条件下，不同试验模型头车的阻力系数、升力系数、侧向力系数和倾覆力矩系数存在差别，但是差异不大．针对上述计算结果给出的解释是:无论选取何种模型，气流都是从列车头部开始沿着列车流动的，在列车头部模型不变的情况下，相同车速和侧风条件下，列车的外部绕流流场结构相似．

考虑到高速列车在侧风环境中的安全行驶性能，在风洞侧风试验中，我们更多关注的是侧向力系数和倾覆力矩系数这两个物理量．从图3(c)(d)可以看出，在每个侧向风速下，模型A，B，C和E的侧向力系数和倾覆力矩都是依次递减的，且侧向风速越大减少量越大．侧向风速为20m/s时，侧向力系数降低了3．24%，倾覆力矩系数降低了3．42%．从模型A到模型E，侧风试验模型的编组长度是逐渐减小的，头车后面的中间车或尾车的底部结构不同，流动的发展因模型长度和底部结构的不同而出现差异．因此，不同模型的气动力系数各不相同．

图3 不同列车模型对头车气动力的影响

经过以上分析可知，采用模型E即1．2车模型代替三车模型进行高速列车的风洞侧风试验，并通过分析头车的气动力特性来评估整车的气动安全性是可行的．

2．2 头车各部分对气动力系数的贡献情况

为了研究不同试验模型对列车头车气动力的影响及其位置，本文将头车沿列车行驶方向划分成4个区域，如图4所示．其中，区域Ⅰ为头车流线段，区域Ⅱ、Ⅲ和Ⅳ为头车车身段沿流动方向的不同位置区域．

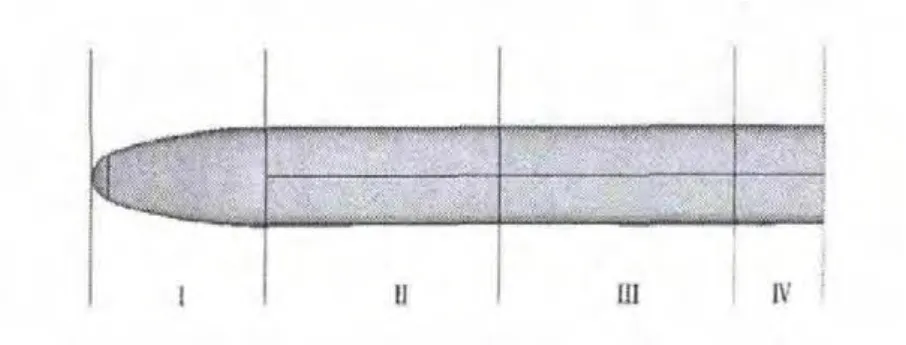
图4 头车区域划分情况

通过计算流体力学的方法，可以得到不同区域所受到的气动力及其对总气动力的贡献情况．基于侧风安全性的考量，本节的关注点依然是侧向力系和倾覆力矩系数．特定的列车速度(本文为200km/h)，对于不同的侧向风速，合成风向角即偏航角不同．研究发现，从小偏航角工况(侧向风速5m/s)到大偏航角工况(侧向风速20m/s)，不同区域对头车气动力的贡献情况是有区别的，如图5所示．

图5 头车不同区域的受力情况

在小偏航角工况下，区域Ⅲ和Ⅳ受到的侧向力和倾覆力矩特别是区域Ⅳ所占的比重很小，而对于大偏航角工况，头车后半部占总量的比重增加．从图5(a)和(b)可以看出:小偏航角工况下，区域Ⅰ、Ⅱ和Ⅲ受到的侧向力和倾覆力矩在不同模型之间规律不明显;区域Ⅳ受到的侧向力从模型A到E减小了70．58%，倾覆力矩减小了57．11%．从图5(c)和(d)可以看出:大偏航角工况下，区域Ⅰ和Ⅱ的侧向力和倾覆力矩与模型无关;对于侧向力系数，从模型A到E，区域Ⅲ减小了8．38%，区域Ⅳ减小了12．35%;对于倾覆力矩系数，从模型A到E，区域Ⅲ减小了8．49%，区域Ⅳ减小了11．45%．综合考虑不同区域气动力的变化量及贡献比重，可得出结论:各个模型的头车侧风性能存在差异的原因在于区域Ⅲ和Ⅳ受到的侧向力和倾覆力矩不同，且主要差异来源于区域Ⅳ．

2．3 不同侧风试验模型流场分析

列车的外部绕流流场直接影响列车各个部分所受到的气动力，为了研究同一工况不同模型受力不同的原因，需要分析不同模型在不同工况下的外部绕流流场．

研究发现，大、小偏航角工况下的流场结构存在一定的差异．小偏航角工况下(车速200km/h，侧风5m/s)头车末端的背风侧存在一个附着于壁面且顺时针方向旋转的小尺度分离涡，涡核位置在竖直方向上位于半车高偏上的位置;大偏航角工况下(车速200km/h，侧风20m/s)，相同的位置有两个旋转方向相反的分离涡存在，这两个分离涡的尺寸和涡核位置对于不同的模型而言存在差别，影响压力分布．由于篇幅所限，本文只给出大偏航角工况下头车末端横截面的流线图，如图6所示．

从图6中可以看出，模型A、B和C横截面上的流线图基本无差别，模型D和E的横截面上的流线图相似，但明显区别于前三者．原因在于，此处的流场结构受前方发展而来的分离涡、尾涡和底部结构的影响．前三个模型在此截面前后的底部位置均有一个转向架，而模型D和E在此截面后没有转向架．

通过特征向量法确定各模型涡核位置，涡核寻找基于临界点理论展开．以大偏航角工况为例，从图6(a)～(e)可看出，涡核位置随着模型长度的缩短向车体背风侧靠近，涡核与列车纵向对称截面的距离从2．59B减小到2．52B，横向距离降低2．7%．负压区向着车体移动，影响头车末端的侧向气动性能．

为了进一步探索能否采用更短的模型进行高速列车风洞侧风试验，需对比分析模型A和E车身表面的压力分布云图．经上文分析得知，列车头车的前三个区域几乎无差异，下文仅对部分区域的表面压力分布云图进行重点阐述．分析头车区域Ⅳ和紧邻其后0．2倍车长区域在大、小偏航角工况下的压力分布，如图7所示．可以看出，模型E区域Ⅳ迎风侧的压力分布明显异于模型A，迎风侧和背风侧的压力差决定了侧向力的大小．表面压力分布受前方来流的发展运动、底部结构和尾部结构这三者的共同作用，观察模型E的区域Ⅳ和尾车的表面压力分布，可以发现尾部负压区影响到前面区域的压力分布和流场结构，影响范围最大为0．16倍车长，因此不建议使用更短的模型．

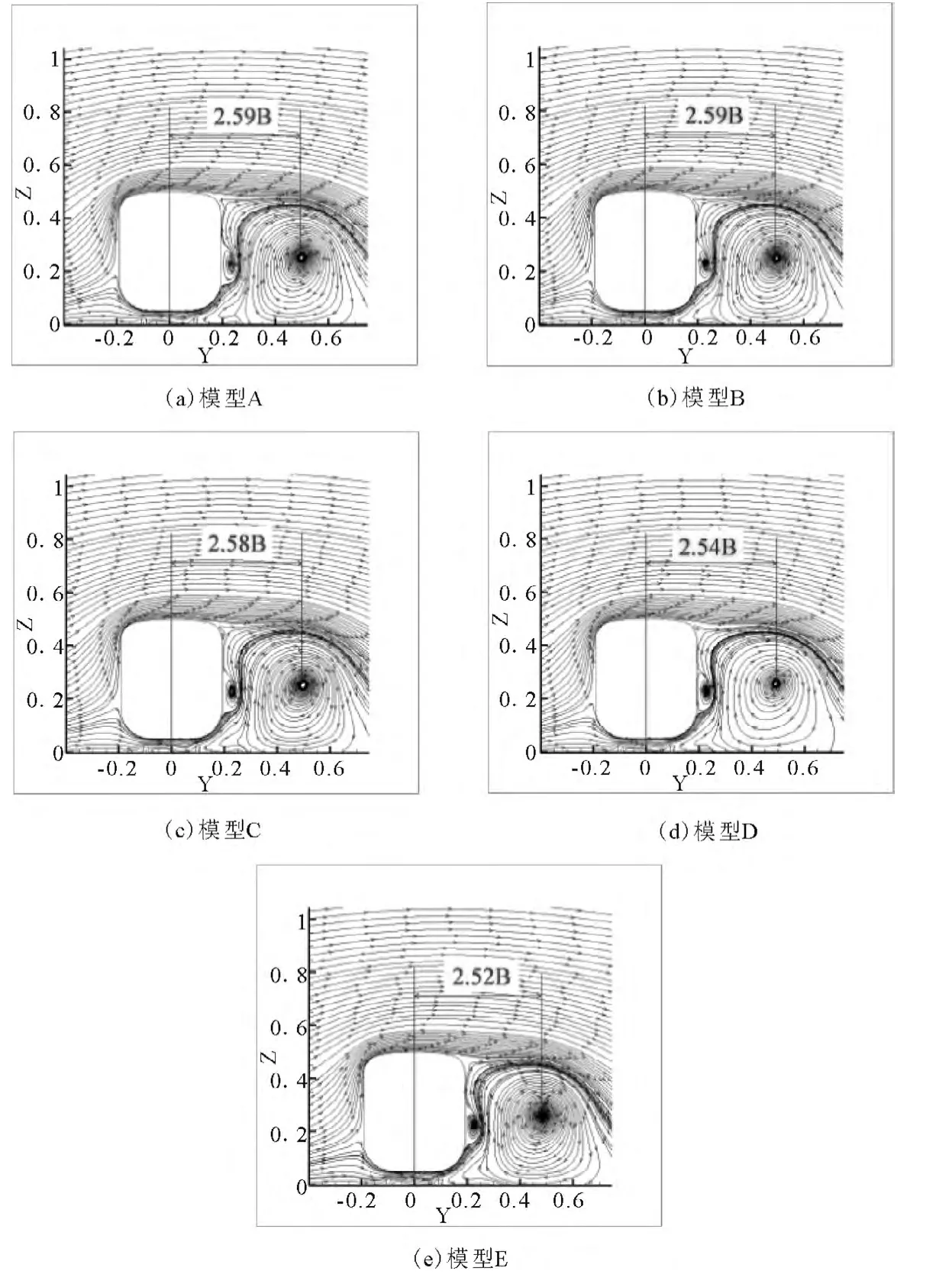
图6 头车末端横截面流线图(图中B表示半车宽)

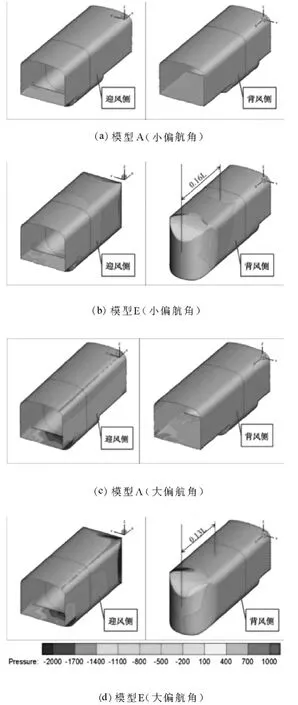
图7 列车表面迎风侧和背风侧的压力分布云图

3 结论

通过数值模拟计算的方法，研究了侧风工况下，不同侧风试验模型对高速列车气动特性的影响规律，得到了以下结论:

(1)相同侧向风速下，高速列车风洞侧风试验模型对头车的阻力系数、升力系数、侧向力系数和倾覆力矩系数影响不大，可以采用更短编组长度的列车模型E(1．2车模型)代替模型A(三车联挂模型)，对列车的侧风稳定性进行评估．

(2)相同的列车运行速度和侧向风速下，气流都是从列车前端绕相同的头车沿列车流动的，外部绕流流场结构和列车表面压力分布的差异不大．因此，可以采用1．2车模型代替三车模型进行风洞侧风试验，但考虑到尾车结构对头车末端区域Ⅳ的流场和压力分布的干扰，不建议采用更短的模型．

[1] Andersson E，Haggstrom J，Sima M．Assessment of Train － Overturning Risk Due to Strong Cross － Winds[J]．Proceedings of the Institution of Mechanical Engineers Part F－Journal of Rail and Rapid Transit，2004，218(3):213 －223．

[2] 毛军，郗艳红，杨国伟．侧风风场特征对高速列车气动性能作用的研究[J]．铁道学报，2011，33(4):22－30．

[3] 任尊松，徐宇公，王璐雷，等．强侧风对高速列车运行安全性影响研究[J]．铁道学报，2006，28(6):46－50．

[4] 田红旗，高广军．270km*h－1高速列车气动力性能研究[J]．中国铁道科学，2003，24(2):14 －18．

[5] 张在中，周丹．不同头部外形高速列车气动性能风洞试验研究[J]．中南大学学报(自然科学版)，2013，44(6):2603－2608．

[6] 黄志祥，陈立，蒋科林．高速列车模型编组长度和风挡结构对气动阻力的影响[J]．实验流体力学，2012，26(5):36－41．

[7] 马静，贾青，杨志刚．基于数值计算的高速列车气动阻力风洞试验缩比模型选取方法[J]．计算机辅助工程，2007，16(3):110－118．

[8] 毛军，郗艳红，杨国伟．列车编成辆数对高速列车横风气动特性影响的数值研究[J]．中国铁道科学，2012，33(1):78－85．

[9] 郗艳红，毛军，李明高，等．高速列车侧风效应的数值模拟[J]．北京交通大学学报，2010，34(1):14－19．

[10] 黄志祥，陈立，蒋科林．高速列车空气动力学特性的风洞试验研究[J]．铁道车辆，2011，49(12):1－5．

[11] Backer C J，Brockie N J．Wind Tunnel Tests to Obtain Aerodynamic Drag Coefficients:Reynolds Number and Ground Simulation Effects．Journal of Wind Engineering and Industrial Aerodynamics，1991，38:23 －28．

[12] Chen Yu，Yang Zhigang，Wang Weijie，Gao Zhe．Effect of Length on Aerodynamics of High Speed Train Models[C]．The Sixth International Conference on Nonlinear Mechanics(ICNM－VI)，2013:468－472．

[13] 张伟．高速列车外形参数化设计[D]．成都:西南交通大学，1999．

[14] Railway applications－Aerodynamics－Part 6:Requirements and Test Procedures for Cross Wind Assessment．FprEN 14067－6:2009．