借助几何直观教学 积累数学活动经验

王卫东　潘淑芬

数学活动经验是《数学课程标准》（2011年版）提出的核心概念之一。重庆师范大学仲秀英教授认为：“数学活动经验可以理解为学生从经历的数学活动过程中对活动的感受、体验、感悟，以及由此获得的数学知识、技能、情感与观念等组成的有机组合性经验。”其实，就经验本身而言，就是一种感受、体验、感悟，具有较强的内隐性，所以在教学过程中，教者有时难以把握、调控与评价。为此，我们有必要借助几何直观进行教学，使内隐的数学活动经验得以外显，进而再根据这些外显的“证据”，对数学活动经验进行具化、调控与提升，从而实现数学活动经验的有效积累。

一、借助几何直观具化数学活动经验

数学学习离不开直观形象的思维，积累数学活动经验的过程更是如此。借助几何直观教学，我们可以把复杂的问题变得简明、形象，与此同时，也可以将学生在学习过程中的感受、体验与感悟变得具体、直观。从而在数与形、图与形的沟通与联系中，让那些看似虚无飘渺的数学活动经验变得看得见、摸得着了。

片段一：在教学《倍数和因数》时，教者开展了这样的教学活动。

师：你能找出12的因数吗？请在数轴上表示出来。

师生交流，在数轴上标出12的因数。

师：同学们，仔细观察数轴。看到这些因数，你想到了什么？

生1：我发现12最小的因数是1，最大的因数是12，也就是它本身。

生2：我认为12的因数可以成双成对地找出来，如1、12，2、6，3、4。

生3：对，而且每组的两个因数还越来越接近。

……

生：老师，我有一个疑问：是不是所有的数，因数的个数都是偶数个呢？

师：你的想法很有价值，那到底对不对呢？我们不妨举些例子来试一试。

思考：很难想象，一个数的因数能与几何直观图产生什么样的“化学反应”，然而，在上述教学环节中，教者却巧妙地借助数轴这个形象直观的载体，将学生的数学活动经验进行了定格与凝结。通过数轴上点与点之间的关系描述，教者简单有效地捕获到了学生思维发展的轨迹：最大因数与最小因数的特点、因数的分布特征、寻找因数的方法、因数个数的规律探究……更为重要的是，借助几何直观的“具化”作用，学生在思维的激烈碰撞过程中，从模糊到明晰、从简单到复杂、从模仿到内化，他们慢慢地积累了发现问题的经验、思考问题的经验以及解决问题的经验。

二、借助几何直观调控数学活动经验

积累基本数学活动经验的过程也是数学活动经验的内涵之一。一般来说，积累基本数学活动经验的过程大致需要经过经历、内化、概括、迁移的过程。在这样的过程中，我们需要借助几何直观来发挥教师的主导作用，适时对积累数学活动经验的过程加以调控。

片段二：在教学《解决问题的策略——转化》时，教者开展了这样的教学活动。

师：刚才大家用通分的方法计算出了+++的结果，这里的通分，其实就是一种转化的策略。除了通分以外，你还有其他方法吗？（学生思考）

师：观察这幅图（图1），想一想，它与算式之间有什么样的联系？（学生讨论）

师：现在你有什么新想法？

生：我想这样计算：1-=，因为阴影面积=总面积-空白面积。

师：你们认为呢？

生：我认为很巧妙！有了这幅图，可以把加法转化成减法来计算。

生：是的，用图形来表示算式，很好理解。

师：既然借助图形来解决问题这么好，那是不是在任何情况下都能使用它呢？

（学生思考、讨论）

生：我认为把算式转化为图形也有一定的局限性。大家看，这里阴影部分的面积之间都有着2倍的关系：是的2倍，是的2倍……

师：那是不是说，只要相邻加数是两倍的关系，我们就能借助这样的图去思考呢？

生1：是的，比如说++++（学生边说边画图）就可以转化为1-。

生：我也想了个算式：+++++…+=1-。

师：有道理。观察下面的图（图2），看看有什么新发现？

生：这里的加法虽然不是从开始加起的，但相邻加数之间仍然有着两倍的关系，我认为可以这样转化：1--=。

师：聪明！同学们受到他的启发，现在看到这幅图（图3），你又有什么想法呢？

生1：我发现这样的转化方法还能用在整数的加法上，只要相邻加数存在着两倍的关系。

生：是的，这里的转化策略不仅适用于整数、分数的计算，小数也可以。

思考：在上面的教学片段中，教者借助几何直观开展了三次教学调控。在第一次调控中，教者引导学生将算式+++与图1相联系，使他们认识到这类算式中加数的特点，积累了数形结合的思考经验，感悟了“转化策略也有局限”的探究经验。在第二次调控中，教者借助图2，对+++进行了变式与拓展，帮助学生积累了分析比较、灵活运用的经验。在第三次调控中，教者再次借助图3引导学生将数学活动经验进行了正向迁移，帮助他们积累了猜想验证、归纳推理的经验。

从图1、图2到图3，在教师的适时调控之下，学生经历了不同层次的经验积累，从知识经验、技能经验，再到数学思想方法的经验，他们在质疑与反思中进行了自我内化与建构。

三、借助几何直观提升数学活动经验

学生需要掌握什么样的数学活动经验？是知识的经验、技能的经验，还是关于数学思想方法的经验？毫无疑问，这些数学活动经验我们都需要，数学教学离不开知识，在知识的学习过程中可以培养学生的能力，感悟数学思想方法。多年以后，知识可能会遗忘，技能可能会生疏，数学思想方法也可能会淡去，既然如此，那什么样的数学活动经验才是学生受用一生的经验呢？

片段三：在教学《乘法分配律》时，教者开展了这样的教学活动。

1.师：你能用自己的语言来说说什么是乘法分配律吗？（学生互相交流）

师：大家已经知道了乘法分配律，那你能用更简单的方法表示出来吗？

学生尝试用不同的方法表示：（我+爱）×学=我×学+爱×学；（△+□）×○=△×○+□×○；（a+b）×c=a×c+b×c……

2.出示：

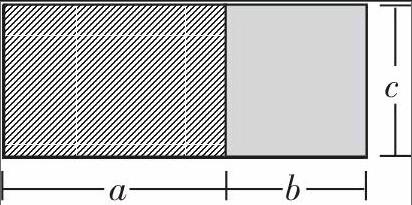
师：你能用两种不同的方法表示出这个图形的面积吗？

生：（a+b）×c或者a×c+b×c。

师：观察这幅图和两个算式，你想到了什么？

生：（a+b）×c=a×c+b×c。

生：哦，这就是乘法分配律！

师：是的，这幅图就蕴含了乘法分配律，而乘法分配律也可以用这幅图来表示。大家看，同样是乘法分配律，从不同的角度来审视，却有着不一样的精彩。其实，生活中也是如此，我们要学会从不同的角度来分析问题、解决问题，只有这样，我们的认识才会更全面，思考才会更有价值。

思考：在上面的教学环节中，为了阐述乘法分配律，教者设计了三个教学阶段。先用语言描述规律，然后用汉字、图形、符号来表示规律，最后用求长方形面积的图形来表示规律。这其中，教者巧妙地借助几何直观将乘法分配律与图形进行了有机结合，实现了乘法分配律的表达层次由低级到高级，表达形式由单一到多元的经验积累。与此同时，教者还引导学生从知识的文本中跳出来，引领他们用数学的眼光来观察世界，认识世界——“我们要学会从不同的角度来分析问题、解决问题，只有这样，我们的认识才会更全面，思考才会更有价值！

数学是一种智慧，成尚荣教授认为：“数学教育要‘为智慧的生长而教。”因此，数学活动的经验不能禁锢于知识与技能的经验，也不能止步于思想与方法的经验，我们理应帮助学生造就智慧人生的经验。在上述三个教学片段中，教师引导学生跳出了数学知识的文本经验，跨过了数学思想方法的经验，感悟了人生智慧的经验。从知识走进方法，从思想走近智慧，借助几何直观，数学活动经验的积累由此得到了质的提升与飞跃。