基于探头声场特性的钢轨超声检测研究*

张书增，杨岳，刘希玲，李雄兵，胡宏伟

(1.中南大学CAD/CAM研究所，湖南长沙 410075;2.长沙理工大学汽车与机械工程学院，湖南长沙 410114)

钢轨的质量是保证铁路运行安全的重要因素之一，而钢轨在生产及使用过程中，不可避免的会出现各种缺陷［1］。存在钢轨内的缺陷类型较多，而且在钢轨的轨头、轨腰和轨底均有分布，如不能及时有效地检出缺陷而使得其逐步扩大，将给铁路运行安全带来重大隐患［2－3］。因此，必须对钢轨进行周期性检测，以避免铁路事故的发生。检测钢轨的方法中，超声波检测技术具有无损、便捷、对人体无害及设备成本低等优点，成为钢轨检测的首选方法［4］。为确保对钢轨进行全面探伤，对不同位置不同类型的钢轨缺陷选取不同类型的探头检测［5］。然而，目前了解超声探头的有效检测区域均普遍采用粗略的估计或者采用几何光学的声线计算来得知，而并没有对探头实际辐射至钢轨内声场分布的特性进行分析，极大地影响了钢轨超声检测的准确性［6］。因此，在钢轨缺陷的超声检测过程中，有必要开展钢轨内声场模拟的研究。研究探头声场特性的方法中，多元高斯声束模型是准确模拟声场的理论模型，同时能够描述声场声压在不同介质中的分布［7］。本文采用多元高斯声束理论建立不同类型探头辐射的声场的模型，并模拟其在钢轨内的分布，以此分析探头的有效检测区域，进而指导选择钢轨最优检测工艺，实现对轨头、轨腰及轨底内存在的缺陷进行检测和分析。

1 多元高斯声场理论模型建立

1.1 圆形平面探头声场建模

多元高斯声束模型可以快速模拟出探头辐射的声场，而且可以方便处理声束在多层介质传播问题;同时，其不仅可用于圆形活塞式探头声场的计算，而且可以准确地计算出矩形探头的声场［8－10］。采用基于传递矩阵的多元高斯声束模型可以方便地计算在多层介质中辐射的声场，用于计算圆形平面探头在第m+1层介质中质点处声压场，可以表示为

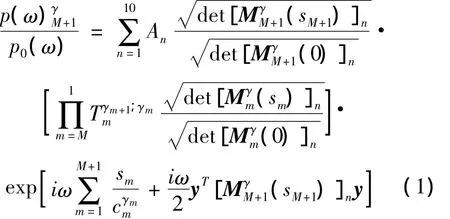
式中:Tγm+1;γmm表示声波(γ =p，s)在第 m 层界面处折射时的透射系数;sm表示在第m层介质中的声程;cγmm表示在第m层介质中声速;Mγmm(0)表示在m层界面处透射项;Mγmm(sm)表示在第m层介质中的传播项。M矩阵项均为2×2矩阵，且传播项和透射项均满足传递法则，采用全局矩阵描述在最后一介质中SM+1距离处的M矩阵为

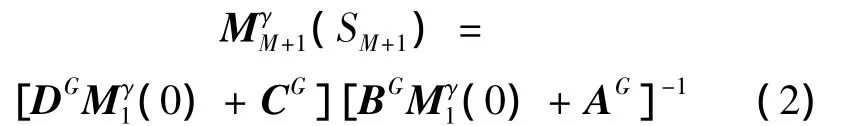
式中:AG，BG，CG和DG综合了所有的传播矩阵和透射矩阵而形成的4×4全局矩阵项，其表达式为

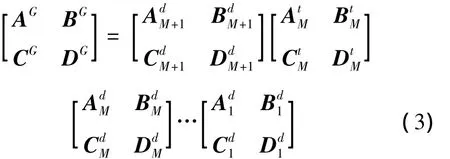
当两不同界面为平面时，传播矩阵和透射矩阵的表达式为

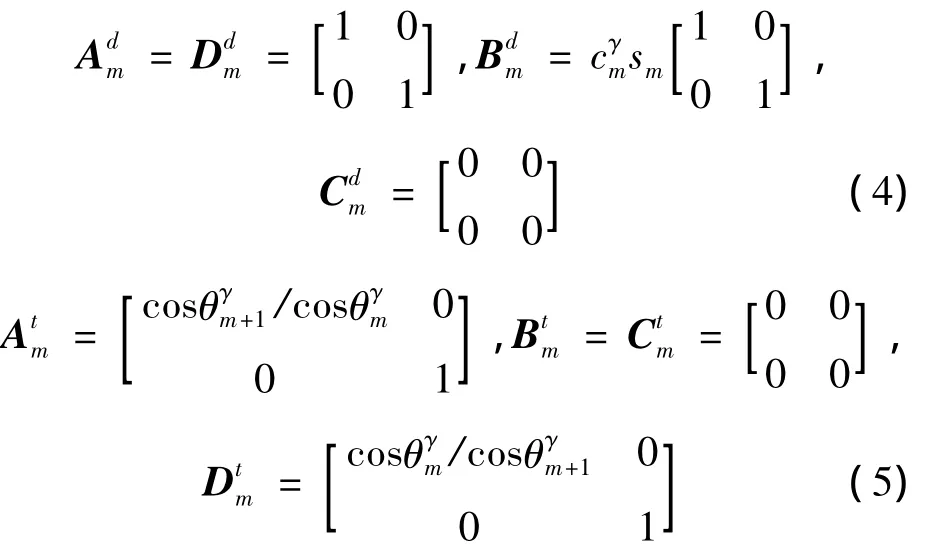
采用该式完成对所有M矩阵的计算。其中M矩阵的初始表达式为

式中:DR=ka2/2表示瑞利距离;An和Bn为10组高斯叠加复系数。

1.2 矩形平面探头声场建模

对于矩形平面探头，因矩形源表面的质点速度可以利用两个圆盘源的乘积来表示，进而可以将高斯叠加方法应用于矩形源，于是，在第m+1层介质中质点处声压场可以表示为［9］

M矩阵的初始表达式为

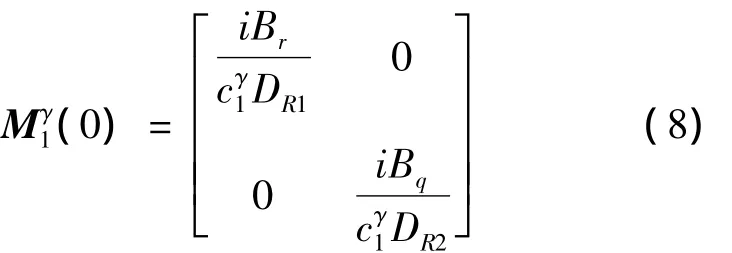
式中:DR1=ka21/2，DR2=ka22/2，表示瑞利距离;2a1和2a2分布矩形探头晶片的长和宽，其他参数与圆形平面探头一致。Ar，Br，Aq和Bq为同样采用10组高斯叠加复系数。

应用上述建立的多元高斯声束模型与钢轨几何外形参数相结合，当探头参数、钢轨等介质参数及入射角等已知的情况下，即能确定不同探头辐射的声场在钢轨内分布特性。

2 基于探头声场模拟的钢轨超声检测方案

2.1 钢轨内部缺陷分析

分析钢轨内部缺陷是有效实现检测的基础。图1所示为钢轨内部容易产生的缺陷及所在区域，其中包括轨底由于生产过程中钢坯轧制时折叠等因素导致的裂纹;轨头中部及轨腰区由于非金属夹杂物扎制脱落形成的内部裂纹;因承受着车辆轮对的冲击在轨头表面产生的疲劳裂纹以及轨头内两侧形成的体积性核伤等缺陷［2］。采用超声检测过程中，考虑钢轨工字型的外形结构，针对不同位置不同类型的钢轨缺陷，通常选用不同类型的探头。如核伤通常出现于轨头内侧的踏面下8～12 mm处，其方向通常与踏面成很小角度，因此，通常采用70°横波斜探头一次回波检测方法;对于轨头内部及轨腰内的裂纹，通常采用接触直探头检测;而对于轨底的裂纹，则以选用斜探头进行检测为主［5］。选取不同类型的探头，以确保对钢轨的全面检测，而在建立的多元高斯声束模型的基础之上，可以完成对探头辐射至钢轨内形成的声场可视化的研究，并根据模拟结果分析探头的有效检测区域，并进而设计钢轨的检测方案。

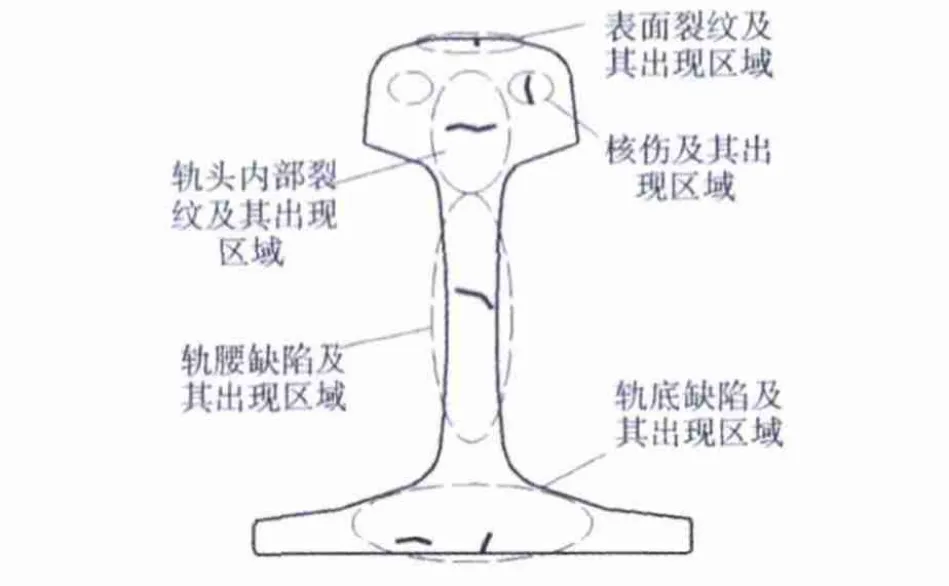
图1 钢轨内部主要缺陷及区域Fig.1 The main defects and distribution area in rails

2.2 矩形探头辐射至轨头内声场的模拟

采用接触式矩形斜探头对轨头内部偏两侧容易产生的体积性核伤进行检测，选用的探头频率为2.5 MHz，晶片长为12 mm，宽度为8 mm，声束沿晶片中心轴线在有机玻璃砌块经过10 mm声程后以约50°的入射角传入钢轨。其中钢的密度以7.85 g/cm3，纵波声速以5 900 m/s计，玻璃砌块密度为1.2 g/cm3，纵波声速为2 680 m/s。入射角度大于第一临界角，在钢轨内只形成约70°角的折射横波。依据传递矩阵及探头和介质参数等，采用式(7)进行在探头玻璃砌块及钢轨内声场声压的计算，不同声压以不同灰度颜色的形式显示，沿声束的中心轴线的轨头截面和侧面声场分布如图2所示。由图2可以看出:由于近场区的存在，钢轨与探头接触处出现检测盲区，而探头前方由于声束沿一定角度传播，使得该探头对钢轨表面处的缺陷仍难以检测出，但对于存在于8～12 mm处以70°形式存在的核伤，该斜探头能够有效的检测。对比图1可知:探头的声场覆盖了轨头两侧核伤容易形成的区域，能够对该区域进行有效检测。

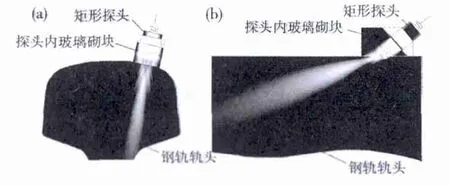
图2 矩形斜探头在轨头内辐射的声场特性Fig.2 The sound field characteristics in rail heads radiated by rectangular angle transducer

2.3 圆形探头辐射至轨头内部及轨腰区声场的模拟

选用接触式平探头对轨头内部及轨腰处可能存在的缺陷进行检测。为了解平面探头辐射入钢轨内产生的声场，选用晶片直径为10 mm、频率为2.5 MHz的接触式探头进行模拟。声束只在一层介质中传播，因此只考虑传播矩阵;结合探头和钢轨等各参数，采用式(1)进行探头辐射入钢轨后横截面上声压的计算，并以图3所示的灰度图像形式显示。由图3可以看出:探头声场覆盖了轨头内部中间部位并延伸至轨腰，因此，其有效检测出该部分区域的存在的缺陷。同时，如果选取晶片直径更大的探头进行检测，其覆盖的有效检测区域将有所增大。对比图1可知:该探头能够对轨头内部和轨腰容易出现缺陷的区域进行有效检测。

图3 圆形平探头在钢轨内辐射的声场特性Fig.3 The sound field characteristics in rails radiated by circular plane transducer

2.4 矩形探头辐射至轨底内声场的模拟

选用接触式矩形横波斜探头对轨底中部极易出现的裂纹进行检测，探头型号与检测轨头核伤探头一致。在探头参数及入射角度确定的情况下，采用式(7)进行探头玻璃砌块及钢轨内声场声压的计算，并以图像的形式显示，如图4所示。由图4可以看出探头辐射的声场覆盖了轨底内缺陷较容易出现的中心区域。对比图4和图1可知:该探头能够对轨底内容易出现缺陷的区域进行有效检测。

图4 矩形斜探头在轨底内辐射的声场特性Fig.4 The sound field characteristics in rail bases radiated by rectangular angle transducer

3 钢轨内部缺陷超声检测实验

3.1 钢轨试块及超声检测装置

选用60 kg/m的标准钢轨作为试块，长度为30 cm，试块内部设置的主要缺陷及位置如图5所示，其中包括:模拟轨头内核伤的1号缺陷(直径2 mm，深15 mm的70°钻孔)，模拟轨头表面缺陷的2号缺陷(直径2 mm，深5 mm的70°钻孔)，模拟轨头内部缺陷的3号缺陷(直径4 mm深15 mm钻孔)，模拟轨腰内部缺陷的4号缺陷(直径3 mm的横通孔)和模拟轨底缺陷的5号缺陷(直径3 mm，深10 mm钻孔)。超声探头选用上海汕超仪器设备有限公司生产的接触式圆形晶片平探头(2.5Z10N)及矩形晶片斜探头(2.5Z8 ×12)，其声场特性如上所述;采用上海思雀柯公司生产的UT2001可编程超声板卡，选取甘油作为耦合剂。实验过程中，探头由不同位置经耦合剂与钢轨接触，通过超声卡采集并存储接收的电压信号，并以A波形式显示。

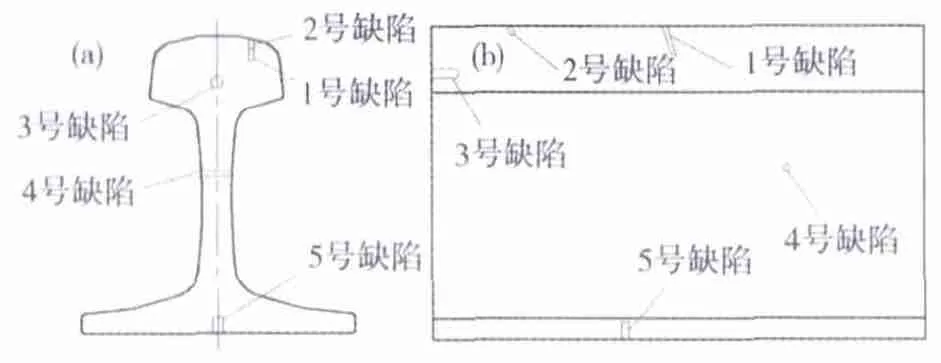
图5 钢轨试块及其缺陷分布Fig.5 Rail test block and its defects distribution

3.2 矩形探头对轨头核伤检测结果

由图2所示的声场模拟可以看出:轨头内10 mm以下的核伤在斜探头的有效检测区域内，能够实现对该缺陷的检测，采用接触式矩形斜探头对1号和2号缺陷进行超声检测加以验证。选择增益为20 dB，检测过程中探头所在位置如图2所示，通过沿钢轨径向方向移动探头，对两缺陷进行检测并以A波包络波形式显示，其结果如图6和图7所示。由图6和图7可以看出:由于近场的存在以及探头砌块与钢轨接触面的影响，在始波之后有明显的杂波干扰;而探头声束与钢轨表面呈一定角度，因此，对钢轨表面及近表面的缺陷并不能有效的检测。从图6可见:由于缺陷波较为明显，因而内部核伤缺陷信号能够被有效提取。从图7可见:由于无明显的缺陷波，故超声探头无法准确探测出钢轨近表面缺陷。

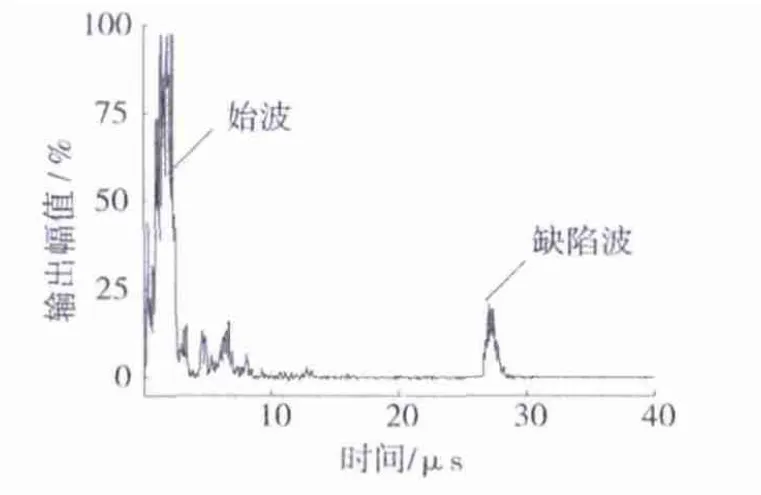
图6 1号缺陷A波Fig.6 A － wave of No.1 defect

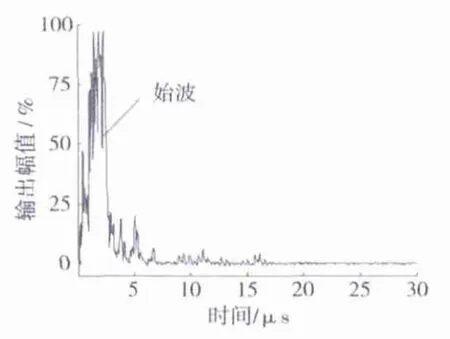
图7 2号缺陷A波Fig.7 A － wave of No.2 defect

探头接收来自规则界面反射的信号通常在频域上具有良好的特性，而缺陷的反射信号受其位置、大小和取向等影响在频域上表现出很强不固定性。为了更精确地判断缺陷波，对1号缺陷回波射频信号进行快速傅里叶变换。图8所示为矩形探头采集的始波信号的频域特征，图9所示为缺陷波的频域特性。由图8可以看出:虽然含有一定频率的噪声干扰，但其主要频率集中在2.5 MHz。而对于图9所示的缺陷波的频域特征，其并没有一个稳定的频域范围，由此可判断该波为缺陷回波。

3.3 圆形探头对轨头内及轨腰区检测结果

通过图3所示声场模拟结果可以看出，探头辐射至钢轨内的声场有效覆盖了轨头内部并延伸至轨腰。采用接触式圆形平探头对钢轨轨头及轨腰内的缺陷进行检测，探头位于轨头中心线处，调节增益为10 dB，对轨头内部缺陷进行检测。图10所示为对3号缺陷的A波包络形式检测结果，结果显示:缺陷反射回波明显，故探头对轨头内部缺陷能够进行有效检测。调节增益为20 dB，对轨腰内缺陷进行检测。图11所示为4号缺陷的A波包络形式的检测结果。从图10和图11可见:轨腰的缺陷反射回波被接收;同时，由于外形造成的声衰减，轨底反射回波幅值有所降低，而且轨头下部的反射回波被接收并形成干扰，此时，轨腰的缺陷如果与轨面垂直或缺陷较小，其回波幅值很小可能会被漏检。

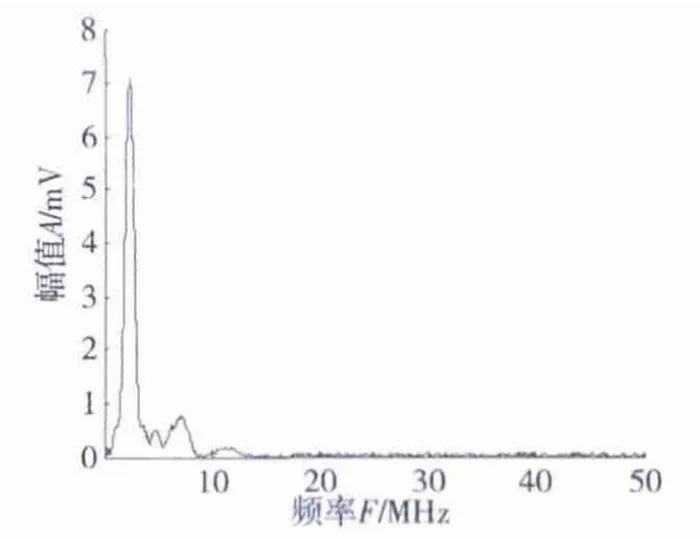
图8 1号缺陷结果始波频域特性Fig.8 Initial wave frequency characteristics of No.1 defect

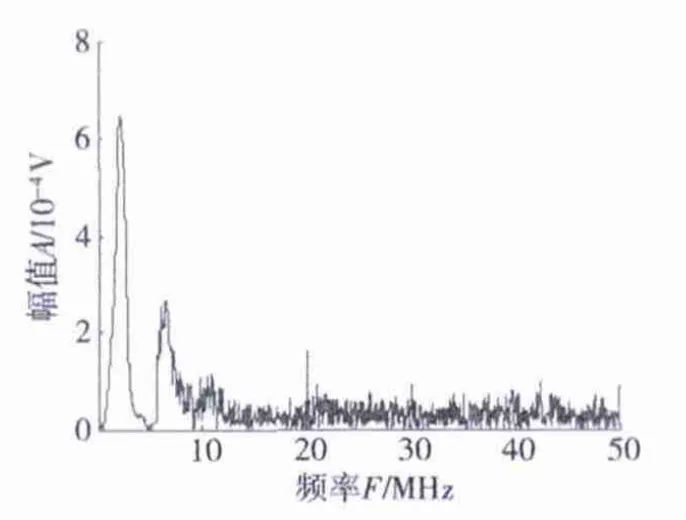
图9 1号缺陷结果缺陷波频域特性Fig.9 Flaw wave frequency characteristics of No.1 defect

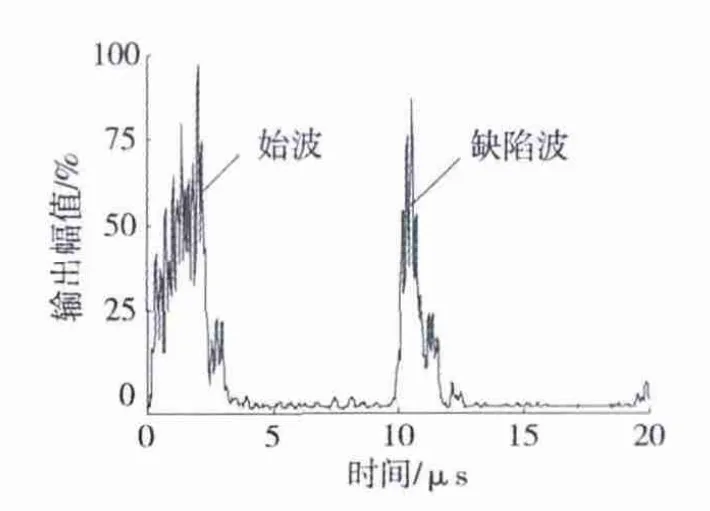
图10 3号缺陷A波Fig.10 A － wave of No.3 defect

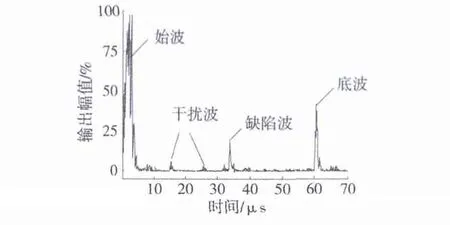
图11 4号缺陷A波Fig.11 A － wave of No.4 defect

同样地为判断3号缺陷检测结果的准确性，对其进行频谱分析研究。图12所示为平面直探头采集的始波信号的频域特征，图13所示为缺陷波的频域特性。由图12可以看出:始波在频域上呈现很好的特性;而缺陷波在频率上也集中在2.5 MHz。这主要是因为横通孔缺陷依然具有较好的反射特性，但其杂波在频域上影响还是较明显，仍然能够分辨出始波和缺陷波。而4号缺陷检测结果虽然能够区分始波和缺陷波，但是因干扰波的存在，在频域上也很难区分出干扰波和缺陷波。

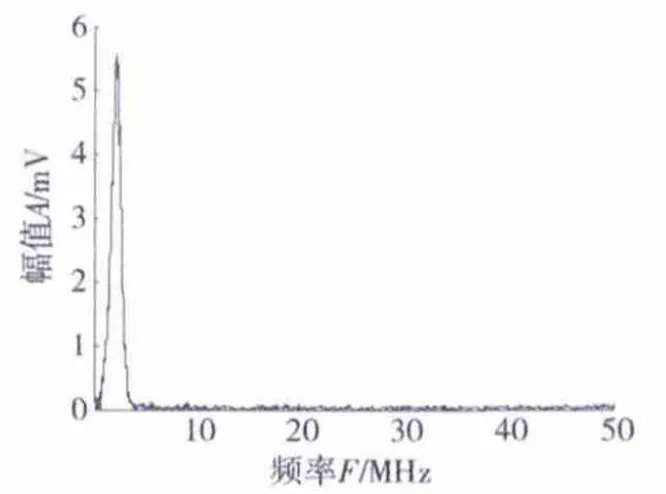
图12 3号缺陷结果始波频域特性Fig.12 Initial wave frequency characteristics of No.3 defect

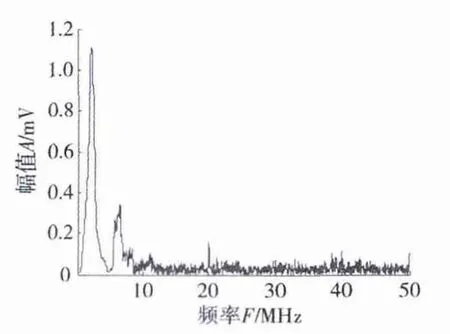
图13 3号缺陷结果缺陷频域特性Fig.13 Flaw wave frequency characteristics of No.3 defect

3.4 矩形探头对轨底缺陷检测结果

通过图4所示的声场模拟可知:斜探头能够有效地检测出轨底的大部分区域的缺陷。采用接触式矩形平探头对钢轨轨底缺陷进行检测(探头位置如图4所示)，利用15 dB增益对轨底的缺陷进行检测。图14所示为5号缺陷的A波包络形式检测结果，结果显示:由于探头与钢轨接触面粗糙度的影响，始波后的杂波干扰严重，同时造成声能的衰减较大;对于轨底内部的缺陷，能够有效地提取其反射回波，即缺陷波，可知该探头能够对轨底区域进行有效检测。

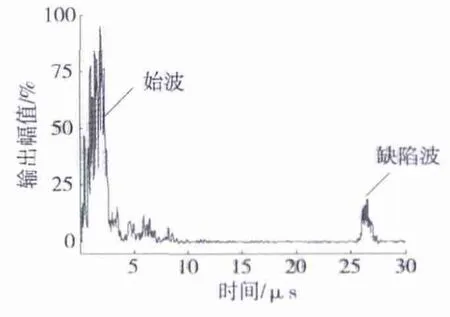
图14 5号缺陷A波Fig.14 A － wave of No.5 defect

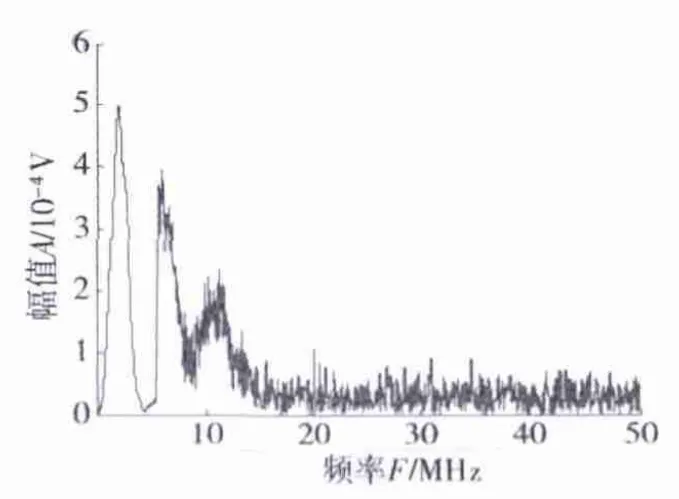
图15 5号缺陷结果缺陷频域特性Fig.15 Flaw wave frequency characteristics of No.5 defect

采用快速傅里叶变换对5号缺陷的射频回波进行分析，其频域特性如图15所示。该信号在频域上并没有表示特别集中的频率分布，与界面处回波频域特性(图8)有很大区别，因此，能够明显地对缺陷波进行识别。

4 结论

(1)通过引入多元高斯声场模型，开展了矩形和圆形接触探头辐射至钢轨轨头、轨腰及轨底声场特性的研究分析，从而有效地确定探头的检测区域。以此为依据，针对钢轨主要缺陷区域，对探头选择、探头位置布置及探伤增益调整等检测工艺进行设计分析。

(2)基于矩形和圆形接触探头的声场特性，开展了钢轨缺陷超声检测实验研究，A波检测结果及频谱分析显示:采用矩形和圆形接触探头及组合布置形式，能够对轨头内两侧的核伤、中部裂纹，轨腰区较大缺陷及轨底的裂纹等有效的进行检测，验证了该方法对钢轨内部缺陷超声检测的可行性。

(3)由于超声波检测方式对轨头近表面裂纹检测困难，同时因声束的扩散和衰减及轨头底部反射波影响，对于轨腰上的较小缺陷检测效果不明显。因此，对于不能确定的缺陷，应进行复检，以提高准确度。

［1］Clark R.Rail flaw detection:overview and needs for future developments［J］.NDT＆E International，2004，37:111－118.

［2］邓建辉.钢轨裂缝缺陷分析［J］.理化检验:物理分册，2002，38(8):360 －362.DENG Jianhui.Analysis on the crack in rail［J］.PTCA Physical Testing，2002，38(8):360 －362.

［3］Coccia S，Bartoli I，Marzani A，et，al.Numerical and experimental study of guided waves for detection of defects in the rail head［J］.NDT＆E International，2011(44):93－100.

［4］Fan Y，Dixon S，Edwards R S，et al.Ultrasonic surface wave propagation and interaction with surface defects on rail track head［J］.NDT＆E International，2007(40):471－477.

［5］黎连修，钱仁才，马清，等.钢轨核伤超声波检测研究［J］.铁道技术监制，1995(6):44 －46.LI Lianxiu，QIAN Rencai，MA Qing，et al.Study on corewound in rails using ultrasonic detection［J］.Railway Quality Control，1995(6):44 －46.

［6］王铁楠，刘杰.超声波探伤仪在高速钢轨检测中的应用［J］.现代机械，2007(4):11 －13.WANG Tienan，LIU Jie.An ultrasonic NDT system used in inspection of rails［J］.Modern Machinery，2007(4):11－13.

［7］Schmerr L W，SONG Sungjin.Ultrasonic nondestructive evaluation systems models measurement［M］.American:Springer，2007.

［8］Wen J J，Breazeale M A.A diffraction beam field expressed as the superposition of gaussian beam［J］.Journal of the Acoustical Society of America，1988(83):1752－1756.

［9］Ding D，Zhang Y，Liu J.Some extensions of the Gaussian beam expansion:radiation fields of rectangular and elliptical transducers［J］.J.Acoust.Soc.Am，2003(113):3043－3048.

［10］Huang R J，Schmerr L W，Sedov A.Multi－ Gaussian beam modeling for multi－ layered anisotropic media，I:Modeling foundations［J］.Research in Nondestructive E-valuation，2007，18(4):193 －220.