第三方物流选择的双层规划模型及其求解算法*

钟宇亮，刘诚

(中南大学数学与统计学院，湖南长沙 410083)

随着当当、凡客、京东、卓越等B2C电子商务企业的崛起，B2C(即企业与消费者之间的电子商务)已经成为了电子商务网购市场的一个亮点。据易观国际发布的报告数据显示，2010年中国B2C市场规模突破1 000亿元大关，达到1 040亿元，环比增长373%，而到2013年将达到6 500亿元［1］。少数大电商为节约物流成本，纷纷自建物流系统，而大部分B2C企业不具备自建物流体系的能力，但是，在销售的商品上具有成本优势，商品的成本价格加上物流价格依然比传统商务具有价格优势，这时，企业就可以采用第三方物流模式［2－3］，即将物流业务外包给专业的第三方物流提供商(the third part logistics service provides，TPLSP)，使得B2C企业可以专注于自己的核心业务，有效配置企业资源，提高企业的核心竞争力。然而，这一切价值的实现都是建立在合理的选择TPLSP的基础上，因此，B2C企业在采用TPLSP模式下，如何进一步选择合适的TPLSP将成为我们研究的重点。Vaidyanathan在IT环境下提出了TPLSP选择的概念框架［4］，彭玉兰等提供了一个综合评价 TPLSP的多指标体系，并建立了一个用模糊物元、粗糙集和TOPSIS法相结合的模型来选择和评价这些指标［5］，闫秀霞等提出了TPLSP选择的模糊多目标评价体系，建立了多目标决策模型，通过与理想多目标的对比建立了目标贴近度概念［6］，高丽娜等基于数据包络分析法(DEA)研究了TPLSP选择的方法［7］;胡健等优化了TPLSP选择指标体系，并构造了TPLSP选择的BP智能神经网络［8］;吴国通等利用层次分析法(AHP)选择适合的 TPLSP［9－10］。这些文献大多以定性研究为主，对如何定量地通过建立数学模型选择合适的TPLSP研究比较少。而事实上，大部分电商都是根据以往订单的接收情况和配送能力选择TPLSP，如许智超等研究了电子商务订单处理过程中的第三方物流中心的实时选择问题［11］，但是，选择的方法大多数是依赖以往的经验和相应的计算机软件系统来实时定性的选择TPLSP，更没有考虑第三方物流整体的利益。目前我国的第三方物流市场，提供B2C第三方物流服务的企业鱼龙混杂，因此，仅考虑电商的收益是不理性的，应该考虑B2C企业和TPLSP的全局利益，使得第三方物流市场良性发展，资源优化配置。本文在此基础上深入的定量的研究了这一问题，在遵循市场规律引入产品的需求－价格弹性因素下，建立了双层规划模型，使全局利益最优化，为电商企业选择合适的TPLSP提供了理论依据。

1 问题描述

某地区某段时间内，一个电商企业要从若干个备选的TPLSP中选择一个或多个分担其物流业务，从电商企业的角度出发，使得电商企业的利益最大化，同时从第三方物流市场整体的角度出发，使得整个TPLSP的利益也达到最大。显然，电商对TPLSP的选择问题涉及到2个具有明显不同目标函数的决策者:电商和第三方物流市场，因此采用双层规划模型描述这种关系是适宜的。把电商选择TPLSP问题看作一个Leader－Follower问题，其中电商决策部门是指导者(Leader)，物流量在各TPLSP的分配和客户需求在不同TPLSP的分配为跟随者(Follower)。电商决策部门可以通过选择不同的TPLSP来改变第三方物流市场的作业成本，根据客户的需求特点安排客户需求在TPLSP的分配。一般来讲，电商为取得自己的收益最大化会尽量地减少物流支付成本，即如何定价、如何选择TPLSP和物流量的分配。而第三方物流市场在电商的选择基础上，希望增加物流收入费用，同时降低物流作业成本来取得自己的最大利益。这对相互制约、相互影响的矛盾体如何找到平衡点就是本问题要解决的目标。

2 模型建立及求解

2.1 模型假设及符号说明

假设1:电商企业对某区域某段时间内客户需求商品种类以及TPLSP能够提供哪些种类的服务已经有了清楚的预测。

假设2:参选的TPLSP条件(配送质量，客户服务，企业信誉，增值服务能力等)没有差别，且客户网购货品时，邮费均由电商企业承担。

假设3:假设TPLSP的收入函数为一次函数Fi(xi)=wi+eixi［12］。其中:wi表示电商支付给TPLSP的固定费用，wi≥0，其不会随着产品数量的变动而变动，且系数ei＞0;xi≥0。

假设4:假定客户需求量为电商所给价格的减函数，其一般形式为Dj=Ij－kps。其中:Ij为第j个客户在价格为0时的需求量;k为常数;ps是电商单位产品的售价。记pc为电商单位产品的成本，则有pc＜ps＜。模型中的重要参数和符号如下:i为备选的 TPLSP 序号，i=1，2，…，I;j为客户(需求点)的序号，j=1，2，…，J;Qi为第 i个 TPLSP 的配送能力;ci为电商仓库到第三方物流中心i的单位运费;λi为第i个TPLSP单位物流的处理费用;hij为第i个TPLSP的物流中心到客户j的单位配送费用。

决策变量:zi为0－1变量，TPLSP被选中时，值为1，否则为0;xi为电商分配给第i个TPLSP的物流量;yij为第i个TPLSP配送到j客户的运量。

具体模型如下。

上层规划(U):

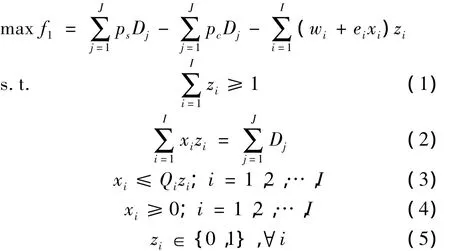
下层规划(L):

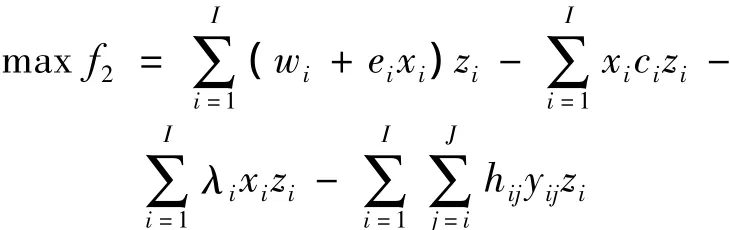
其中:M为任意大的正数。

上层规划(U)可以描述为电商决策部门选择合适的TPLSP获得的最大收益:第一部分为毛收入，第二部分为生产成本，第三部分为付给TPLSP的物流费用。式(1)保证至少选择1个TPLSP，式(2)表示所需物流量等于客户需求量，式(3)为配送能力的限制，式(4)为非负约束。

下层规划(L)则描述了在已选TPLSP的条件下物流量在TPLSP之间的分配以及客户需求在不同TPLSP之间的分配模式，使得第三方物流市场的收益最大:第一部分是整个第三方物流的总收入，第二部分运输费用，第三部分是物流处理费用，第四部分是配送费用。式(6)为容量限制公式，式(7)满足客户需求量，式(8)为物流量平衡式，式(9)保证分配量总是在备选TPLSP分配，式(10)为变量的非负约束。

2.2 模型求解

双层规划模型是一个复杂的优化模型。即使很简单的双层线性规划问题也是NP－hard问题，不存在多项式求解算法。由于双层规划问题的非凸性，所以即使能求出双层规划的解，通常也只可能是局部最优解，而非全局最优解。求双层规划问题的关键在于找到反应函数的具体形式，对于连续变量的情况，我们可以通过灵敏度分析法得出变量之间的导数关系，然后利用泰勒展式对反应函数进行近似，以求解双层规划问题，这是基于灵敏度分析方法的启发式算法SAB(sensitivity analysis based algorithm)，Yang等应用灵敏度分析方法求解了交通控制问题［13］;对于线性的双层规划，可以用罚函数求解。赵茂先等研究了用罚函数求解线性双层规划的全局优化问题［14］;高自友等也对不同双层规划模型设计过相应的罚函数法和启发式算法［15－17］。而本文模型中有些变量是离散的0－1变量，也非完全的线性双层规划，不能用上述的灵敏度分析方法和线性罚函数方法，所以应当设计符合该模型特点的启发式算法。

约束(9)表示平衡条件下，客户在各个物流企业分配的物流量与TPLSP选择方案之间的关系，由于yij=xi，则有xi≤Mzi。为了得到反应函数的具体形式，将它转化为下面的形式:

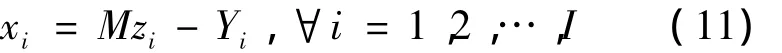
其中:Yi为松弛变量。当给定一组 Z0={z1，z2，…，zI}时，取集合S⊂Z0，S表示在给定初始值中被选的TPLSP的序号，约束(9)可以去掉，模型变为

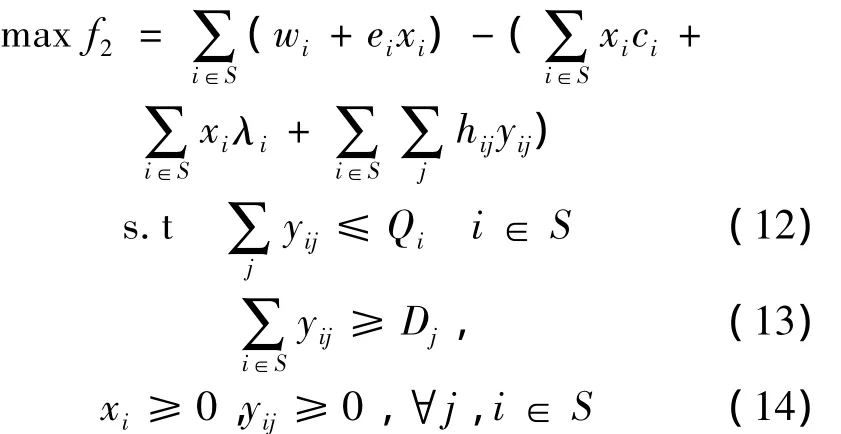
为了找到模型的最优解，根据模型的具体特点我们可以利用贪婪算法的思想设计启发式算法。

显然，在给定初始值 Z0={z1，z2，…，zI}条件下，wi是确定值，因此，记Hji=ei－(ci+λi+hij)，可以近似表示第i个TPLSP从电商企业仓库配送一个单位物流量到客户(需求点)j的收益，当zi=0时，Hji=0。贪婪算法思想:对每一个客户(需求点)j，我们选择TPLSP以Hji尽量大为标准，在此基础上，安排单位收益最大的TPLSP配送足够多的产品到相应的客户，同时电商分配相应多的产品给TPLSP。

根据贪婪算法可以求出相应的x'i，y'ij，根据式(11)，由x'i可以求出Y'i，这样就得到

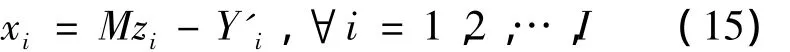
将式(15)代入上层目标函数中，利用Lingo软件求出新的一组 Zk={z1，z2，…，zI}，然后再一次求下层问题，就可以得到客户需求量在TPLSP的分配，即可得到被选TPLSP分担电商的物流量。如此反复上面的思路，最后有望收敛于双层规划模型的最优解。具体算法如下。

第1 步:给定一个初始解 Z0={z1，z2，…，zI}，令迭代次数k=0。

第2 步:初始化j=1，对给定的Z0，依次算出Hji，并重新排序(记下相应的序号)H1j≥H2j≥…≥HjI;i=1，xik=0;yijk=0。

第3 步:若 Dj≤ Qi，则 yijk=Dj，xik=xik+yijk，Dj=0，Qi=Qi－ xik，转第4 步;如果 Dj≥ Qi，则yijk=Qi，xik=xik+Qi，Dj=Dj－ Qi，Qi=0，i=i+1，转第3步。

第4 步:若 j≤J，j=j+1，转第2 步;若 j≥J，输出xik和yijk。

第5步:从下层问题求解出的xki，根据式(11)计算Yki，将关系式 xi=Mzi－ Yki代入上层目标函数，利用Lingo软件，得到一组新的Zk+1。

第6步:如果|f1k+1－f1k|≤ε，停止，转第1步;否则，令k=k+1，转第2步。其中ε为迭代精度。

由于本算法为启发式算法，初始解的选择对该算法收敛性和收敛速度有很大的影响，所以，在解决具体问题的时候需要选取不同初始解进行试算。

3 算例

假设系统中有 3个备选的 TPLSP(A1，A2，A3)，5 个需求点(B1，B2，B3，B4，B5)，备选 TPLSP的收入函数分别为 F1(x1)=15.2+3.1x1，F2(x2)=10.6+3.5x2，F3(x3)=12.4+3.2x3;客户(需求点)的基本需求分别为I1=220，I2=250，I3=280，I4=230，I5=200，k=10;电商仓库到 TPLSP物流中心的单位运费分别为 c1=0.5，c2=0.6，c3=0.7;备选TPLSP的物流配送能力为Q1=160，Q2=180，Q3=220;备选TPLSP单位物流量的处理费用分别为 λ1=0.3，λ2=0.4，λ3=0.5。备选TPLSP物流中心到各客户的单位配送费用hij如表1 所示，令 M=1 200，pc=13。

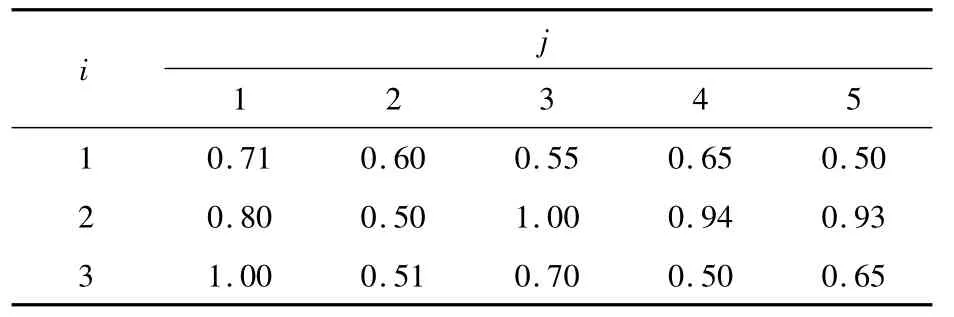
表1 单位配送费用Table 1 Unit delivery charges

其计算步骤如下。

步骤1:初始化。令 k=0，Z0=(1，1，1)，假定ps=14，计算出相应价格下的市场需求量D1=80，D2=110，D3=140，D4=90，D5=60。

步骤2:j=1，计算出Hji，并排序H12＞H11＞H13;D1＜ Q2，y21=80，x2=80，D1=0，Q2=100。

j=2，计算Hji，并排序H22＞ H21＞ H23;D2＞Q2，y22=100，x2=180，D2=10，Q2=0;D2＜ Q1，y12=10，x1=10，D2=0，Q1=150;

j=3，计算Hji，并排序H31＞ H32＞ H33，D3＜ Q1;y13=140，x1=150，D3=0，Q1=10;

j=4，计算Hji，并排序H43＞ H42＞ H41;D4＜Q3，y34=90，x3=90，D4=0，Q3=130;

j=5，计算Hji，并排序H51＞ H53＞ H52;D5＞Q1，y15=10，x1=160，D5=50，Q1=0;D5＜ Q3，y35=50，x3=140，D5=0，Q3=80。

得到均衡条件下需求点需求量在各TPLSP的分配以及各TPLSP承担的物流量为:

y12=10，y13=140，y15=10，y21=80，

y22=100，y14=90，y15=50，

x1=160，x2=180，x3=140。

求出反应函数表达式:

x1=1 200z1－1 040，x2=1 200z2－1 020

x3=1 200z3－1 060。

步骤3:将所得的反应函数线性关系代入上层规划的目标函数中，利用Lingo软件求得上层问题的一组新的选择z1=0，z2=1，z3=1。

步骤4:收敛判断，显然|f1k+1－ f1k|＞ 0.1，令k=k+1，转步骤 2。

步骤5:当|f1k+1－f1k|≤0.1时，重复以上4个步骤，求出不同ps下的选择方案如表2以及相应方案下f1和f2如图1所示。

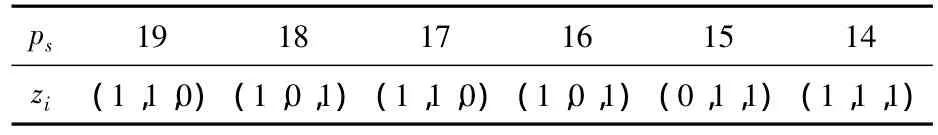
表2 不同价格下的选择方案Table 2 Options of different values

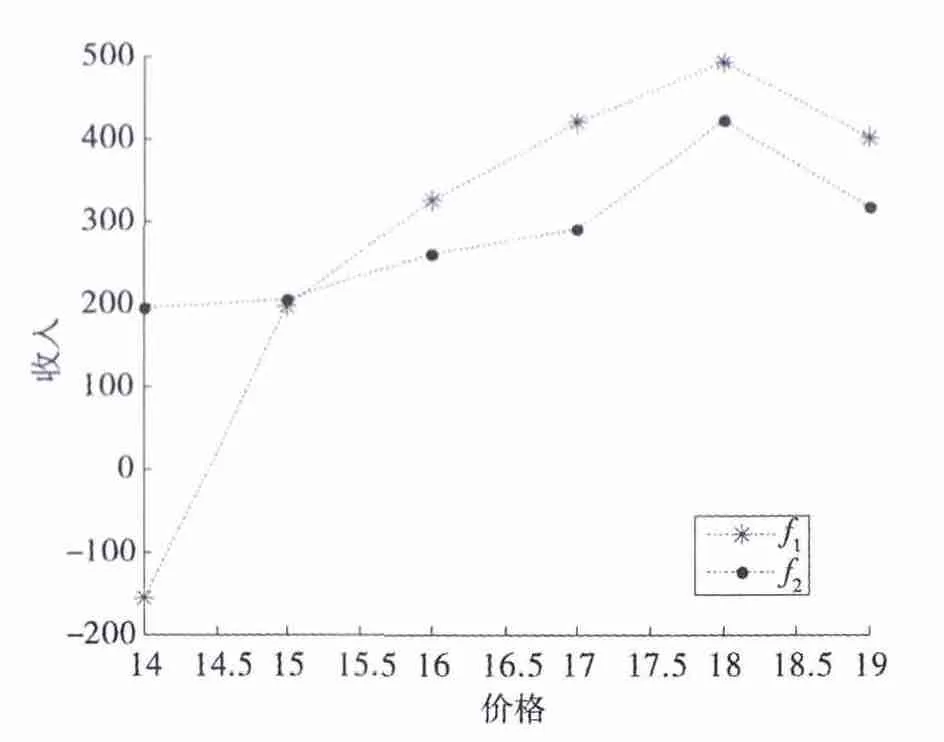
图1 相应价格下f1和f2Fig.1 The value of f1 and f2 under different values

最后，经过迭代，得到收益最大时的价格以及合理的TPLSP选择方案为:ps=18，z1=1，z2=0，z3=1，f1=494.2，此时被选的TPLSP所承担的物流量和需求点在各个TPLSP物流中心的分配为:

4 结论

(1)用双层规划模型定量地研究了B2C环境下TPLSP选择的问题，充分考虑了电商和TPLSP的全局利益，同时针对客户在产品价格弹性下对产品的不确定性需求，使模型在实际中更具有参考价值。

(2)所述模型仅在理想状况下考虑，还可讨论多个电商企业，多产品，TPLSP不同收入函数的情况，也可以考虑备选TPLSP配送质量、客户服务等条件有差别时的选择方案，以使其更符合实际情况。

［1］张宇，李琪.B2C电子商务企业物流配送模式选择研究［J］.人文杂志，2012，1(3):21 －26.ZHANGYu，LI Qi.Selection of B2Ce－commerce enterprise’s logistics mode［J］.Journal of Humanities，2012，1(3):21－26.

［2］吴秀程，项浩程.叶俗文.基于电子商务发展的四种物流模式［J］.中国物流与采购，2012，12(3):121 －123.WU Xiucheng，XAING Haocheng，YE Suwen.Four logistics models based on e － commerce development［J］.China Logistics＆ Purchasing，2012，12(3):121－123.

［3］Davis R.Setting up and managing outsourcing contracts to deliver value and accommodate change［J］.Journal of Corporate Real Estate，2004，6(4):301 －307.

［4］Vaidyanathan G.A framework for evaluating third－part logistics［J］.Communications of the ACM，2005，48(1):89－94.

［5］彭玉兰，陈治亚.第三方物流企业的选择和评价研究［J］.铁道科学与工程学报，2011，8(1):123 －128.PENG Yulan，CHEN Zhiya.Selection and appraisement of the third － party logistics［J］.Journal of Railway Science and Engineering，2011，8(1):123 －128.

［6］闫秀霞，孙林岩.第三方物流服务商选择的多目标决策研究［J］.中国机械工程，2004，15(12):1088 －1090.YAN Xiuxia，SUN Linyan.Multi－objective decisionmaking of third－party logistics service providers selected［J］.China Mechanical Engineering，2004，15(12):1088－1090.

［7］高丽娜，王亚超.基于DEA的第三方物流服务提供商选择方法研究［J］.价值工程，2006，4(2):92－97.GAO Lina，WANG Yachao.A method for selecting the third－ party logistics vendor based on DEA［J］.Value Engineering，2006，4(2):92 －97.

［8］吴国通，高雷阜.层次分析法在研究第三方物流服务提供商中的应用［J］.科学技术与工程，2005，13(2):23－26.WU Guotong，GAO Leifu.The application of analytic hierarchy process in choosing TPL supplier［J］.Science Technology and Engineering，2005，13(2):23 －26.

［9］胡健，史成东.第三方物流服务提供商的研究选择［J］.计算机工程与应用，2008，44(35):206 －208.HU Jian，SHI Chengdong.Selection of third－party logistics service provide［J］.Computer Engineering and Applications，2008，44(35):206 －208.

［10］Santy L M.An exposition of the AHP in reply to the paper remarks on the analytic hierarchy process［J］.Management Science，1990，36(3):259 －268.

［11］许智超，胡祥培，李广强，等.电子商务第三方物流中心实时选择研究［J］.哈尔滨工业大学学报，2005，37(11):232－238.XU Zhichao，HU Xiangpei，LI Guangqiang，et al.A method on real－time selection of third－party logistics center in e － commerce［J］.Journal of Harbin Institute of Technology，2005，37(11):232 －238.

［12］赵玉双，李军.浅析第三方物流合作中的支付函数［J］.科学技术与工程，2004，4(3):42 －46.ZHAO Yushuang，LI Jun.The analysis of pay function in TPL cooperation［J］.Science Technology and Engineering，2004，4(3):42 －46.

［13］Yang H，Yagar S.Traffic assignment and signal control in saturated road network［J］.Transportation Research，1995，29(A):125 －139.

［14］赵茂先，高自友.用罚函数求解线性双层规划的全局优化方法［J］.运筹与管理，2005，14(4):101 －104.ZHAO Maoxian，GAO Ziyou.A global convergent method for linear bi－level programs based on penalty function［J］.Operations Research and Management Science，2005，14(4):101 －104.

［15］孙会君，高自友.基于双层规划的供应链二级分销网络优化设计模型［J］.管理工程报，2004，18(1):68－71.SUN Huijun，GAOZiyou.An optimization model for two－echelon distribution network design in supply chain based on bi－ level programming［J］.Journal of Industrial Engineering/Engineering Management，2004，18(1):68－71.

［16］钟磊钢，李云岗，张翠华.基于价格弹性的双层规划二级分销网络模型［J］.计算机集成与制造系统，2006，12(10):103－108.ZHONG Leigang，LI Yungang，ZHANG Cuihua.Bilevel programming secondary distribution network model based on price elasticity［J］.Computer Integrated Manufacturing Systems，2006，12(10):103 －108.

［17］王广民，万仲平，王先甲.二(双)层规划综述［J］.数学进展，2007，36(5):513 －523.WANG Guangmin，WAN Zhongping，WANG Xianjia.Bibliography on bi－ level programming［J］.Advances in Mathematics(China)，2007，36(5):513 －523.