地铁车辆空气弹簧气压负载特性的分析与实验*

王晓东，吴冬华，唐进元，陈海锋

(1.南车青岛四方机车车辆股份有限公司技术中心，山东青岛 266111;2.中南大学高性能复杂制造国家重点实验室，湖南长沙 410083)

地铁车辆在额定工况和超载工况的粘着情况对车辆的牵引力和制动力尤为重要，为了充分利用车辆的粘着质量，最大限度地发挥车辆的牵引力，在车辆运营过程中需要对车辆的载质量进行检测［1］。目前，国内地铁车辆载质量的检测方法是根据检查空气悬挂系统上空气弹簧内气体压力，通过空气弹簧气压－负载特性曲线换算得到车辆的实际载质量，但是在实际加载过程中，发现检测的车辆重量与实际的车辆载荷情况存在较大的误差。本文通过对地铁车辆称重过程进行分析，结合实验数据，得到产生测量误差的主要原因，并推导出新的空气弹簧在称质量过程中的气压－负载公式，为准确测量地铁车辆的质量，最大限度地发挥车辆的牵引力和制动力提供参考。

1 地铁车辆空气弹簧称质量系统

地铁车辆称质量系统主要利用数据测量设备对安装在每列车体前后2个转向架上的空气弹簧压力进行检测。空气弹簧工作时，内腔充入压缩空气，形成一个压缩空气气柱。随着载荷量的增加，弹簧的高度降低，内腔容积减小，弹簧的刚度增加，内腔空气柱的有效承载面积加大，此时，空气弹簧的压力增大，承载能力增加。当载荷量减小时，弹簧的高度升高，内腔容积增大，弹簧的刚度减小，内腔空气柱的有效承载面积减小，此时空气弹簧的压力减小，承载能力减小。根据单个空气弹簧的静态性能试验，可以得到空气弹簧气压－负载特性曲线如图1所示，根据测试所得的空气弹簧压力，通过数据处理设备和运算分析软件，即可按照气压－负载特性曲线计算得到对应的载荷［2］。

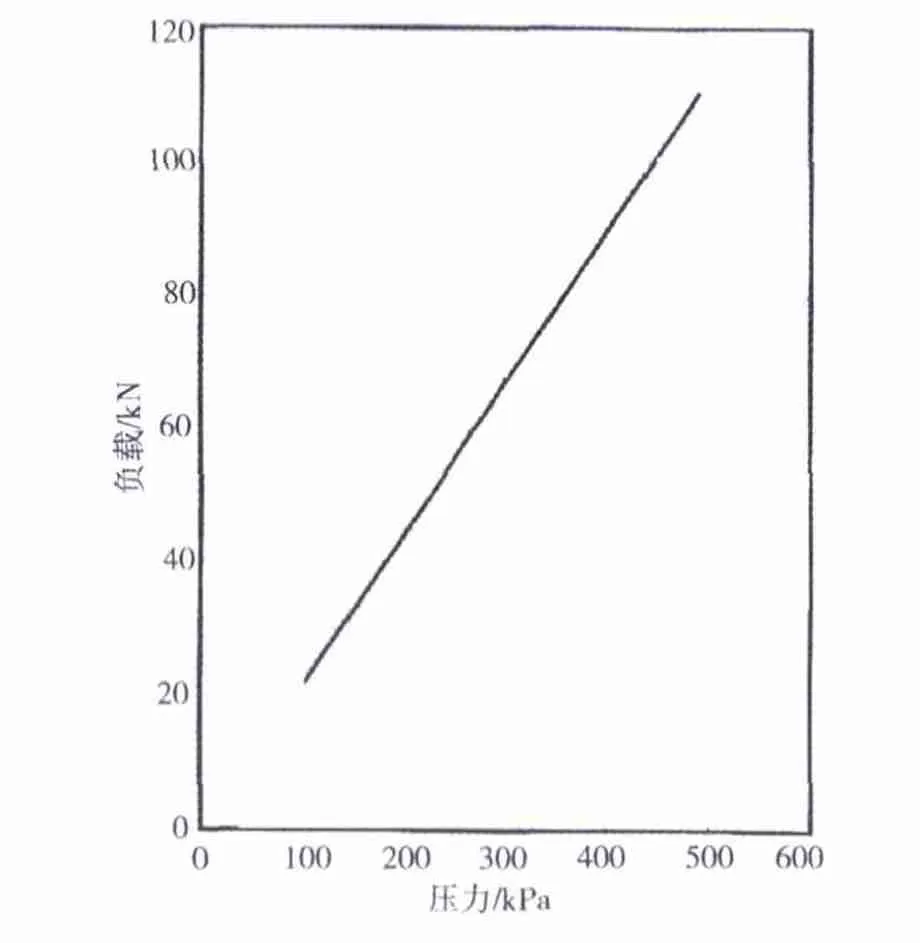
图1 空气弹簧静态气压－负载特性曲线Fig.1 Internal pressure－Load curve of static air spring

但是为了保证车体承载面高度不随载荷变化的特点，空气弹簧在使用过程中，随着载荷的增加或减少，高度阀控制的风缸不断的向空气弹簧充气、排气，使得空气弹簧高度保持不变［3－4］。风缸不断向空气弹簧充气、排气的过程造成空气弹簧内部质量发生变化，承载时的初始压强发生改变，由此引起气压－负载特性曲线发生变化。

2 空气弹簧动态气压－负载关系推导

在对空气弹簧气压－负载关系进行推导之前，进行如下定义与假设。

(1)定义静态气压－负载特性曲线为:在加、减载过程中，空气弹簧不存在充气、排气的过程，空气弹簧内部质量保持不变。

(2)定义动态气压－负载特性曲线为:在加、减载过程中，空气弹簧分别存在充气、排气过程，空气弹簧内部质量发生改变。

(3)在标准高度时，空气弹簧在实际支承载荷时其内压有效作用面积称为空气弹簧的有效面积，空气弹簧气室压力与有效面积的乘积即为空气弹簧轴向载荷。在此定义下，将空气弹簧等效为一个薄壁压力容器，呈圆柱状，壁厚即为空气弹簧橡胶帘线厚度，高度采用空气弹簧标准高度。

依据薄壁压力容器的薄膜应力和变形公式及理论，分别推导空气弹簧的静态气压－负载特性曲线与动态气压－负载特性曲线。

空气弹簧是一个形状不规则的变形体，在受载过程中，轴向与径向均有变形，为了简单表明空气弹簧压强与载荷的关系曲线，在此假设空气弹簧等效的圆柱体半径为r，高为h，模型示意图如图2所示。

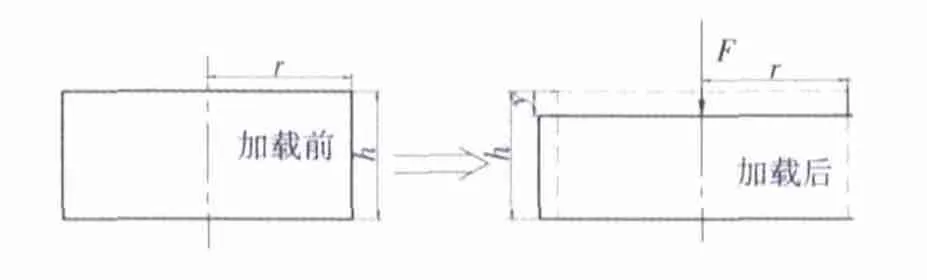
图2 空气弹簧等效模型Fig.2 Equivalent model of air spring

设在载荷F的作用下，空气弹簧稳定后，在半径方向的变形为x1，在轴向方向的变形为y，则变形后的横截面积可表示为

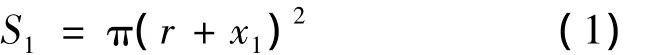
稳定后压强与载荷存在如下关系:

［5］知，薄壁压力容器在半径方向和轴向方向的变形是由轴向载荷和容器内压力的共同作用形成的。在本文中，因承重的载体为空气弹簧内的气体，因此，在考虑轴向载荷引起的变形时，主要为轴向载荷对空气弹簧内气体的变形，忽略了轴向载荷对橡胶囊的变形，考虑容器内压力的作用时，主要为压力对橡胶囊的变形，因此，得到变形与载荷、压力的关系如下:

式中:S承为空气弹簧上板与载荷的接触面积，把式(1)和(2)代入式(4)后可得到未充气时空气弹簧内气体压强p1与承载载荷F1的关系，即空气弹簧的静态压力－负载关系式为

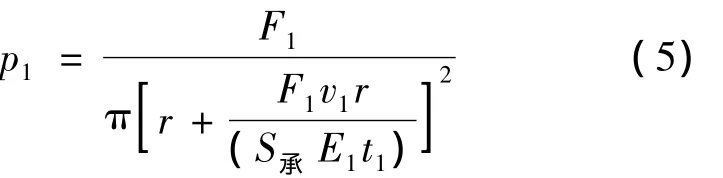
式中:E1，t1和υ1分别表示空气弹簧内气体的弹性模量、厚度和泊松比;E1与压强p的关系为E1=γ·p(1＜ γ ＜)［6］;E2，t2和 υ2分别表示空气弹簧橡胶囊的弹性模量、厚度和泊松比。

在动态过程中，气缸向空气弹簧充气，空气弹簧内压强为p2，在压强的作用下回到原来高度，设空气弹簧在半径方向的变形为x2，垂直方向的变形为y2，有如下关系式:

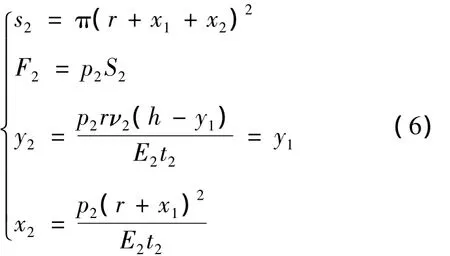
整理后可得到压强与载荷的关系为

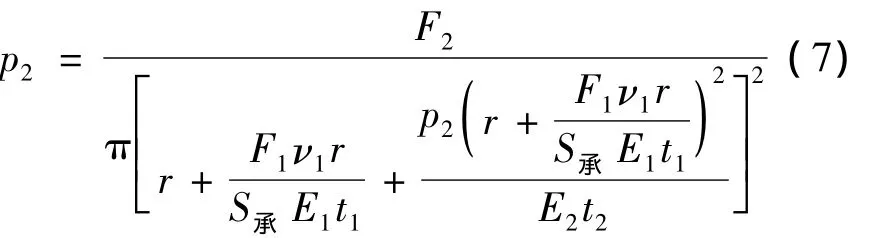
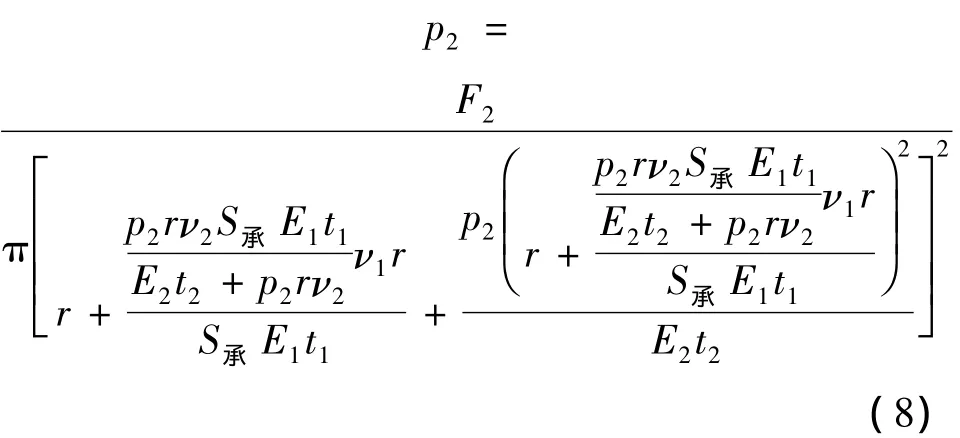
由参考文献［7］可以得到橡胶空气弹簧帘线橡胶板的材料性能参数。式中:E1=0.6 MPa，E2=280 MPa，t1=0.26 m，t2=0.006 m，υ1=0.01，υ2=0.5，Sc=0.38465 m2，r=0.27 m，h=1.095 m。将相关参数分别代入式(5)和(8)，运用Matlab软件进行计算，可以得到如图3所示空气弹簧的静态、动态气压和负载之间的关系曲线。

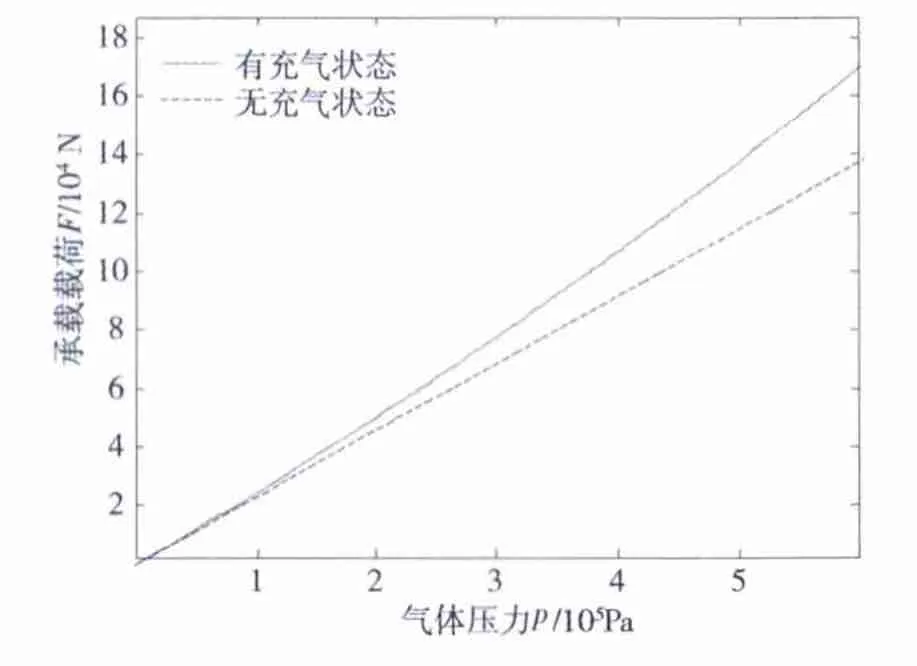
图3 空气弹簧气压－负载曲线Fig.3 Internal pressure－Load curve of air spring

由图3可以看出:静态气压－负载曲线基本呈线性关系，而动态气压－负载曲线由于考虑了充气后空气质量的变化，呈非线性的关系。在称质量过程中，空气弹簧的高度、内腔容积、承载能力随着振动载荷的递增与减小发生了平稳的柔性传递。通过阀口与风缸之间的充气排气，保证了空气弹簧的高度几乎不变，在充气或者排气后，空气弹簧弹簧的刚度和承载力都得到调整。因此，在载荷计算时，采用动态气压－负载曲线将更加准确。

为了验证动态气压－负载曲线的正确性，对北京地铁大兴线4号线065车的M3，M1和Tc1这3节车体的空气弹簧压力进行检测，分别代入式(5)和式(8)进行计算，得到采用不同计算方法得到的计算结果与实际质量的对比曲线如图4所示。

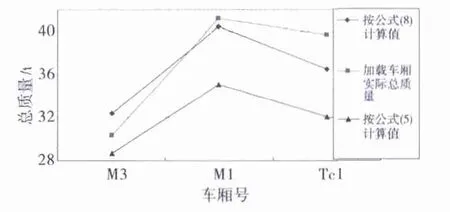
图4 空气弹簧负载计算对比Fig.4 Load contrast of air spring

由图4可知:采用动态气压－负载曲线后，由于考虑了空气弹簧在工作过程中的质量变化，计算得到的车体质量更加接近于实际情况。

3 结论

本文将空气弹簧简化为圆柱体，分别推导了空气弹簧的静态和动态气压－负载特性计算公式，其中动态气压－负载特性计算公式考虑了空气弹簧在工作过程中的充、排气过程，以北京地铁大兴线4号线065车体为例，分别采用静态和动态气压－负载特性曲线对车体质量进行了计算，通过与真实车体重量对比，表明本文推导的动态气压－负载特性曲线更加接近于实际情况，可以大幅度减小地铁车辆称重误差。

参考文献:

［1］陶功安.称重调簧装置在地铁车辆转向架上的应用［J］.电力机车与城轨车辆，2003，26(3):47，53.TAO Gongan.The application of test bench to metro vehicle’s bogie［J］.Electric Locomotives ＆ Mass Transit，2003，26(3):47，53.

［2］陈嫦.地铁车辆空气弹簧承重系统动力学分析及称重误差研究［D］.长沙:中南大学，2011.CHEN Chang.Study of weighing error and dynamic analysis of air spring load － bearing system of subway［D］.Changsha:Central South University，2011.

［3］刘增华，李芾，黄运华.空气弹簧及其在轨道车辆上的应用［J］.电力机车与城轨车辆，2003，26(6):24－27.LIU Zenghua，LIFu，HUANGYunhua.Application of air springs on rail bound vehicles［J］.Electric Locomotives＆ Mass Transit，2003，26(6):24 －27.

［4］陈嫦，唐进元，王祁波，等.铁道车辆空气弹簧动力学键合图建模及仿真［J］.铁道科学与工程学报，2011，8(2):98－103.CHEN Chang，TANGJinyuan，WANGQibo，et al.Bond graph dynamic modeling and simulation analysis of railway vehicle air spring［J］.Journal of Railway Science and Engineering，2011，8(2):98 －103.

［5］W.杨，R.布迪纳斯.罗氏应力应变公式手册［M］.北京:科学出版社，2005.Young Warren C.Roark’s formulas for strain and stress［M］.Beijing:Science Press，2005.

［6］王建岭，杨秀芹.气体弹簧的弹性模量［J］.平顶山工学院学报，2005，14(2):65 －66.WANG Jianlin，YANG Xiuqin.Elastic modulus of air spring coil［J］.Journal of Pingdingshan Institute of Techonology，2005，14(2):65 －66.

［7］Kulikovgm.Computational models for multilayered composite shells with application to tires［J］.Tire Science Technology，1996，24(1):11 －38.