有关偶完全数尾数的结论

张四保

(喀什师范学院数学系，新疆 喀什 844007)

设N+是全体正整数的集合.若，如果n满足关系式则n被称为完全数［1］.此时，若n是偶数，则n称之为偶完全数，根据经典的Euclid与Euler定理可知，每个偶完全数的形式均为n=2p-1(2p-1)，其中2p-1为Mersenne素数，并以Mp记之;若n是奇数，则n被称之为奇完全数.至今只发现47个偶完全数［2］，但尚未发现奇完全数，和未给出奇完全数是否存在的合理性证明.是否存在奇完全数，这已成为数论中的难题之一［3］.

对于偶完全数尾数的讨论，文献［4-5］分别讨论了偶完全数的个位与十位数字的情况，并给出了相应的结论;并且文献［5］中指出，根据文中的方法，可以大致的推断出偶完全数百位、千位…等各个位次上数字的大概情况.但是文献［5］中并未给出偶完全数的素指数p的取值情况.本文通过对素指数p取值情况的讨论，并调用、执行中国剩余定理的C语言程序来确定偶完全数百位数字取值情况.

1 主要结论及其证明

定理 设n=2p-1(2p-1)是偶完全数.若n的素指数p满足

则n的百位数字为0;

若n的素指数p满足

则n的百位数字为1;

若n的素指数p满足

则n的百位数字为2;

若n的素指数p满足

则n的百位数字为3;

若n的素指数p满足

则n的百位数字为4;

若n的素指数p满足

则n的百位数字为5;

若n的素指数p满足

则n的百位数字为6;

若n的素指数p满足

则n的百位数字为7;

若n的素指数p满足

则n的百位数字为8;

若n的素指数p满足

则n的百位数字为9.

证明 由于当偶完全数n=2p-1(2p-1)的素指数p=2、3时，n分别为n=6 ＜100、n=28 ＜100，那么考虑p≥5的情况.将素指数p分为p=8k+1，p=8k+3，p=8k+5 与p=8k+7.当p≥5时，n=2p-1(2p-1)取模8有下列关系式

n=2p-1(2p-1)取模125可以分为2p-1与Mp=2p-1分别取模125.结合素指数p=8k+1，p=8k+3，p=8k+5与p=8k+7的4种情况，2p-1取模125有下列关系式:

从式(2)可知，只需考虑6k取模125的情况.对于6k取模125的情况，文献［6］给出了当 k≡0，1，2，3，4，5，6，7，8，9，10，11，12，13，14，15，16，17，18，19，20，21，22，23，24(mod25)时，6k取模 125 的情况分别为 6k≡1，6，36，91，46，26，31，61，116，71，51，56，86，16，96，76，81，111，41，121，101，106，11，66，21(mod125)［6］，因而式(2)等价于下面式(3)—式(6):

而对于Mp=2p-1取模125的情况有下面式(7)-(10)［6］:

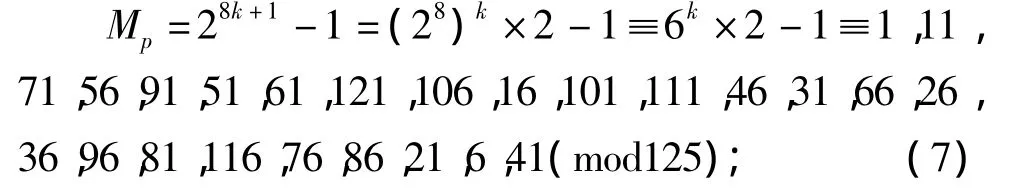
将式(3)与式(7)组合有，

将式(4)与式(8)组合有，

将式(5)与式(9)组合有，

将式(6)与式(10)组合有，

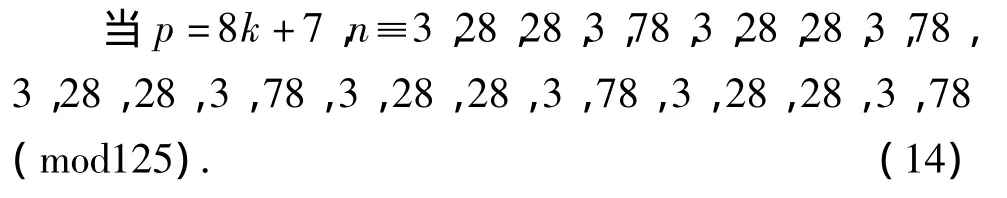
将式(1)分别与式(11)-(14)构成方程组.为了解出式(1)与式(11)所组成的第一个同余式组，通过调用、执行文献［7］所给出的有关中国剩余定理的C语言程序，输入运行得如下结果:

其中的Enter部分表示需要用户输入的信息，最后一行为所求的x的值.类似的，重复以上步骤，将所得的结果加之中国剩余定理的应用整理如下:

由于当 k≡0，5，10，15，20(mod25)时，p=8k+5一定是合数，故除去这5种情况.对上面式(15)-(18)分析，对百位数字分别是1至9的情况进行归类可以得到本文定理.

2 几个推论

推论1 若偶完全数n的百位数字是0，2，4，6，7，8，9，那么n的素指数p只能是4k+1型素数.

对文献［5］中的结论进行强化，给出了如下2个推论.

推论2 偶完全数n=2p-1(2p-1)的最后两位数是28的充分必要条件是n的素指数p是4k+3型素数.

推论3 每个大于6且以6结尾的偶完全数n=2p-1(2p-1)，

若素指数p满足

则其十位数字必为7;

若素指数p满足

p=8k+1，k≡3，8，13，18，23(mod25)或 p=5，则其十位数字必为9.

［1］ 单 墫.初等数论［M］.南京:南京大学出版社，2000.

［2］ 南丽丽.对完全数几个特性的C-语言验证［J］.运城学院学报，2010，28(5):80-81.

［3］ DICKSON L E.History of theory of number［M］.Washington:Washington Carnegie Institution，1919.

［4］ 杜君花.关于偶完全数尾数的探讨［J］.高师理科学刊，2004，24(3):13.

［5］ 张四保，罗 霞.偶完全数的两个注记［J］.河北北方学院学报:自然科学版，2008，24(6):4-5.

［6］ 张四保，邓 勇.Mersenne素数的一点注记［J］.华中师范大学学报:自然科学版，2011，45(3):371-373.

［7］ 颜松远.计算机在数论中的应用［J］.计算机应用研究，1993(2):1-9.