关于不定方程x2-pqy4=16的正整数解
2022-12-26管训贵潘小明
管训贵,潘小明
(泰州学院 数理学院,江苏 泰州 225300)
设p,q为奇素数,m为大于1的整数,满足q=p+2m。有一类典型的椭圆曲线是
y2=x(x+εp)(x+εq),ε∈{-1,1}
(1)
在确定式(1)的整数点时,曾分解出一种情形:
x=pqa2,x+εp=2spb2
x+εq=2sqc2,y=±2spqabc
此情形最终归结为讨论不定方程
的正整数解。当s=0,1时,此方程的讨论比较简单;而s=2时,则较为复杂。基于上述考虑,本文讨论不定方程
x2-pqy4=16,gcd(x,y)=1,x,y∈N*
(2)
的解。当然,式(2)也是不定方程的基本类型之一[1-3]。本文用初等方法对式(2)的解进行了探究,获得以下一般性的结果。
1 主要结论
定理设p,q为奇素数,m为大于1的整数,且q=p+2m。若不定方程
X2-pqY2=16,gcd(X,Y)=1,X,Y∈N*
u1≡3(mod 4),v1≡2(mod 4)
或
u1≢3(mod 8),v1≡4(mod 8)
或
u1≢7(mod 8),v1≡0(mod 8)
则式(2)的解必满足
y2=un+(p+2m-1)vn,n≥0
根据定理直接可得:
推论1不定方程
x2-33y4=16,x,y∈N*
(3)
仅有解(x,y)=(7,1)和(92,4)。
推论2不定方程
x2-209y4=16,x,y∈N*
(4)
仅有解(x,y)=(15,1)。
推论3不定方程
x2-65y4=16,x,y∈N*
(5)
仅有解(x,y)=(9,1)和(516,8)。
2 一些引理

X2-DY2=M,M∈N*
(6)



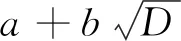
(ⅰ)un+2=2aun+1-un,u0=1,u1=a;vn+2=2avn+1-vn,v0=0,v1=b。
(ⅲ)u-n=un,v-n=-vn。
(ⅴ)un+2km≡(-1)kun(modum);vn+2km≡(-1)kvn(modum)。
引理4[5]设D>0且不是平方数,则不定方程
x2-Dy4=1
(7)

由引理4即得引理5。
引理5不定方程x2-33y4=1仅有正整数解(x,y)=(23,2)。
证明因为33≠1 785,28 560,且v2=23×23为非平方数,故由引理4知,该不定方程至多有一组正整数解。又由232-33×24=1知结论成立。证毕。
类似可证引理6。
引理6不定方程x2-65y4=1仅有正整数解(x,y)=(129,4)。
引理7[6]设p,q为不同的奇素数,若p≡3(mod 4),q≡3(mod 4),则不定方程x4-pqy2=1没有正整数解(x,y)。
引理8[7]设整数a>1,则不定方程
ax2-Dy4=1
(8)

引理9不定方程
x2-836y4=1
(9)
无正整数解(x,y)。

x+1=418r4,x-1=2s4
(10)
或
x+1=2s4,x-1=418r4
(11)
或
x+1=38r4,x-1=22s4
(12)
或
x+1=22s4,x-1=38r4
(13)
这里,s,r∈N*,gcd(s,r)=1,y=rs。
若式(10)成立,则得s4-209r4=-1。取模11,有s4≡-1(mod 11),不可能。
若式(11)成立,则得s4-209r4=1。由于11≡3(mod 4),19≡3(mod 4),故由引理7知,不可能。

若式(13)成立,则得
11s4-19r4=1
(14)
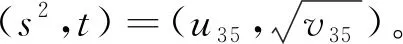

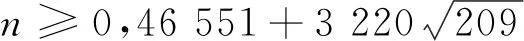
vn=35xn+506yn
(15)
并且有序列:
xn+2=93 102xn+1-xn,x0=1,x1=46 551
yn+2=93 102yn+1-yn,y0=0,y1=3 220
(16)
利用式(16)对式(15)取模8,得v35≡5(mod 8),即v35不是完全平方数。因此,式(14)无正整数解。证毕。
引理10不定方程
x2-209y4=1
(17)
无正整数解(x,y)。

x+1=1 672r4,x-1=2s4
(18)
或
x+1=2s4,x-1=1 672r4
(19)
或
x+1=418r4,x-1=8s4
(20)
或
x+1=8s4,x-1=418r4
(21)
或
x+1=152r4,x-1=22s4
(22)
或
x+1=22s4,x-1=152r4
(23)
或
x+1=88r4,x-1=38s4
(24)
或
x+1=38s4,x-1=88r4
(25)
这里,s,r∈N*,gcd(s,r)=1,y=2rs。
若式(18)成立,则得s4-836r4=-1。取模11,有s4≡-1(mod 11),不可能。
若式(19)成立,则得s4-836r4=1。根据引理9知,不可能。
若式(20)成立,则得4s4-209r4=-1。取模11,有4s4≡-1(mod 11),不可能。
若式(21)成立,则得4s4-209r4=1。取模4,有r4≡-1(mod 4),不可能。

若式(23)成立,则得11s4-76r4=1。取模4,有s4≡-1(mod 4),不可能。

若式(25)成立,则得19s4-44r4=1。取模4,有s4≡-1(mod 4),不可能。
因此,式(17)无正整数解。证毕。
3 定理的证明
因为(p+2m-1)2-p(p+2m)·12=16,且不定方程
X2-pqY2=16,gcd(X,Y)=1,X,Y∈N*
(26)
仅有2个非结合类的解,所以根据引理2,式(26)的一般解可表示为

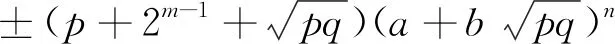
或


若式(2)有解,必有n,使得
y2=±(un+(p+2m-1)vn)
或
y2=±(un-(p+2m-1)vn)
=±(u-n+(p+2m-1)v-n)
当n≥0时,un+(p+2m-1)vn>0;当n<0时,un+(p+2m-1)vn<0。因此可归结为:
y2=un+(p+2m-1)vn,n≥0
(27)
或
y2=-un+(p+2m-1)vn,n>0
(28)
由引理3的(ⅰ)知:
un+2=2aun+1-un,u0=1,u1=a
(29)
vn+2=2avn+1-vn,v0=0,v1=b
(30)
当u1≡3(mod 4),v1≡2(mod 4)时,对式(29)取模4,得剩余序列的周期为2:1,3,…;对式(30)取模4,得剩余序列的周期为2:0,2,…。此时,式(28)成为y2≡3(mod 4),不可能。
当u1≡1(mod 8),v1≡4(mod 8)时,对式(29)取模8,得剩余序列的周期为1:1,1,…;对式(30)取模8,得剩余序列的周期为2:0,4,…。此时,式(28)成为y2≡7,3(mod 8),不可能。
当u1≡5(mod 8),v1≡4(mod 8)时,对式(29)取模8,得剩余序列的周期为2:1,5,…;对式(30)取模8,得剩余序列的周期为2:0,4,…。此时式(28)成为y2≡7(mod 8),不可能。
当u1≡7(mod 8),v1≡4(mod 8)时,对式(29)取模8,得剩余序列的周期为2:1,7,…;对式(30)取模8,得剩余序列的周期为2:0,4,…。此时,式(28)成为y2≡7,5(mod 8),不可能。
当u1≢7(mod 8),v1≡0(mod 8)时,式(28)成为y2≡3,5,7(mod 8),也不可能。
证毕。
4 推论的证明
先证推论1。若2|y,则有4|x。令x=4x1,y=2y1,则式(3)可化为
(31)
根据引理5,式(31)给出x1=23,y1=2。此时可得式(3)的解为(x,y)=(92,4)。

y2=un+7vn,n≥0
(32)
根据引理3,有
un+2=46un+1-un,u0=1,u1=23
(33)
vn+2=46vn+1-vn,v0=0,v1=4
(34)
v2n=2unvn
(35)
(36)
u-n=un,v-n=-vn
(37)
un+2km≡(-1)kun(modum)
vn+2km≡(-1)kvn(modum)
(38)
约定:下文中“T”表示取模所得剩余序列的周期。
利用式(33)和式(34),对式(32)取模151,得T=8,且当n≡1,4,6,7(mod 8)时,y2≡51,150,71,146(mod 151)均为模151的平方非剩余,故排除,剩n≡0,2,3,5(mod 8)。
对式(32)取模7,得T=8,且当n≡3,5(mod 8)时,y2≡5(mod 7)为模7的平方非剩余,故排除,剩n≡0,2(mod 8),即n≡0,2,8,10,16,18(mod 24)。
对式(32)取模433, 得T=24,且当n≡2,8,10(mod 24)时,y2≡180,344,231(mod 433)均为模433的平方非剩余,故排除,剩n≡0,16,18(mod 24)。
对式(32)取模1 153,得T=48,且当n≡16,40(mod 48)时,y2≡964,189(mod 1 153)均为模1 153的平方非剩余,故排除n≡16(mod 24),剩n≡0,18(mod 24),故n≡0(mod 6)。
若n≠0,可设n=2×3t(3k±1)(t≥1),并取m=3t,则m≡3(mod 6)。
利用式(37)和式(38),可将式(32)化为
y2≡±(u±2m+7v±2m)
≡±(u2m±7v2m)(modu3m)
(39)




矛盾。因此n=0。代入式(32),得y=1。此时可得式(3)的解(x,y)=(7,1)。
综上,方程(3) 仅有解(x,y)=(7,1)和(92,4)。证毕。
再证推论2。若2|y,则有4|x。令x=4x1,y=2y1,则式(4)可化为
(40)
根据引理10,式(40)无正整数解,故此时式(4)无解。

y2=un+15vn,n≥0
(41)
根据引理3,有
un+2=93 102un+1-un,u0=1,u1=46 551
(42)
vn+2=93 102vn+1-vn,v0=0,v1=3 220
(43)
v2n=2unvn
(44)
un+2km≡(-1)kun(modum)
vn+2km≡(-1)kvn(modum)
(45)
利用式(42)和式(43),对式(41)取模59,得T=4,且当n≡1,2(mod 4)时,y2≡38,58(mod 59)均为模59的平方非剩余,故排除,剩n≡0,3(mod 4),即n≡0,3,4,7,8,11,12,15,16,19(mod 20)。
对式(41)取模41,得T=40,且当n≡3,23,8,28,12,32,16,36,19,39(mod 40)时,y2≡14,27,12,29,6,35,30,11,27,14(mod 41)均为模41的平方非剩余,故排除,剩n≡0,4,7,11,15(mod 20)。
对式(41)取模281,得T=40,且当n≡7,27,11,31,15,35(mod 40)时,y2≡21,260,104,177,278,3(mod 281)均为模281的平方非剩余,故排除n≡7,11,15(mod 20),剩n≡0,4(mod 20)。
对式(41)取模601,得T=40,且当n≡4,24(mod 40)时,y2≡7,594(mod 601)均为模601的平方非剩余,故排除n≡4(mod 20),剩n≡0(mod 20)。
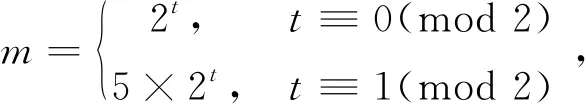
利用式(45),可将式(41)化为
y2≡±(u2m+15v2m)
≡±15v2m(modu2m)
(46)
考虑到2|m时,um≡1(mod 8),u2m≡1(mod 8)。令2s‖vm,结合式(44),则式(46)可化为

(47)

综上,方程(4)仅有解(x,y)=(15,1)。证毕。
最后证推论3。若2|y,则有4|x。令x=4x1,y=2y1,则式(5)可化为
(48)
根据引理6,式(48)给出x1=129,y1=4。此时可得式(5)的解为(x,y)=(516,8)。

y2=un+9vn,n≥0
(49)
根据引理3,有
un+2=258un+1-un,u0=1,u1=129
(50)
vn+2=258vn+1-vn,v0=0,v1=16
(51)

v2n=2unvn
(52)
(53)
u-n=un,v-n=-vn
(54)
un+2km≡(-1)kun(modum)
vn+2km≡(-1)kvn(modum)
(55)
利用式(50) 和式(51),对式(49)取模29,得T=14,且当n≡1,2,3,5,6,8,9,10,12,13(mod 14)时,y2≡12,21,12,14,15,17,8,17,15,14(mod 29)均为模29的平方非剩余,故排除,剩n≡0,4,7,11(mod 14),即n≡0,4,7,11,14,18,21,25(mod 28)。
对式(49)取模43,得T=4,且当n≡2,3(mod 4)时,y2≡42,28(mod 43)均为模43的平方非剩余,故排除n≡7,11,14,18(mod 28),剩n≡0,4,21,25(mod 28),即n≡0,4,21,25,28,32,49,53(mod 56)。
对式(49)取模503, 得T=56,且当n≡25,28,32,49(mod 56)时,y2≡248,502,358,93(mod 503)均为模503的平方非剩余,故排除,剩n≡0,4,21,53(mod 56)。
对式(49)取模4 817,得T=56,且当n≡4,21,53(mod 56)时,y2≡1 644,3 726,3 233(mod 4 817)均为模4 817的平方非剩余,故排除,剩n≡0(mod 56),从而n≡0(mod 14)。
对式(49)取模37,得T=3,且当n≡1,2(mod 3)时,y2≡14,22(mod 37)均为模37的平方非剩余,故排除,剩n≡0(mod 3)。结合n≡0(mod 14),可得n≡0(mod 42)。

(ⅰ)k≡1(mod 3)时,令
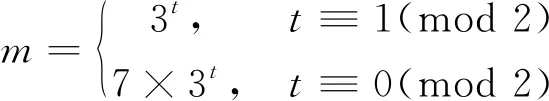
则m≡3(mod 12)。
利用式(55),可将式(49)化为
y2≡±(u2m+9v2m)(modu3m)

(56)

(57)
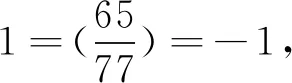
(ⅱ)k≡-1(mod 3)时,令

则m≡9(mod 12)。
利用式(54)和式(55),可将式(49)化为
y2≡±(u2m-9v2m)(modu3m)
(58)

(59)
(60)
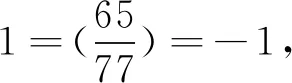
因此n=0。代入式(49)得y=1。此时可得式(5)的解(x,y)=(9,1)。
综上,方程(5)仅有解(x,y)=(9,1)和(516,8)。证毕。
