探究一类电磁学疑难问题

郑金

(凌源市职教中心 辽宁 朝阳 122500)

有关带电小球在匀强磁场中摆动或沿圆弧轨道运动的轨迹是圆弧还是旋轮线的问题，显得非常复杂，需要应用有关的数学知识进行解答.现举例分析.

【例1】如图1所示，摆球质量为m，带正电，电荷量为q，摆长为l，在匀强磁场中的最大摆角为α，为使此摆的周期不受磁场的影响(能正常摆动)，磁感应强度B的值有何限制？

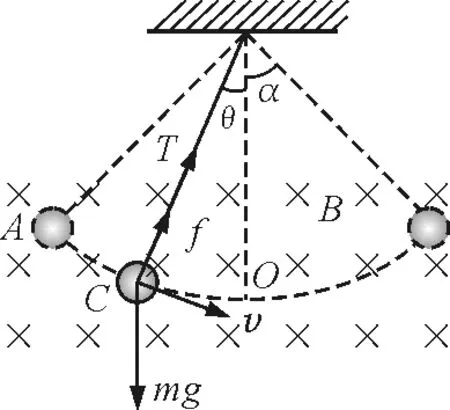
图1

分析:为使摆的周期不受磁场的影响,即能正常摆动，需摆线始终拉直而不松弛，即摆线的拉力T≥0．因此,只需考虑摆球所受洛伦兹力f=qBv并且指向悬点的情形，即摆球由左端A沿圆弧向平衡位置O运动的过程，设某时刻摆角为θ，摆球速度为v，则沿摆线方向由牛顿第二定律有

(1)

对小球从点A到C的过程，由机械能守恒定律有

(2)

联立式(1)、(2)得

(3)

可见，拉力T是关于速度v的一元二次函数，其图像为开口向上的抛物线，若使函数值T≥0，即图像与横轴无交点，则应该使判别式Δ≤0，由此可得

或者由T≥0得

(4)

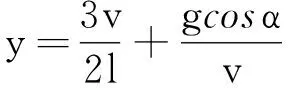
(5)

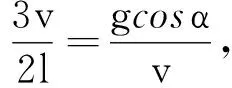
(6)

代入式(4)得

(7)

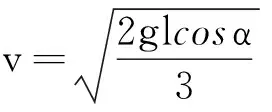
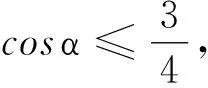
所以，当41°≤α<90°时，摆球沿圆弧运动满足的条件是

那么,当0°<α≤41°时，摆球沿圆弧运动满足的条件是什么呢？

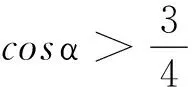
(8)

下面由式(5)和式(8)求y的极值．

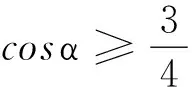
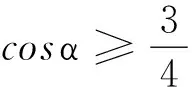
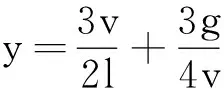
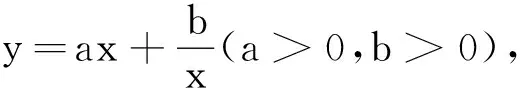
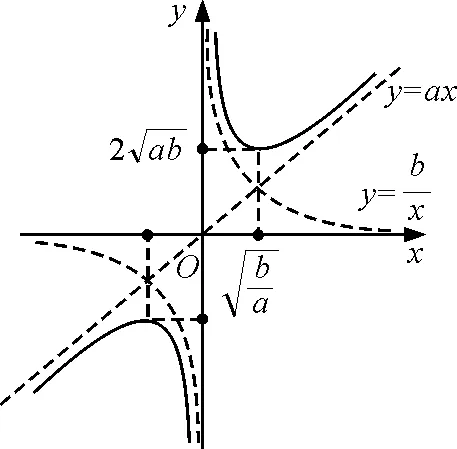
图2

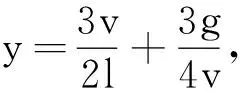
(9)

把式(9)代入式(4)得

(10)

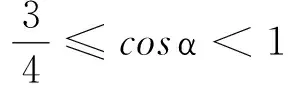
即条件为

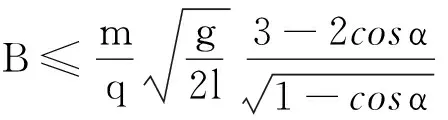
由此可见，当α很小时，磁感应强度可以很大，单摆仍能正常摆动而不致脱离圆弧轨道，这是因为当α角很小时，摆球运动速度将很小，故洛伦兹力很小，同时，重力沿摆线方向的分力很大，则容易满足摆线的拉力不为零．因此,在摆角α较小的条件下，可直接对摆球从端点向最低点运动的过程列方程

两式联立消去v得

利用T≥0可得

在求磁感应强度极值时，也可联立式(1)、(2)消去v得

利用T≥0，可得

整理得

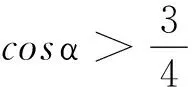
对于该题，常见解法只得出一个结果，即式(7)，而没有对摆角α进行讨论，显得不全面．

由式(7)可知，当α=90°时，得B≤0，这表明，当B≠0时，若带电摆球从水平位置释放，初始阶段将不沿圆弧运动．

【例2】如图3所示，半圆形光滑槽在水平地面上固定不动，匀强磁场沿水平方向垂直于圆面ABC.将质量为m的带电小球自槽口A处由静止释放.小球到达最低点C时，对槽恰好无压力，则小球在以后的运动中对点C的最大压力为

A.0 B.2mgC.4mgD.6mg

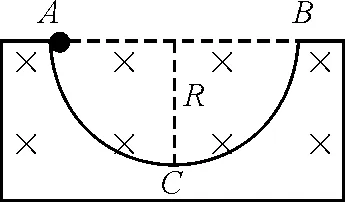
图3

分析：该题与例1相似，则解答方法相似，可直接利用其结果，即由圆周运动的条件式(7)可知，若将带电小球自槽口A处由静止释放，相当于α=90°，在该条件下小球不能做圆周运动，原因是此时得出B≤0，即没有磁场.因此，当有磁场即B≠0时，若带电小球从水平位置释放，初始阶段将不能沿圆弧运动，那么，带电小球将做何种运动呢？小球能否到达最低点C呢？下面进行探讨．

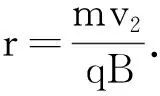
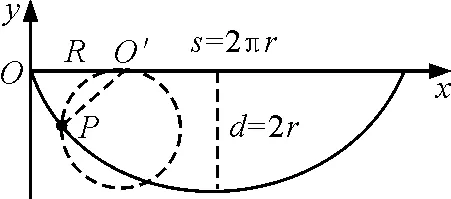
图4

只有半圆的半径足够小，使半圆与旋轮线的交点位于半圆最低点的左侧，小球才能经过半圆的最低点，运动到半圆的右端，接着返回，从右向左运动，此时，洛伦兹力方向背离圆心，当再次运动到最低点时压力达到最大．所以，在一定条件下，小球从左向右运动可以到达半圆形轨道的最低点，但初始阶段的运动轨迹为旋轮线．在保证小球能经过半圆最低点的条件下，对该题解答如下.

当小球从左向右运动经过最低点时，由于小球对槽恰好无压力，则洛伦兹力方向竖直向上，由牛顿第二定律可知，洛伦兹力大小为

若碰撞过程没有机械能损失，则机械能守恒，即

由此得

v2=2gR

因此洛伦兹力大小为f=3mg

由洛伦兹力方向竖直向上和左手定则可知小球带正电，因此，当小球再次返回到最低点时，洛伦兹力方向竖直向下，大小未变，则此时压力最大，由牛顿第二定律可知压力大小为

故选项D正确.

参考文献

1 郭铨．带电摆球在磁场中正常摆动的条件分析．中学物理，1999(3)

2 石长盛．此题应加以讨论．中学物理，2000(9)

3 李池．对一道电磁学题目题设条件的质疑.物理通报，2011(8)