弹簧系统几个难点问题分析
2013-01-11徐正恒
徐正恒
(衡阳县第一中学 湖南 衡阳 421200)
弹簧类问题在高中物理中占有相当重要的地位,且涉及到的物理问题多是一些综合性较强、物理过程又比较复杂的问题,从受力的角度看,弹簧上的弹力是变力;从能量的角度看,弹簧是个储能元件;中学阶段把弹簧看成是不计质量的理想化模型,对其考查主要集中在与其他物体的相互作用及能量转化上,搞清物体的运动情境,特别是弹簧所具有的一些特点,是正确解决这类问题的重要方法.这些问题在力学知识的不同部分和各种不同层次的测试中经常出现,在每年的高考中都有考查.
1 弹簧系统瞬时性分析
高中研究的弹簧都是轻质弹簧(不计弹簧自身的质量,弹簧没有惯性,也不会有动能),不论弹簧处于何种运动状态(静止、匀速或变速),轻质弹簧两端所受的弹力一定等大反向.由弹簧弹力的产生条件可知,只有弹簧两端同时受力时,弹簧才能产生弹力.
证明:以轻质弹簧为对象,设两端受到的弹力分别为F1,F2,根据牛顿第二定律,可得F1+F2=ma,由于m=0,因此F1+F2=0,即F1,F2一定等大反向.
1.1 弹簧两端与物体相连 弹力瞬间不变
如果弹簧两端与物体相连,由于物体有质量、惯性,其位置在瞬间不会发生变化,所以,弹簧的长度在瞬间不会发生变化,则弹簧的弹力在瞬间不变.
弹簧的两端都有其他物体或力的约束,发生形变时,弹力不能由某一值突变为零或由零突变为某一值.
【例1】如图1所示,小球P,Q质量均为m,分别用轻质弹簧b和细线c悬挂在天花板下,再用另一细线d,e与左边的固定墙相连,静止时细线d,e水平,b,c与竖直方向夹角均为θ=37°.下列判断正确的是
A.剪断d瞬间P的加速度大小为0.6g
B.剪断d瞬间P的加速度大小为0.75g
C.剪断e前c的拉力大小为0.8mg
D.剪断e瞬间c的拉力大小为1.25mg
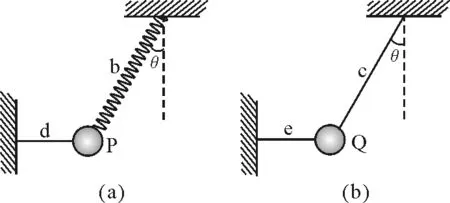
图1
解析:根据平衡条件由拉密定理可得
所以
Fd=0.75mgFb=1.25mg
剪断d瞬间弹簧b对小球的拉力大小和方向都未来得及发生变化,因此,重力和弹簧拉力的合力与剪断前d对P的拉力大小相等,为0.75mg,所以,加速度大小为0.75g,水平向右;剪断e前c的拉力大小为1.25mg,剪断e后沿细线方向上的合力充当向心力,c的拉力大小立即减小到0.8mg,选项C错,所以答案为选项B.
1.2 弹簧一端与其他物体脱离 弹力瞬间为零
弹簧的弹力属于接触力,弹簧两端必须都与其他物体接触才可能有弹力.如果弹簧的一端与其他物体脱离接触,或处于拉伸状态的弹簧突然被剪断,那么,弹簧两端的弹力都将立即变为零.
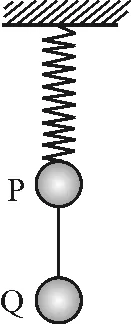
图2
【例2】质量分别为m和2m的小球P,Q用细线相连,P用轻质弹簧悬挂在天花板下,开始系统静止,如图2所示.下列说法中正确的是
A.若突然剪断细线,则剪断瞬间P,Q的加速度大小均为g
B.若突然剪断细线,则剪断瞬间P,Q的加速度大小分别为零和g
C.若突然剪断弹簧,则剪断瞬间P,Q的加速度大小均为g
D.若突然剪断弹簧,则剪断瞬间P,Q的加速度大小分别为3g和零
解析:剪断细线瞬间,细线拉力突然变为零,弹簧对P的拉力仍为3mg,竖直向上,剪断瞬间P的加速度为2g,竖直向上,而Q的加速度为g,竖直向下,选项A,B错;剪断弹簧瞬间,弹簧弹力突然变为零,细线对P,Q的拉力也立即变为零,因此,P,Q的加速度均竖直向下,大小为g.所以,答案为选项C.
2 弹簧系统对称性分析
轻质弹簧一端固定,另一端系一个小球,便组成一个弹簧振子.无论此装置水平放置、倾斜放置还是竖直放置,在忽略摩擦阻力和空气阻力的情况下,弹簧振子的振动都是简谐运动.
简谐运动的特点之一就是对称性.振动过程中,振子在离平衡位置距离相等的对称点,所受回复力、位移、速度、加速度大小及振子动能、弹性势能、机械能等都是相同的,且做周期性变化.
2.1 振动位置的对称性
弹簧振子振动时具有对称性,分析时应注意两点,一是抓住平衡位置,二是运用对称特征.
【例3】如图3(a)所示,劲度系数为κ的轻质弹簧竖直放置,下端固定在水平地面上,一质量为m的小球,从离弹簧上端高h处自由下落,接触弹簧后继续向下运动.若以小球开始下落的位置为原点,竖直向下建立坐标轴Ox,小球的速度v2随x变化的图像如图3(b)所示.其中OA段为直线,AB段是与OA相切于A点的曲线,BC是平滑的曲线,则关于A,B,C三点对应的x坐标及加速度大小,以下关系式正确的是
A.xA=h,aA=g
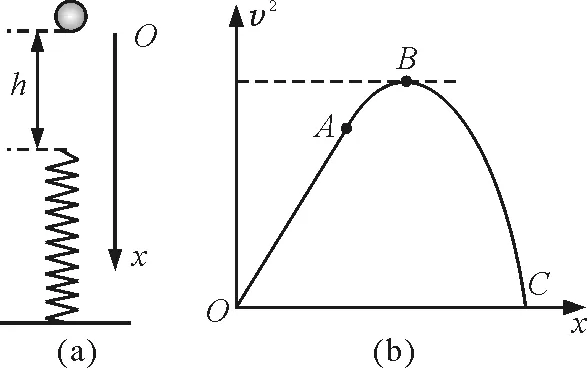
图3
解析:由图3(b)以及公式v2=2gx可知,OA段为直线表示小球做自由落体运动,以后小球在弹簧上做简谐运动至最低点C.A点表示小球刚好接触弹簧,xA=h,aA=g,故选项A正确;B点是平衡位置,满足
κx0=mg
所以有
选项B正确;C点是最低点,根据弹簧振子做简谐运动的对称性可得
选项D正确.所以答案为选项A,B,D.
2.2 物理量变化的对称性
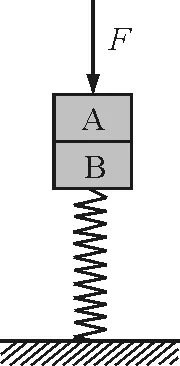
图4
【例4】如图4所示,轻质弹簧的一端固定在地面上,另一端与木块B相连,木块A放在木块B上,两木块质量均为m,在木块A上施有竖直向下的力F,整个装置处于静止状态.
(1)突然将力F撤去,若运动中A,B不分离,则A,B共同运动到最高点时,B对A的弹力有多大?
(2)要使A,B不分离,力F应满足什么条件?
解析:力F撤去后,系统做简谐运动,该运动具有明显的对称性,该题利用最高点与最低点的对称性来求解,会简单得多.
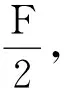
所以,B对A的弹力为
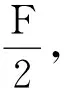
3 弹簧系统多解性分析
对于只有一端有关联物体,另一端固定的弹簧,其运动过程可结合弹簧振子的运动规律去认识,突出过程的周期性、对称性及特殊点的应用.如当弹簧伸长到最长或压缩到最短时,物体的速度最小(为零),弹簧的弹性势能最大,此时,也是关联物的速度方向发生改变的时刻.若关联物与接触面间光滑,当弹簧恢复原长时,物体速度最大,弹性势能为零.若关联物与接触面间粗糙,物体速度最大时,弹力与摩擦力平衡,此时弹簧并没有恢复原长,弹性势能也不为零.若关联物同时处在电磁场中,要注重过程的分析.
两端均有关联物的弹簧,伸长到最长或压缩到最短时,相关联物体的速度一定相同,弹簧具有最大的弹性势能,当弹簧恢复原长时,相关联物体的速度相差最大,弹簧对关联物体的作用力为零.若物体再受阻力时,弹力与阻力相等,物体速度最大.针对此类问题,要立足运动和受力分析,在解题方法上以动量定理、动量守恒定律和动能定理等为首选.
3.1 运动过程的周期性
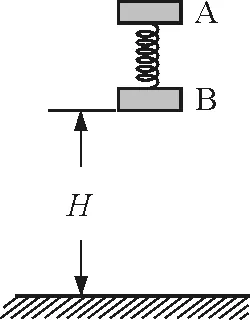
图5
【例5】如图5所示,将质量均为m,厚度不计的两物块A,B用轻质弹簧相连接.第一次只用手托着B物块于H高处,A在弹簧弹力的作用下处于静止,现将弹簧锁定,此时弹簧的弹性势能(与弹簧形变量大小有关)为Ep,现由静止释放A,B,B物块着地后速度立即变为零,同时弹簧锁定解除,在随后的过程中B物块恰能离开地面但不继续上升.第二次用手拿着A,B两物块,使得弹簧竖直并处于原长状态,此时物块B离地面的距离也为H,然后由静止同时释放A,B,B物块着地后速度同样立即变为零.不计空气阻力,求:
(1)第一次释放A,B后,A上升至弹簧恢复原长时的速度v1;
(2)第二次释放A,B后,B刚要离地面时A的速度v2.
解析:设弹簧原长为L,则整个过程各状态如图6所示.

图6
(1)设物体下落H高度时的速度为v0
(1)
弹簧被锁定和物块B刚被提起时,弹簧的形变量为x,根据平衡条件
mg=κx
(2)
从B着地到A到达最高点,对弹簧和物块A,根据机械能守恒定律有
(3)
设弹簧恢复原长时,物块A的速度为v1,则
(4)
由式(1)~(4)得
(5)
(2)从B着地到刚被提起,对弹簧和物块A
(6)
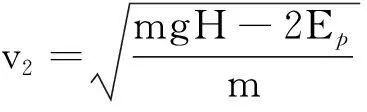
(7)
3.2 物理量变化多值性
【例6】如图7所示,水平面上的轻质弹簧一端与物体相连,另一端固定在墙上的P点,已知物体的质量为m,物体与水平面间的动摩擦因数μ,弹簧的劲度系数κ.现用力拉物体,使弹簧从处于自然状态的O点由静止开始缓慢向左移动一段距离,这时弹簧具有弹性势能Ep.撤去外力后,物体在O点两侧往复运动的过程中
A.在整个运动过程中,物体第一次回到O点时速度不是最大
B.在整个运动过程中,物体第一次回到O点时速度最大
D.在物体第一次向右运动的过程中,速度相等的位置有两个
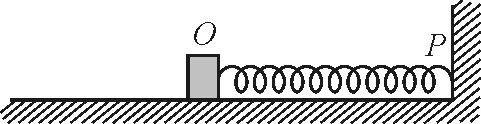
图7
解析:物体振动的平衡位置满足
κx0=μmg

在物体第一次向右运动的过程中,速度相等的位置有两个,分别在平衡位置x0两侧相对平衡位置对称.故答案为选项A,D.
综上所述,弹簧问题不仅能很好地考查学生分析物理过程,理清物理思路,建立物理图景的能力,而且还能考查学生的分析综合能力、迁移能力、处理实际问题的能力,对培养学生物理思维品质和挖掘学生学习潜能都有好处.
