单摆周期问题的归纳与深化

单摆在摆角很小时的振动是简谐振动的典型实例,其周期公式为根据这一公式可知,决定单摆周期的因素有两个,即摆长L和单摆所处情况下的加速度g。在中学课本中,关于g的概念并未给出一般性的定义,这就给同学们求解复杂情况(如在超重、失重、系统加速、复合场中等)下单摆的周期问题带来一定困难。下面结合单摆振动的具体实例分析单摆周期的求法。

一、确定单摆的平衡位置

求单摆的周期,确定其平衡位置是关键的一步。单摆振动时,所在系统(单摆本身)运动情况的复杂性决定了单摆平衡位置的复杂性。

1.在静止或匀速运动的体系(惯性系)中的单摆如图1～5所示。

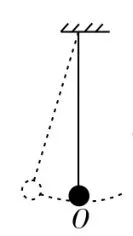
图1

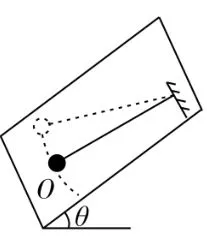
图2

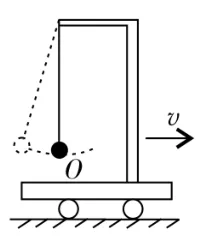
图3

图4

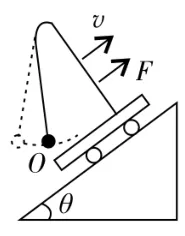
图5

如图1～5中所示单摆在不振动时,摆球总是相对悬点静止在O点,若让其振动,摆球离开平衡位置,就要受到回复力作用(总是指向O点),可见O点就是其摆动的平衡位置。摆球静止在O点时,所受的合外力为零,回复力也为零;摆球在振动过程中经过O点时,其回复力仍为零,但因摆球沿圆弧运动,故它所受的外力不为零。因此,在惯性系中,单摆的平衡位置就是摆球不振动时相对于悬点静止的位置,摆球在此位置时所受回复力一定为零。

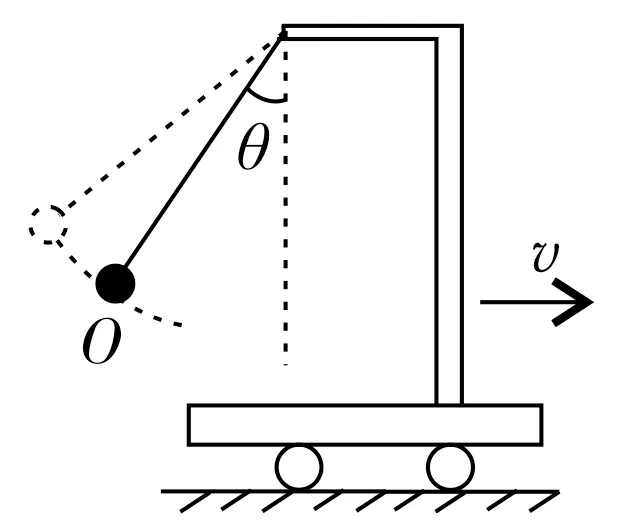
图6

2.在加速运动的体系(非惯性系)中。

如图6所示,在水平向右加速运动的小车上,当摆球不振动(相对车静止)时,悬线必然要偏离竖直方向一个角度θ,而相对静止在O点,此时摆球处于相对稳定状态。此时,若让摆球偏离O点一个较小角度,摆球就要来回摆动(总想回到位置O),因此,这一相对悬点稳定的位置O就是单摆的平衡位置,摆球在此位置时所受回复力为零。

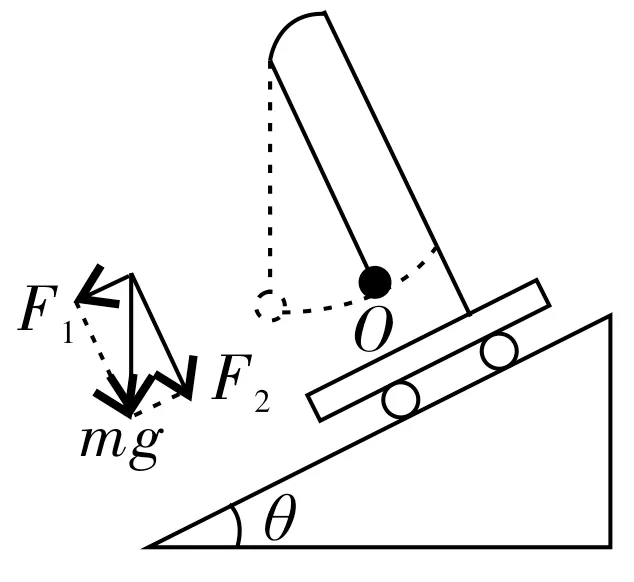
图7

如图7所示,在沿光滑斜面加速下滑的小车上,单摆和小车一同加速下滑,在摆线和斜面垂直(摆球处于O点)时,摆球处于相对稳定状态,这个位置O就是单摆的平衡位置,摆球在此位置时所受回复力为零,但合外力不为零。

根据以上分析可知,单摆的平衡位置就是单摆不振动时摆球相对悬点静止的位置,摆球处于平衡位置的动力学特点是所受合外力不一定为零,但回复力一定为零。因此,不管是在惯性系中还是在非惯性系中,要找单摆的平衡位置,只要找出摆球不振动时相对悬点静止的位置就可以了。

二、求单摆周期的方法

如图7所示,单摆和小车在沿倾角为θ的光滑斜面下滑的过程中,如何求单摆摆动的周期呢? 部分同学在求解此题时容易误认为摆长和重力加速度都未改变,所以周期不变。实际上g值虽然未变,却存在效果上相当于g值改变的因素。从图中可以看出,单摆和小车在沿斜面下滑的加速运动中,单摆系统的加速度是由重力的分力F1=mgsinθ产生的,它起不到回复力的作用,所以也就影响不了单摆的振动周期。摆球能相对小车发生振动是由重力的另一个分量F2=mgcosθ引起的,即相当于有mgcosθ的重力作用在摆球上,因此这时单摆的周期可见,求单摆的周期关键在于求作用在摆球上的相当于重力的那个力F。

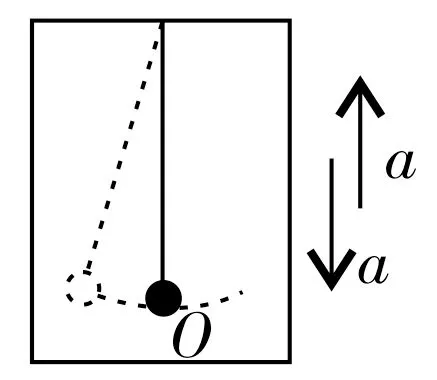
图8

如图8所示,升降机在加速上升时,相当于重力的力F=mg+ma,单摆的周期;升