大摆角耦合摆的运动规律的数值分析
2017-04-01高伟
高 伟
(平凉市第一中学 甘肃 平凉 744000)
大摆角耦合摆的运动规律的数值分析
高 伟
(平凉市第一中学 甘肃 平凉 744000)
基于并联耦合摆理论模型, 利用数值方法研究了在较大摆角情况下并联耦合摆的运动规律.通过分析该系统在较大摆角时摆球的相轨迹图像和庞加莱截面图像,可发现并联耦合摆在较大摆角下的运动是准周期运动,该规律与摆球质量是否相同无关.
耦合摆 相图 庞加莱截面 准周期运动
1 引言
自然界中普遍存在着相互作用的振动系统,如电学中电容和电感耦合起来的振荡回路[1]、固体晶格中相邻原子的振动模式[2]以及光子和声子耦合场[3]等.相互作用使振动系统呈现丰富的动力学行为.因此,无论从工程领域还是基础科学领域的研究需要来讲,对有相互作用的振动系统的运动规律进行研究是非常必要的. 耦合摆作为一种通过力的相互作用从而实现振动系统相互作用的装置,具有结构简单、演示效果直观的特点.对于耦合摆运动规律的研究,通常为了理论研究方便,很多教科书和研究者往往分析了小摆角情况下的运动规律[1,4,5].结果表明,在小摆角下,通常并联耦合摆的各摆球做周期运动.本文利用数值方法,研究的是在较大摆角振幅下并联耦合摆的运动规律.
2 并联耦合摆运动的动力学模型
本文所研究的并联耦合摆模型如图1所示.两个摆球分别用摆线拴在点(-x0,0)和点(x0,0)上,摆长相等(均为L且不可伸缩),摆球之间用轻质的弹簧连接(且保持直线状态),当它们自然下垂时,弹簧也恰好处于自然长度的状态.在初始状态,设摆球2静止,对摆球1进行水平一击,来研究它们其后的动力学行为.
只考虑两个摆球各自的切向运动,用两个摆角θ1和θ2描述它们的运动.先写出约束关系
x1=-x0+Lsinθ1y1=-Lcosθ1
(1)
x2=x0+Lsinθ2y2=-Lcosθ2
(2)
摆球1和摆球2的切向单位矢量分别是
n1=(cosθ1,sinθ1)
(3)
n2=(cosθ2,sinθ2)
(4)
从摆球1指向摆球2的单位矢量(也是弹性力的单位矢量)为
(5)
其中弹簧的瞬时长度
(6)
根据以上关系,可以求得弹簧对摆球1的切向力为
(7)
弹簧对摆球2的切向力为
(8)
于是,两个摆球的运动方程为[6]
(9)
3 并联耦合摆的准周期运动
式(9)是一个紧密耦合的二阶非线性常微分方程,没有普通的解析解.如果要解析研究式(9)所描述的运动规律,只有假定两个摆角θ1和θ2的振幅非常小(一般小于0.08弧度),这样可以把式(9)简化为线性方程组[4,5].利用线性常微分方程的一般解法,比较容易得到两个摆球各自的运动规律.但是,如果要研究任意摆角振幅,研究式(9)所描述的运动规律,必须进行数值计算.图2是通过利用四阶龙格-库塔法数值求解式(9)得到的两个摆球在运动60 s时间段内的相轨迹图像,其中系统参数为g=9.8,m1=0.2,m2=0.2,L=1,k=0.5.初始条件:摆球1为{0,1.9},摆球2为{0,0}.从图2可以看出,两个摆球的相轨迹都呈现出明显的特点:
(1)比较一般的周期运动或者多周期运动的相轨迹,图2呈现出比较复杂的图像;
(2)但比较更复杂的混沌运动的相轨线,图2又表现出明显的规律性,因此我们猜测两个摆球的运动应该是介于周期运动和混沌运动之间的准周期运动.



图2 两个摆球的相轨迹图
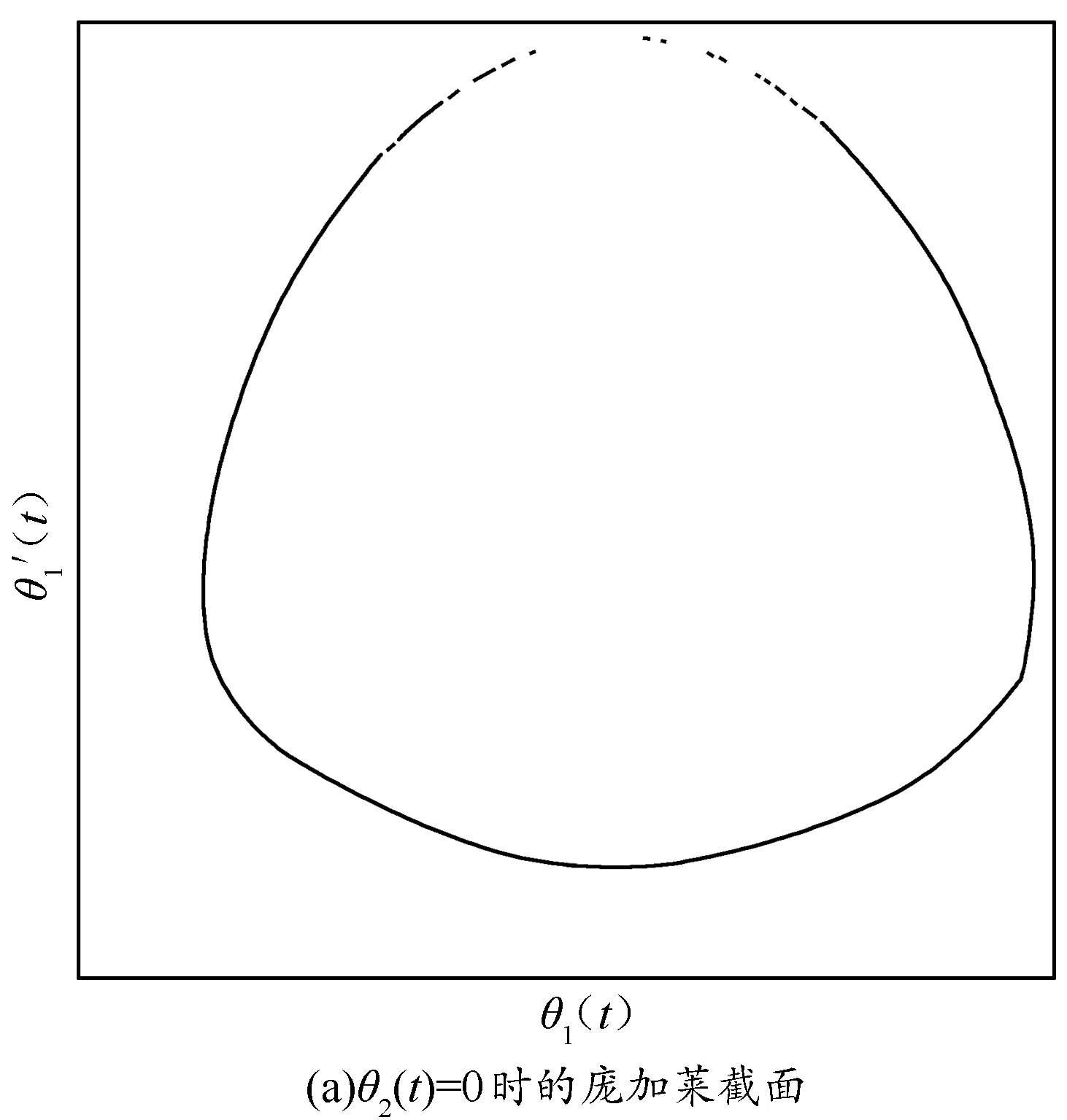

图3 摆球1在不同情况下的庞加莱截面图

4 摆球质量对并联耦合摆运动的影响
前面研究的是在两个摆球质量相同时的情况.接下来,考虑两个摆球的质量如果不同,对耦合摆的运动有什么影响.参数改为g=9.8,m1=0.1,m2=0.2,L=1,k=0.5,两个摆球的相轨迹图和庞加莱截面如图5~7所示.
从图5可以看出,如果两个摆球的质量不同,摆球1和摆球2的相轨迹将发生明显地改变:(1)两个摆球的相轨迹都呈现出明显地左右不对称性;(2)与图2不同,两个小球的相轨迹存在的区间发生明显的差别,比如摆球2的相轨迹纵坐标范围从以前的[-1.6,1.6]变成[-1.2,1.2],横坐标范围从以前的[-0.5,0.5]变成[-0.4,0.4].这表明,在耦合摆运动中,质量大的摆球获得的机械能反倒小于质量小的摆球.从图6和图7可以看出,庞加莱截面得到的图像仍然是闭合的曲线,所以,运动依然是准周期运动.可见,即使两个摆球质量不同,也未能改变并联耦合摆总的运动特点.

图5 两个摆球质量分别为m1=0.1,m2=0.2时的相轨迹图

图6 摆球1在质量为m1=0.1,m2=0.2时的庞加莱截面图

图7 摆球2在质量为m1=0.1,m2=0.2时的庞加莱截面图
5 结论
本文通过理论推导,得出了并联耦合摆的动力学方程.为了对各个摆球的运动特点进行分析,通过利用四阶龙格-库塔数值积分的方法作出了它的相轨迹图像和庞加莱截面.从各个摆球运动的相轨迹图像和庞加莱截面可以看出,在大角度振幅下,并联耦合摆两个摆球的运动是准周期运动.我们还发现,如果两个摆球的质量不一样,各个摆球相轨迹会发生变化,但准周期的运动规律不会改变.
1 姚盛伟,徐平,Jacques Tabuteau.耦合摆特性模拟及振动耦合现象演示.大学物理,2012,31(4): 28~32
2 黄昆,韩汝琦.固体物理学. 北京:高等教育出版社, 1988
3 郑力明,王发强,刘颂豪.光声互作用模型中的Pancharatnam相位. 物理学报,2009,58(5):2 884~2 887
4 周衍柏.理论力学教程.北京:高等教出版社,2009
5 龚善初.失调耦合摆振动分析.大学物理,2005,24(8):21~24
6 董键.Mathematica与大学物理计算.北京:清华大学出版社,2010
7 刘秉正,彭建华.非线性动力学.北京:高等教育出版社, 2005
8 陆同兴,张季谦.非线性物理概论.合肥:中国科学技术大学出版社,2010
Numerical Analysis on the Motion Law of Coupled Pendulum at Larger Oscillation Angles
Gao Wei
(NO.1 Middle School of Pingliang, Pingliang, Gansu 744000)
Based on the theoretical model about the motion of the coupled pendulum in parallel, the motions of the coupled pendulums in larger swing angles are investigated by using numerical methods. The phase diagrams and the poincare sections of the coupled pendulums are analyzed. The numerical results show that the motions of the coupled pendulums in larger swing angles are quasi-periodic motions.
coupled pendulum; phase diagram; poincare section; quasi-periodic motion
高伟(1981- ),男,中教一级,主要从事中学物理教学及理论物理方面的研究工作.
2016-10-25)
