电磁感应中的含容电路分析

黄鑑 杨军 唐齐林

(成都七中 四川 成都 610041)

1 理想模型

如图1，在无限长的光滑竖直导轨区域内，有垂直于纸面的匀强磁场.导体棒AB(电阻忽略不计)与导轨接触良好，当其由静止沿导轨自由下滑时，整个电路便会通有稳恒直流电.下面就这一物理模型进行运动学和能量学两个方面的分析.

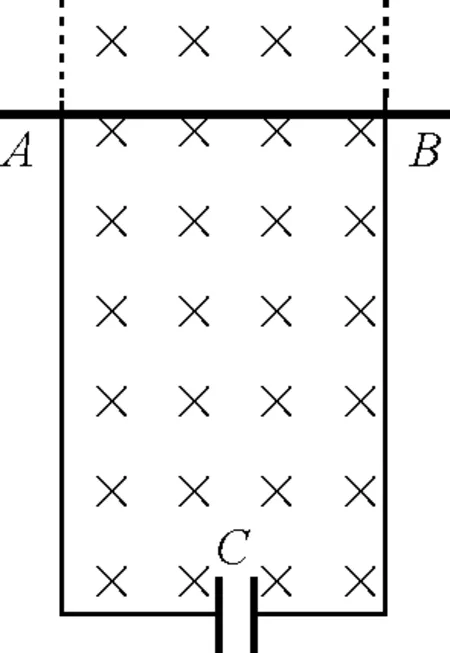
图1

(1)运动学方面

我们先作宏观分析，导体棒加速下滑时，由于速度增加，会导致感应电动势增加，从而使得电容器两极板电荷量增加，电荷在电路中定向移动.由于电路中电荷的定向移动，电路中便形成电流.同时，电流的存在又会导致棒AB受到安培力的作用，安培力阻碍其加速下滑.这些因素互相联系，相互制约,此电流为稳恒电流.对此,我们可以这样理解，整个过程如图2所示.

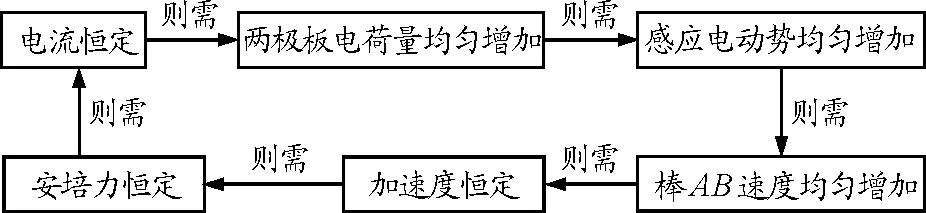
图2

下面我们定量地分析一下导体棒的运动过程.设棒AB质量为m，导轨宽为l，磁感应强度为B.对于电容器有

Q=CU

所以

ΔQ=CΔU

这里的U为感应电动势，有

U=Blv

所以

ΔU=BlΔv

ΔQ=CΔU=CBlΔv

又

对棒AB受力分析有

mg-BIl=ma

即

mg-BCBlal=ma

所以

由此可以看出，对于任意的m,B,C,l都有一个恒定的a.即棒AB都能做匀加速运动，电路都能通有稳恒直流电.

(2)能量方面

导体棒下滑时，能量必须守恒.那么,重力势能在转化为动能的同时还转化为什么能量呢?毫无疑问是电能——电容器储存的电能.我们知道重力势能的改变量在数值上与重力做功是相等的,而mg=ma+BIl，根据动能定理，合外力ma做的功在数值上与动能增量相同.因此，只需要研究安培力BIl做的功在数值上是否与电容器所储的电能相等即可.

下面定量计算安培力所做的功，即

而电容器储能公式为

即分别为电容器所储能量与将所储电荷量从一极板移到另一极板所做的功.因为Q=It，所以

所以

W安=WC

说明电容器储能与力BIl做的功在数值上是相等的,进一步说明了这一过程满足能量守恒规律.

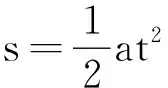
2 实际模型

将此模型稍作改动,或者说更现实化,如图3.

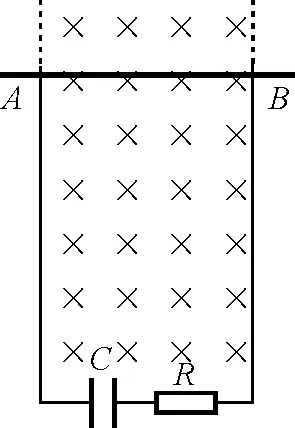
图3

棒AB不能一开始就做匀加速直线运动,系统需要经过一个变加速过程才能达到稳定.稳定后,棒AB做匀加速直线运动,电路通稳恒电流.其原因在于电路中电流的产生仍然在于电容器的充电、感应电动势的增加.所以,电路最后的稳定电流、加速度等在计算时仍与前面方法相同，且与R无关.而R的存在只是影响到系统何时稳定及能量分配的问题.因为，我们可以求出一个电流I,它虽然与R无关，但R产生一个电压降IR，因此,在稳定前,感应电动势Blv必须先达到R的电压需求IR，之后,方可稳定.这便是R对系统何时稳定的影响.下面我们研究一下能量分配，重力势能转化为动能、焦耳热以及电容器所储电能.由于系统需要一个稳定过程，所以，我们计算其稳定后的功率问题,与前面同理，只需研究BIl做功功率在数值是否与焦耳热产热功率和电热器储能功率之和相等即可.

P安=BIlv=B2l2Cav

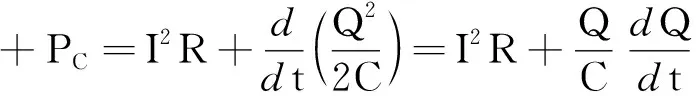
由于电容器两端电压为

U=Blv-IR

所以

Q=Blv-IRC

且

所以

P焦+PC=I2R+Blc-IRI=

BlvI=B2l2Cav

可得

P焦+PC=P安

能量守恒，进一步说明了对此模型分析的正确性.从能量角度说，虽然I与R无关，但P焦=I2R与R有关，R的大小影响到P焦的大小.因此,系统要达到稳定，棒AB必须要有一个适当的初速度，从而，使得重力势能的改变率足够大，以满足P焦.这也说明了系统需要一个稳定过程.当然，以上情况均是在电容器完好的条件下进行，同时也均是一些理想化的情形，采用了一些理想化的思维方式.

近年来，越来越多的高考和竞赛题涉及到此类物理模型，旨在考查学生对有电容器的电路中产生电流的根本原因的理解，以及对物理模型全方位、多因素的分析能力.