“动态”立体几何题解法剖析

● (江苏教育学院附属高级中学 江苏南京 210036)

立体几何是中学数学传统的主体内容之一，也是当前高考命题的一个热点内容.它不仅能考查学生的空间想象力，还能更好地体现学生思维的深刻性和灵活度.随着新课改地不断深入，立体几何以柱体和锥体为载体来考查立体几何中的重要内容，譬如线线、线面与面面的位置关系.“动态”探索性问题是近几年高考立体几何命题的新亮点，以此来考查立体几何问题中的证明和计算.有时学生对此类问题感到措手不及，因此，教师在教学中非常有必要对知识进行活化，引导学生通过观察、比较、联想等思维过程，把新的立体几何问题纳入到原有的认知结构中，用熟悉的平面几何知识、代数方法等进行解答.笔者对求解立体几何问题总结为“八字方针”，即“截、移、割、补、展、折、射、转”，仅供大家参考.

1 “截”

“截”是指在空间图形中作截面，求截面的面积、截面与指定平面所成的角、截面将多面体分割成几部分的体积等问题，从而把问题转化为较容易的(或特殊的)问题加以求解.

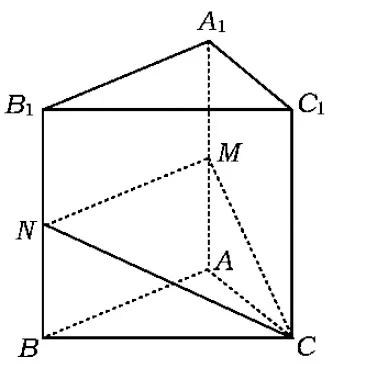
图1

图2

解当交线MN在侧面A1B内(或与A1B1重合)时，

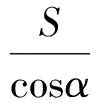
当MN在底面A1B1C1内时，

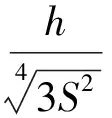
因此

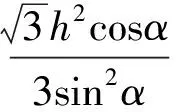
点评截面问题是立体几何中的常见题型，由于截面的动态性，使截得结果也具有一定可变性.

2 “移”

“移”是指先将某图形平移到适当位置，使不在同一平面上的元素集中到一个平面上，再利用平面几何知识进行研究，实现立体问题向平面问题的转化.

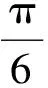
点评通过图形位置的适当平移，可以实现空间图形向平面图形的迅速转化，让学生真实地感受到立体几何动感的一面.

3 “割”

“割”是指当所呈现的几何体较复杂、有关的计算公式无法直接运用或计算较繁时，可以适当地分割几何体，化整为零，从而迅速破解.

例3将半径为1的4个钢球完全装入形状为正四面体的容器中，这个正四面体高的最小值是

( )

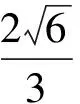
(2005年全国数学高考理科试题Ⅱ)

点评近几年，高考立体几何题出现一些求不规则几何体的体积问题或利用体积转化来求其他的几何量.处理这一问题的常用方法是“割补法”，再用体积公式计算即可，它是化归思想在立体几何中的应用.

4 “补”

“补”是指根据解题的需要将几何题补出适当的部分，变到比较熟悉的或者比较简单的几何体中，再进行求解.“补形”不但能带来计算上的简便，有时甚至是问题得以解决的唯一途径.

例4如图3,已知三棱锥P-ABC的3条侧棱PA，PB，PC两两垂直，且长度分别为3，4，5，试求该三棱锥外接球的表面积.

分析将3条侧棱两两垂直的三棱锥P-ABC补成一个长方体，两两垂直的3条侧棱就是长方体的长、宽、高，则该长方体的对角线长就是三棱锥P-ABC的外接球的直径.设其直径为2R，则

故

点评在解题中常遇到3条侧棱相互垂直的三棱锥，通常将它补成长方体，易于求解.特别地，若三棱锥的3个侧棱相互垂直且相等，则可将它补成正方体.

图3

图4

5 “展”

“展”是指展开空间图形，它是将立体几何问题转化为平面几何问题的常用方法，应用此法可以化折为直、化曲为直.一般用于求选择路径问题、几何中的最值问题等.

例5有一根长3π cm，底面半径为1 cm的圆柱形铁管，用一根铁丝在铁管上缠绕2圈，并使铁丝的2个端点落在同一母线的2个端点处，则铁丝的最短长度是

( )

A.2π B.3π C.4π D.5π

点评展开图着重解决的是侧面及最短距离等问题.在折叠与展开的问题中，应重视前后图形的对比，注意空间图形的棱、侧棱、母线等分别是平面图形中的哪些量，从而进行相关几何量的计算.

6 “折”

“折”是指将平面图形折叠成立体图形.要认清平面图形中各已知条件的相互关系及其本质，平面图形折叠成立体图形后，要注意哪些量发生了变化，哪些量未发生变化，这些未变化的已知条件都是分析问题和解决问题的依据.

例6如图5，在边长为2的正方形SG1G2G3中，E,F分别是G1G2，G2G3的中点，D是EF的中点，现在沿SE,SF及EF把这个正方体折叠成一个四面体，且点G1,G2,G3重合，重合后的点记为G，求四面体G-SEF的体积．

分析若先求出点G到平面SEF的距离，然后利用三棱锥的体积公式求解，则比较麻烦.若注意到三棱锥G-SEF的体积与三棱锥S-GEF的体积相等，即VG-SEF=VS-GEF,则较容易得到解决.

图5

图6

由题意知

SG⊥GE,SG⊥GF，且GE∩GF=G，

因此SG⊥面GEF．又由正方形的棱长为2，易知

于是四面体G-SEF的体积为

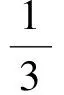
点评把平面图形翻折成立体图形的有关计算问题，易将翻折前的点、线、面之间的位置关系和数量关系误用到翻折后.在解题时,必须抓住在翻折过程中点、线、面之间的位置关系和数量关系，分清变量和不变量，特别要抓住不变量，有时它就是解题的关键.

7 “射”

“射”是指利用射影(投影)的方法将空间图形的若干元素集中到同一平面内，再利用平面图形的相关性质求解.

例7正四面体的棱长为1，棱AB∥平面α，则正四面体上的所有点在平面α内的射影构成的图形面积的取值范围是________.

分析正四面体绕AB旋转，当CD∥平面α时,CD在平面内的射影最长，记为GH，面积也最大，则

点评“动态”立体几何问题是高考立体几何考查的最具有创新意识的题型，而“射影”是其很好的一个素材.通过“射影”把立体几何问题转化为平面几何问题求解.

8 “转”

“转”是指将某些空间图形转化为平面图形或把某些图形适当地转换一些角度进行求解.

( )

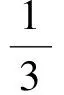
A.直线 B.椭圆

C.双曲线 D.抛物线

图7

所以

故在平面ACC1A1内，动点M到定点A的距离与到定直线CC1的距离的比是一个大于1的常数，点M的轨迹是双曲线.

点评动点轨迹问题是高考立体几何“动态”问题最为新颖的一种命题形式，它体现在立体几何与解析几何的知识交汇处命题.对于此类问题通常可联想到解析几何中有关轨迹定义(譬如圆、圆锥曲线、角平分线、球等)，把条件作适当地转换，将立体几何问题转化为平面解析几何中的轨迹问题求解.

立体几何是培养学生空间想象能力的数学分支，培养学生的识图、想图、画图的能力；培养学生文字语言、符号语言、图形语言的转化能力等.近几年新颖的立体几何问题已成为高考试题新亮点.解决此类问题的关键是准确地把握立体几何中的截、移、割、补、展、折、射、转这8种变换策略，从变化的角度分析问题，便可得到解决问题的有效方法.