构造多种模型证明Shapiro不等式

● (鄞州区古林职业高级中学 浙江宁波 315177)

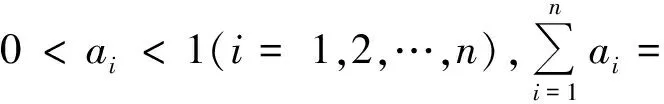
这个不等式称为Shapiro不等式,很多文献对此都有所介绍.本文从不同角度思考可以得到不同的证法.

1 构造函数模型

引理1函数f(x)定义在区间上,若f′(x)是增函数,则对于xi∈I(i=1,2,…,n),都有

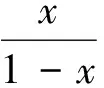
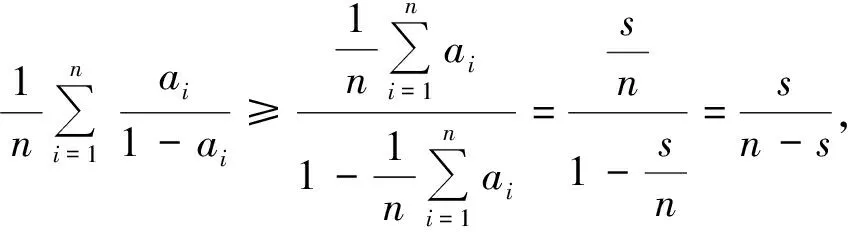
即

评析此方法灵活地利用了一元连续函数的性质所给出的定理,思路通畅、步骤简便,使有些难度较大的不等式问题变得简单,也加深了对函数思想和函数方法的理解,为发现不等式、解决不等式问题开辟了一条途径.

2 构造概率模型

引理2(Cauchy-Schwarz不等式)在概率空间(Ω,F,P)中,设E(X)表示随机变量的X的数学期望,对任意的随机变量ζ和η,当Eζ2和Eη2存在时,E(ζη)必存在,且|E(ζη)|2≤Eζ2·Eη2,当且仅当P(η=t0ζ)=1时,等号成立(t0是某一常数).

证法2注意到

则所证不等式等价于

即

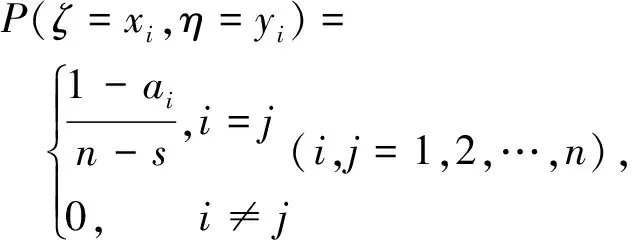
则边际概率分布分别为

又由

|E(ζη)|2≤Eζ2·Eη2,

得

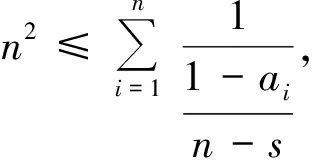
即

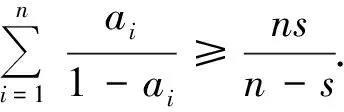
评析用概率方法证明不等式,并非通用的解法,关键是根据不等式特点构造适当的概率模型.此不等式的概率统计意义是2个随机变量乘积的数学期望的平方小于等于2个随机变量二阶矩的乘积.

3 构造数列模型

证法3

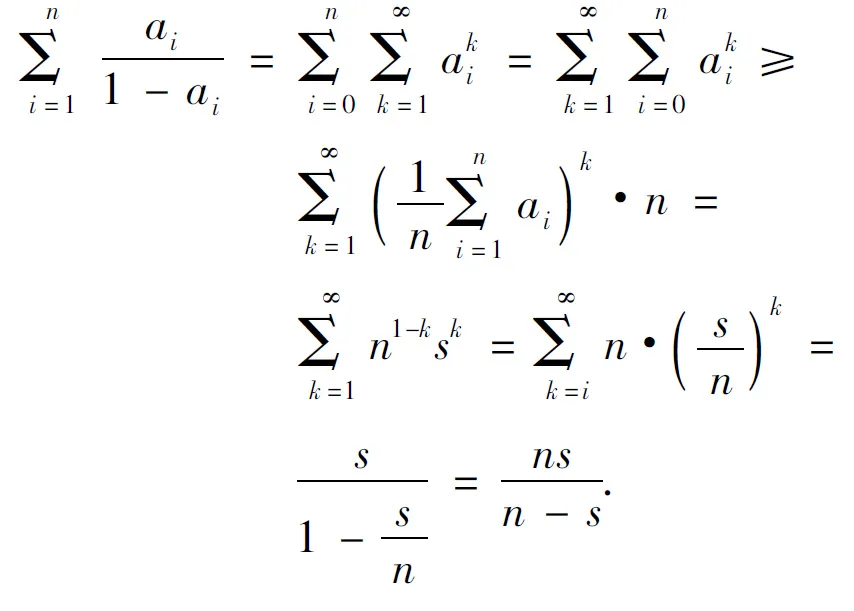
4 构造向量模型

证法4构造向量

则

|n|=a1(1-a1)+a2(1-a2)+…+an(1-an)=

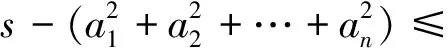
因此

(m·n)2=(a1+a2+…+an)2=s2，

从而

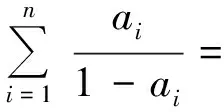
评析构造向量的重点和难点是根据其结构特点,构造2个恰当的向量.

5 构造几何模型

5.1 构造n维空间的距离公式

在n维空间中，点P(x1,x2,…,xn)到平面∏：A1X1+A2X2+…+AnXn+K=0(Ai∈R,K∈R,i=1,2,…,n)的距离为

点P到平面∏上任意点Q(y1,y2,…,yn)的距离为

d2=d(P,Q)=

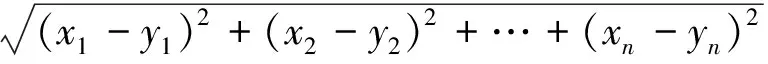
利用d1≤d2的基本关系即可证明.

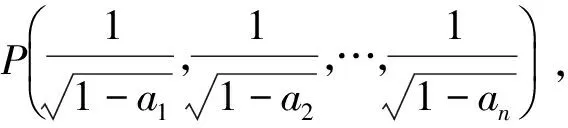
则点O(0,0,0)∈∏.由

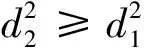
得

变形得

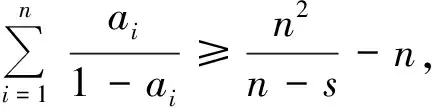
即

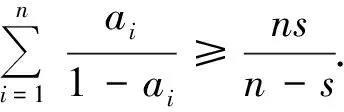
5.2 构造质点系重心法

利用质点系重心法证明不等式的步骤如下:

(1)选取合适的曲线y=f(x),并画出曲线在规定范围内的图形.

(3)计算质点系Ai(xi,yi)的重心坐标

(mi是第i个质点的质量,i=1,2,…,n).

图1

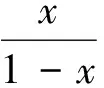
|MG|≥|MN|,

则

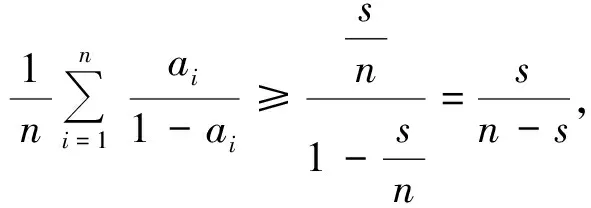
即

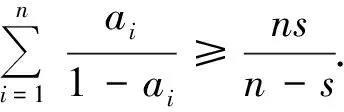
评析从数形结合思想考虑,充分挖掘出不等式的几何背景,分别利用空间距离公式和质点系重心法建立不等式的2种几何模型,利用几何图形的不等性质,使原不等式较易得到证明.

以上从6个不同的角度来思考Shapiro不等式的证法,函数思想一直是高中数学的重要内容和思想方法.概率和向量是新课程中增加的内容,这在一定程度上拓宽了解题思路,对培养学生的创造性思维大有裨益.

[1] 匡继昌.常用不等式[M].3版.济南:山东科学技术出版社,2004:182.

[2] 叶留青,贾长虹.一元连续函数的一个性质定理及其应用[J].焦作师范高等专科学校学报,2009,25(2):71-75.

[3] 王盛刚,张海河.用质点系重心法证明不等式的尝试[J].高等函授学报,2000,13(1):58-64.