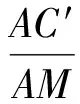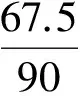一个几何概率试题的题源探究

● (惠安高级中学 福建惠安 362100)

1 题目

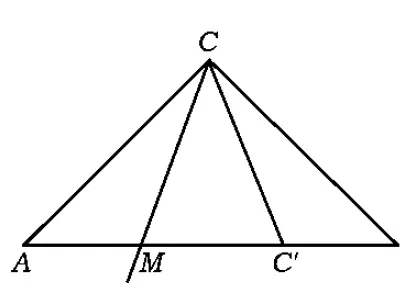
(2009年福建省数学高考文科试题)

解如图1，另一端点B只能在优弧上运动，因此所求概率为

图1

图2

2 题源

2.1 源于历史名题

初看此题以为是数学史上的一个经典的悖论——贝特朗悖论，其实这是一个根据贝特朗悖论改编的题目.贝特朗悖论：“在半径为1的圆周上任取两点，连成一条弦，问弦长超过其内接正三角形的边长的概率是多少?”

从不同方向考虑这道试题，可得不同结果：

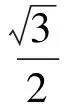
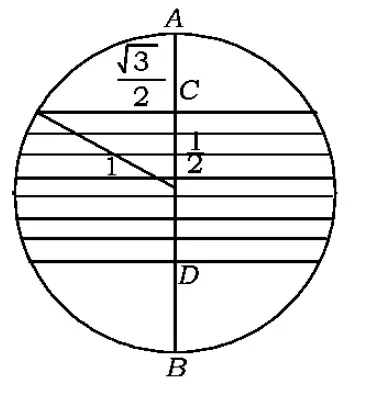
图3

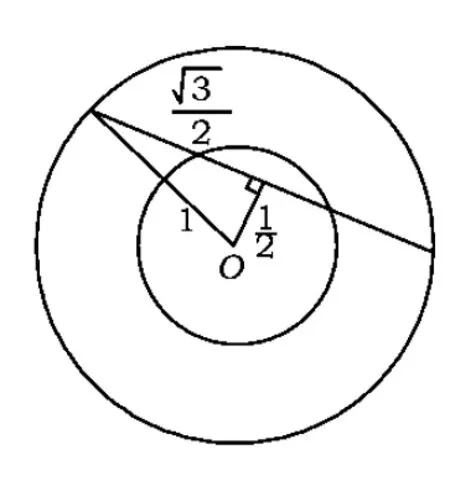
图4

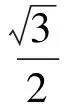
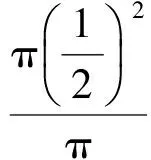
这导致同一事件有不同概率，因此为悖论.

同一问题有3种不同的答案，原因在于取弦时采用不同的等可能性假设!解法1假设端点在圆周上是均匀分布的；解法2假设弦中点在直径上是均匀分布的；解法3是假设弦的中点在圆内是均匀分布的.这3种答案是针对3种不同的随机试验，对于各自的随机试验而言，它们都是正确的.因此在使用术语“随机”、“等可能”、“均匀分布”等时，应明确指明其含义，这又因试验而异.

几何概率是19世纪末新发展起来的一门学科，它使得很多概率问题的解决变得简单.然而在1899年，法国学者贝特朗提出了所谓“贝特朗悖论”，矛头直指几何概率概念本身.悖论提出后，在数学界引起了很大震动，促使数学家理性反思概率论的基础理论.1932年，这个问题才由前苏联的数学家柯尔莫哥洛夫解决，他在其经典的著作《概率论基础》中建立了在测度论的基础上的概率论公理系统，从而把概率论建立在完全严格的数学基础之上.

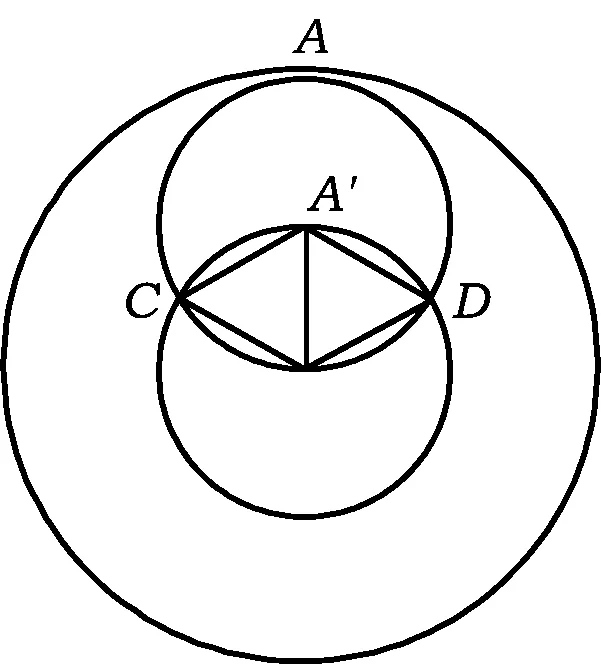
图5

2.2 源于课本

本题也可以说是源于高中教材(苏教版)的必修3第102页中的例题3：

在等腰直角三角形ABC中，在斜边AB上任取一点M，求AM小于AC的概率.

因为点M椭机地落在线段AB上，当点M位于图6中的线段AC′上时，AM

教科书第104页习题7.3第6题(阅读题)将本节例3改为：如图7，在等腰直角三角形ABC中，过直角顶点C在∠ACB内部任作一条射线CM,与线段AB交于点M，求AM

图6

图7

上述2个问题的设计与2009年福建省数学高考文科试题第14题的设计有着异曲同工之妙.2个问题都有着一样的背景，本质都是求解AM

[1] 冯变英，王平.贝特朗悖论与概率论的公理化[J].运城学院学报，2008,26(2):7-8.

[2] 马恩林.几何概率中的贝特朗悖论[J].中学生数学:高中版，2009(5):3.